Курсовая работа: Энергетический и кинематический расчет привода

Курсовая работа: Энергетический и кинематический расчет привода

Содержание

Введение

1          Энергетический и кинематический расчет привода

2          Выбор материала и определение допускаемых напряжений для зубчатых передач

3          Расчет тихоходной цилиндрической зубчатой передачи.

3.1       Проектный расчет передачи

3.2       Проверочный расчет передачи на контактную выносливость.

3.3       Проверочный расчет передачи на напряжение изгиба.

3.4       Расчет геометрических параметров передачи.

3.5       Силы в зацеплении зубчатых колес.

4          Расчет промежуточной цилиндрической зубчатой передачи.

4.1       Расчет быстроходной зубчатой передачи.

5          Расчет валов.

5.1       Проектный расчет валов.

5.2       Проверочный расчет тихоходного вала редуктора.

6          Выбор подшипников качения.

6.1       Проверочный расчет подшипников тихоходного вала.

7          Расчет шпоночных соединений.

8          Выбор муфт.

9          Смазка редуктора.

10 Список использованных источников.

Введение

«Детали машин» являются курсом, в котором изучают основы проектирования машин и механизмов.

Любая машина (механизм) состоят из деталей.

Деталь – такая часть машины, которую изготавливают без сборочных операций. Они могут быть простыми и сложными. Детали объединяют в узлы.

Узел представляет собой законченую сборочную единицу, состоящую из ряда деталей, имеющих общее функциональное назначение.

Детали общего назначения применияют в машиностроении в очень больших количествах. Поэтому, любое усовершенствование методов расчета и конструкции этих деталей, уменьшают затраты материала, понижают стоимость производства, повышают долговечность, к чему и надо стремиться.

Также конструкция должна обеспечивать легкую доступность к узлам и деталям, для их осмотра и замены. Сменные детали должны быть взаимозаменяемыми с запасными частями.

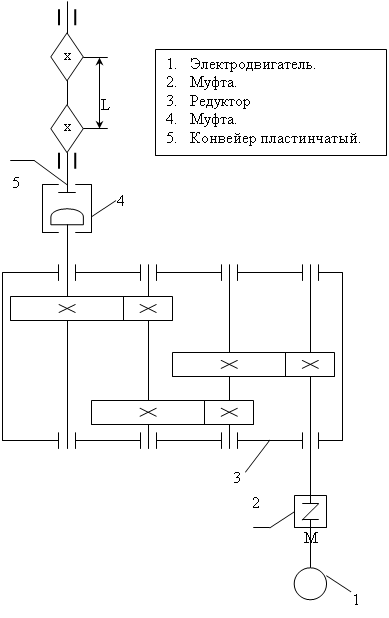
Особые указания.

1.         Редуктор и электродвигатель закреплены на общей раме.

2.         Нагрузка равномерная.

3.         Работа трехсменная.

4.         Срок службы редуктора 8 лет.

5.         Расстояние между тяговыми звездочками L принять:

L = (1,1 – 1,5)*D0;

где D0 – диметр звездочки.

6.         Ft – тяговое усилие одной цепи.

7.         P – шаг цепи.

8.         z – число зубьев звездочки.

9.         v – скорость движения конвейра.

Разработать.

1.         Общий вид привода.

2.         Редуктор.

3.         Вал со звездочками и подшипниками.

4.         Раму.

5.         Рабочие чертежи деталей.

6.        

1      Энергетический и кинематический расчет привода

Расчитаем сначала мощность, потребляемую пластинчатым конвейером по формуле:

Pб = Ft*v;        (1.1)

где:

Ft – тяговое усилие одной цепи;

v – скорость движения конвейра.

Так как у нас две звездочки, то и цепи будет две. Следовательно формула (1.1) выглядит так: Pб = 2*Ft*v = 2*4,50*0,25 = 2,25кВт.

Затем находим частоту вращения звездочек по формуле:

nб= 60000*v/D;       (1.2)

где:

v – скорость движения конвейра;

D – диаметр звездочки.

Так как D = P*z

где:

P – шаг цепи;

z – число зубъев звездочки.

Следовательно формула (1.2) выглядит следующим образом.

nб = 60000*v/P*z = 60000*0,25/100*12 = 12,5 мин-1;

После, находим необходимую мощность электродвигателя:

Рэ.д.н. = Рб/0;

где  Рб потребляемая пластинчатым конвейером мощность;

0 – общий коэффициент полезного действия привода, он равен:

0 = 5п.к. * 3зуб.п.* 2м = 0,995*0,973*0,992 = 0,85;

где п.к. – коэффициент полезного действия зубчатой прямозубой передачи.

зуб.п – коэффициент полезного дкйствия зубчатой прямозубой передачи.

м – коэффициент полезного действия муфты.

Рэ.д.н. = 2,25/0,85 = 2,65 кВт;

Далее определяем орентичовачное передаточное отношение привода:

U0 = Uб.з.п. * Uпр.з.п. * Uт.з.п. = 4*3,7*3 = 44,4  (1.3)

где Uб.з.п. – передаточное отношение быстроходной зубчатой передачи.

Uпр.з.п. – передаточное отношение промежуточной зубчатой передачи.

Uм.з.п.  - передаточное отношение тихоходной зубчатой передачи.

Определяем частоту вращения электродвигателя.

n э.д.н. = nб * U0 = 12,5 * 44,4 = 555 мин-1;

где - nб частота вращения звездочек;

U0 – передаточное отношение привода.

Выбираем двигатель типа 4А112МВ8УЗ, мощностью Р=3 кВт и частотой вращения n=665 мин-1.

Следовательно после этого уточняем общее передаточное число привода:

U0 = nэ.д./nб = 665/12,5 = 53

где nэ.д. – частота вращения двигателя;

nб – частота вращения звездочек.

Так как выражение (1.3) равняется 53, то

U0 = Uб.з.п. * Uпр.з.п. * Uт.з.п.= 4,1*3,8*3,4 = 53.

Отсюда следует, что передаточное число быстроходной ступени зубчатой передачи равно 4,1; тихоходной 3,4; промежуточной – 3,8.

После этого находим все частоты вращения валов.

n1 = nэ.д. = 665 мин-1;

n2 = n1/Uб.з.п. = 665/4,1 = 162 мин-1;

n3 = n2/Uп.з.п. = 162/3,8 = 42,6 мин-1;

n4 = n3/Uт.з.п. = 42,6/3,4 = 12,5 мин-1;

n5 = n4 = 12,5 мин-1;

Затем определим мощности на валах.

Р1 = Рэ.д. * м * п.к. = 2,65*0,99*0,99 = 2,60 кВт;

Р2 = Р1 * з.п. * п.к. = 2,60*0,97*0,99 = 2,50 кВт;

Р3 = Р2 * з.п. * п.к. = 2,50*0,97*0,99 = 2,40 кВт;

Р4 = Р3 * з.п. * п.к. = 2,40*0,97*0,99 = 2,30 кВт;

Р5 = Р4 * з.п. * п.к. = 2,30*0,97*0,99 = 2,25 кВт;

Вычеслим крутящие моменты на валах.

Т= 9559*Р/n;

где Р – мощность на валу;

n – частота вращения вала.

Т1 = 9559*Р1/n1 = 9550*2,60/665 = 37,3 Н*м;

Т2 = 9559*Р2/n2 = 9550*2,50/162 = 147,4 Н*м;

Т3 = 9559*Р3/n3 = 9550*2,40/42,6 = 538 Н*м;

Т4 = 9559*Р4/n4 = 9550*2,30/12 = 1757б2 Н*м;

Т5 = 9559*Р5/n5 = 9550*2,25/12,5 = 1719 Н*м;

Определяем угловые скорости на валах.

 = *n/30;

где n – частота вращения вала.

1 = n1/30 = 3,14*665/30 = 69,6 мин-1;

2 = n2/30 = 3,14*162/30 = 16,96 мин-1;

3 = n3/30 = 3,14*42,6/30 = 4,4 мин-1;

4 = n4/30 = 3,14*12,5/30 = 1,3 мин-1;

5 = n5/30 = 3,14*12,5/30 = 1,3 мин-1;

2          Выбор материала и определение допускаемых напряжений для зубчатых передач

Шестерни и зубчатые колеса изготавливаются из стали 40Х твердость поверхности которых менее 350, что позволяет производить чистовое нарязание зубъев после термообработки. При этом можно получать высокую точность без применения дорогих отделочных операций (шлифофки, притирки, и т.п.). Колеса этой группы хорошо прирабатываются и не подвержены хрупкому разрушению при динамических нагрузках.

Определим допускаемые напряжения для тихоходной зубчатой передачи.

Шестерня – сталь 40ХНВ250.

нр1 = 0,9*нlim1*zN1/Sн1 = 0,9*570*0,95/1,2 = 406 МПа;

где нlim – пределы контактной выносливости шестерни.

нlim1 = 2*HHB+70 = 2*250+70 = 570 МПа;

zN1 – коэффициент долговечности шестерни.

;

где Nнlim – базовое число циклов напряжений, соответствующее пределу выносливости.

Nнlim = 30* HHB2,4 = 30*2502,4 = 17067789;

Nк – расчетное число циклов напряжений при постоянном режиме нагрузки.

Nк = 60*n*c*t = 60*42,6*1*19008 = 48584448;

где n – частота вращения шестерни;

с- число колес, находящихся в зацеплении с расчитываемым;

t – число часов работы передачи за расчетный срок службы.

t = 0,33*24*8*300 = 19008 ч.

Sн1 – коэффициент запаса прочности шестерни;

Sн1=1,2 – при однородной структуре зуба.

Колесо – сталь 40HB230

нр2 = 0,9*нlim2*zN2/Sн2 = 0,9*530*1/1,2 = 397,5 МПа;

нlim2 = 2*HHB+70 = 2*230+70 = 530 МПа;

;

Nнlim = 30* HHB2,4 = 30*2302,4 = 13972305;

Nк = 60*n*c*t = 60*12,5*1*19008 = 14256000;

нр = 0,45 (нр1+нр2) < 1,23 нр min;

нр = 0,45 (406+397,5) < 1,23 * 361,6;

361,6 МПа < 444,8 МПА;

Определим допускаемые напряжения изгибы.

FP1 = Flim * YN1 * YA1 / SF1 = 437,5*0,66*0,75/1,4 = 155 МПа;

где Flim1 – пределы изгибной выносливости шестерни;

Flim1 = 1,75*HHB = 1,75*250 = 437,5 МПа;

YN1 – коэффициент долговечности;

;

  где NFG – базовое число циклов перемены напряжений

NR – расчетное число циклов, NR = NK, напряжений при постоянном режиме нагрузки;

YA1 – коэффициент, учитывающий влияние двухсторонней приложенной нагрузки;

FP2 = Flim2*YN2*YA2 / SF2 = 402,5*0,8*0,75/1,4 = 172,5 МПа;

Flim2 = 1,75*HHB = 1,75*230 = 402,5 МПа;

;

Для промежуточной зубчатой передачи.

Шестерня – сталь 40ХHB255.

нр1 = 0,9*нlim1*zN1/Sн1 = 0,9*580*0,89/1,2 = 387 МПа;

;

Nнlim = 30* HHB2,4 = 30*2552,4 = 17898543;

Nк = 60*n*c*t = 60*162*1*19008 = 184787760;

нlim1 = 2*HHB+70 = 2*255+70 = 580 МПа;

Колесо – сталь 40ХHB235.

нр2 = 0,9*нlim2*zN2/Sн2 = 0,9*540*0,94/1,2 = 381 МПа;

;

Nнlim = 30* HHB2,4 = 30*2352,4 = 14712420;

Nк = 60*n*c*t = 60*42,6*1*19008 = 48584448;

нlim1 = 2*HHB+70 = 2*235+70 = 540 МПа;

нр = 0,45 (387+381) < 1,23 * 346;

       346 МПа < 425 МПА;

Определяем допускаемые напряжения изгиба.

FP1 = Flim1*YN1*YA1 / SF1 = 446*0,53*0,7/1,4 = 118 МПа;

Flim1 = 1,75*HHB = 1,75*255 = 446 МПа;

;

FP2 = Flim2*YN2*YA2 / SF2 = 411*0,66*0,7/1,4 = 136 МПа;

Flim2 = 1,75*HHB = 1,75*235 = 411 МПа;

;

Для быстроходной зубчатой передачи.

Шестерня – сталь 40ХНВ260.

нр1 = 0,9*нlim1*zN1/Sн1 = 0,9*590*0,83/1,2 = 367 МПа;

;

Nнlim = 30* HHB2,4 = 30*2602,4 = 18752418;

Nк = 60*n*c*t = 60*665*1*19008 = 758419200;

Колесо – сталь 40ХНВ240.

нр2 = 0,9*нlim2*zN2/Sн2 = 0,9*550*0,88/1,2 = 363 МПа;

;

нlim1 = 2*HHB+70 = 2*240+70 = 550 МПа;

нр = 0,45 (367+363) < 1,23 * 328,5;

328,5 МПа < 404 МПА;

 Определяем допускаемые напряжения изгиба.

FP1 = Flim1*YN1*YA1 / SF1 = 455*0,42*0,8/1,4 = 109 МПа;

Flim1 = 1,75*HHB = 1,75*260 = 455 МПа;

;

FP2 = Flim2*YN2*YA2 / SF2 = 420*0,53*0,8/1,4 = 127 МПа;

Flim2 = 1,75*HHB = 1,75*240 = 420 МПа;

;

3          Расчет тихоходной цилиндрической зубчатой передачи

Исходные данные для расчета тихоходной цилиндрической зубчатой передачи:

N – передаваемая мощность, кВт;

N = 2,40 кВт;

n1 – частота вращения шестерни, мин-1;

n1 = 42,6 мин-1;

n20 – желаемая частота вращения колеса, мин-1;

n20 = 12,5 мин-1;

n2д – допустимое отклонение частоты вращения колеса от желаемой, мин-1;

n2д = 0,62 мин-1;

t – число часов работы передачи за расчетный срок службы;

t = 0,33*24*8*300 = 19008 ч.

3.1       Проектный расчет передачи

Расчитаем момент на шестерне по формуле:

T1 = 9550*N*к/n1 = 9550*2,40*1,3/42,6 = 699 Н*м;

где N – передаваемая мощность, кВт;

n1 – частота вращения шестерни, мин-1;

к – коэффициент нагрузки передачи, к = кv * к = 1,3;

где кv – коэффициент динамической нагрузки;

к - коэффициент, учитывающий неравномерность распределения нагрузки по ширине зубчатого венца;

Затем вычисляем предполагаемое передаточное число по формуле:

 U0 = h1/h02 = 42,6/12,5 = 3,4

где h1 – частота вращения шестерни, мин-1;

h02 – желаемая частота вращения колеса, мин-1;

Выбираем предполагаемый коэффициент ширины шестерни относительно ее начального диаметра: b0d = 0,8;

Расчитываем предполагаемое межосевое растояние по формуле:

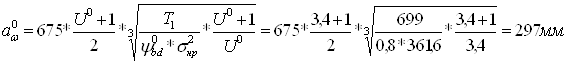г

де T1 – расчетный момент на шестерне;

U0 – предполагаемое передаточное число;

b0d – предполагаемый коэффициент ширины шестерни относительно ее начального диаметра;

нр допускаемое контактное напряжение передачи;

Выбираем желаемое межосевое расстояние.

Далее выбираем допустимое отклонение межосевого расстояния.

Значение a выбираем в пределах:

0,01* a< a < 0,1*ag;

0,01*300 < a< 0,1*300;

3 < a< 30;

Следовательно  a принимаю равным 15мм, т.к. 3<15<30.

Данное значение удовлетворяет выше приведенное условие.

Расчитываем предполагаемый начальный диаметр шестерни по формуле:

d01 = 2*ag/(U0+1) = 2*300/(3,4+1) = 136мм;

где U0 – предполагаемое передаточное число;

ag – желаемое межосевое растояние.

Вычисляем предполагаемую рабочую ширину:

b0 = b0d * d01 = 0,8*136 = 109мм.

где b0d – предполагаемый коэффициент ширины шестерни относительно ее начального диаметра;

d01 – предполагаемый начальный диаметр шестерни;

Выбираем рабочую ширину из соотношения

Она равняется 110мм

;

Выбираем число зубъев колеса из условия: z1>16;

Принимаем z1=20;

Затем вычислим число зубъев колеса по выражению:

z2=z1*U0 = 20*3,4 = 68;

где z1 – число зубъев шестерни;

U0 – предполагаемое передаточное число;

Угол наклона линии зуба =00, так как по условию задания передача циклическая, прямозубая.

Расчитываем предполагаемый модуль по формуле:

m0 = 2*ag*cos /(z1+z2) = 2*300*cos 0/(20+68) = 6,8мм;

где ag – желаемое межосевое растояние;

 - угол наклона линии зуба;

z1 – число зубъев шестерни;

z2 – число зубъев колеса;

Выбираем значение модуля по выражению m=m0 из ряда модулей СТСЭВ310-76.

;

Значение модуля равняется 7мм.

Выбираем коэффициенты смещения шестерни и колеса x1=0,5; x2=0,5 из условия, что 17<=z1<=30 и U0<3,5.

3.2       Проверочный расчет передачи на контактную выносливость

Проверочный расчет передачи на контактную выносливость производится по расчетным контактным напряжениям. Они рассчитываются по формуле:

Необходимо выполнение условия 0,7*нр <= н <= нр.

где zн – коэффициент, учитывающий форму сопряженных поверхностей зубьев в полосе зацепления, и он равен zн=2,4;

z - коэффициент, учитывающий суммарную длину контактных линий, он равен z=0,88;

t – удельная расчетная окружная сила, t=89Н/мм.

0,7*361,6 <= 357 <= 361,6;

Условие выполняется. Значит передача выдержит нагрузку.

3.3 Проеверочный расчет передачи по напряжениям изгиба

Проверочный расчет передачи по напряжения м изгиба производится по расчетным напряжениям изгиба зубъев шестерни и колеса. Они расчитываются по формулам:

F1 = YFS1*YB*Y*t/m = 3,45*1*1*89/7 = 44МПа.

где YFS1 – коэффициент, учитывающий форму зуба и концентрацию напряжений шестерни, вычисляется по формуле:

YFS1=3,47*13,2/zv1-27,9*x1/zv1+0,092*x12=3,45;

YB – коэффициент, учитывающий наклон зуба, определяется по формуле:

YB = 1-0/120 = 1-0*0/120=1;

Y - коэффициент, учитывающий перекрытие зубъев, Y=1;

t – удельная расчетная окружная сила.

Для колеса:

F2 = YFS2*YB*Y*t/m = 3,48*1*1*89/7 = 44МПа.

где YFS2 – коэффициент, учитывающий форму зуба и концентрацию напряжений колеса, вычисляется по формуле:

YFS2=3,47*13,2/zv2-27,9*x2/zv2+0,092*x22=3,48;

3.3       Расчет геометрических параметров передачи

Определяем передаточное число:

U = z2/z1 = 68/20 = 3,4;

где z1 – число зубъев шестерни;

z2 – число зубъев колеса;

Далее вычисляем сумму чисел зубъев по выражению:

z = z1+z2 = 20+68 = 88;

Определяем частоту вращения колеса по формуле:

h2 = h1/4 = 42,6/3,4 = 12,5 мин-1;

где h1 – частота вращения шестерни;

U – передаточное число.

Далее вычислим модуль отклонения частоты вращения колеса от желаемой через выражение:

h2R = |h2-h20| = |12,5-12,5| = 0;

где h2 – частота вращения колеса;

h20 – желаемая частота вращения колеса;

Необходимо, чтобы выполнилось условие h2R<h2D.

Оно выполняется, т.к. 0<0,62. Следовательно число зубъев шестерни и колеса выбраны правильно.

Затем определим торцовый угол профиля по выражению:

t = arctg(tg /cos ) = 200;

где  - угол наклона зуба;

- угол наклона линии зуба;

Вычислим угол зацепления по выражению:

inv t= 2*x*tg / z + inv t = 0,023;

где x - сумма чисел;

z - сумма коэффициентов;

Смещение определяем по выражению:

x = x1+x2=0,5+0,5=1;

где x1 – коэффициент смещения шестерни;

x2 - коэффициент смещения колеса;

Определяем межосевое расстояние a, a=314 мм.

Вычисляем модуль отклонения межосевого расстояния от желаемого по выражению:

aR = |a - ag| = |314-300| = 14 мм.

Необходимо, чтобы выполнялось условие aR <= a;

14 <= 15мм – условие выполняется.

Далее расчитываем делительный диаметр шестерни через выражение:

d1 = m*z1/cos  = 7*20/cos 0 = 140 мм;

где m – модуль;

z1 – число зубъев шестерни;

 - угол наклона линии зуба.

Затем определим делительный диаметр колеса по выражению:

d2 = m*z2/cos  = 7*68/cos 0 = 476 мм;

где m – модуль;

z2 – число зубъев колеса;

 - угол наклона линии зуба.

Вычисляем начальный диаметр шестерни, а затем начальный диаметр колеса по выражениям:

d1 = 2*a*z1/z = 2*314*20/88 = 143 мм;

d2 = 2*a*z2/z = 2*314*68/88 = 447 мм;

Определяем основной диаметр шестерни и колеса по выражениям:

db1 = d1*cos t = 140*cos 200 = 132 мм;

db2 = d2*cos t = 140*cos 200 = 132 мм;

где d1, d2 – делительный диаметр шестерни и колеса;

t – торцовый угол профиля;

Далее определяем диаметр вершин зубъев шестерни и диаметр вершин зубъев колеса по выражениям:

da1 = d1+2*m*(ha*+x1) = 140+2*7*(1+0,5) = 161 мм

da2 = d2+2*m*(ha*+x2) = 476+2*7*(1+0,5) = 497 мм

где d1, d2 – делительный диаметр шестерни и колеса;

x1, x2 – коэффициенты смещения шестерни и колеса;

Затем определяем диаметр впадин зубъев шестерни и колеса по выражениям:

df1 = d1 – 2*m*(hf* - x1) = 140-2*7(1,25-0,5) = 129 мм

df2 = d2 – 2*m*(hf* - x2) = 476-2*7(1,25-0,5) = 465 мм

Находим коэффициент наименьшего смещения шестерни xmin,     xmin = -0,2. Должно выполняться условие xmin <= x1;

-0,2 <= 0,5 – условие выполняется.

Определяем основной угол наклона по выражению:

6=arcsin(sin *cos ) = 00;

Далее находим основной окружной шаг и осевой шаг по выражениям:

P6t = *m*cos t / cos 3,14*7*cos 20/cos 0 = 21 мм;

Px = *m/ sin 3,14*7/sin 0 = 0 мм;

где m – модуль;

 - угол наклонения зуба;

t – торцовый угол профиля;

Вычисляем угол профиля зуба шестерни в точке на окружности вершин a1, a1 = 350.

Определяем угол профиля зуба колеса в точке на окружности вершин a2, a2 = 260.

Затем определяем коэффициент торцового перекрытия и коэффициент осевого перекрытия  и ,  = 1,65,  = 0.

Определим суммарную длину контактных линий по формуле:

 lm=b*/cos t = 181 мм;

Вычисляем коэффициент среднего изменения суммарной длины контактных линий по формуле:

;

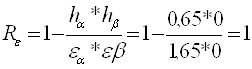Далее расчитаем наименьшую суммарную длину контактных линий по выражению: lmin = lm*R = 181*1 = 181 мм.

Необходимо выполнение условия: lmin => bмм > 110 мм.

Определяем число зубъев шестерни и колеса, охватываемых нормалемером zn1 и zn2, zn1 = 3, zn2 = 9.

Вычисляем длину общей нормали шестерни и колеса W1 и W2,

W1 = 56мм, W2 = 185мм.

3.5 Силы зацепления зубчатых колес

В зубчатых передачах действует окружная сила Ft и нормальная сила Fn, также могут действовать и другие силы.

Вычисляем окружную силу по формуле:

Ft = 2000*T1/d1 = 200*699/143 = 9776 Н.

где T1 – расчетный вращающий момент на шестерне и оси расчитывается по формуле:

T1 = 9550*1,3*N/h1 = 699 Н*м;

Далее вычисляем осевую силу, действующую на вал по формуле:

Fx = Ft*tg  = 9776*tg 0 = 0 Н;

Определяем радиальную силу по выражению:

Fr = Ft*tg t = 9776*tg 230 = 4106 Н;

4 Расчет промежуточной и быстроходной передачи

Исходные данные для расчета промежуточной передачи:

N = 2,50 кВт

n1 = 162 мин-1

n20 = 42,6 мин-1

n2D = 2,13 мин-1

t = 19008 ч.

Расчитаем моменты на шестерне по формуле:

T1 = 9550*N*k/n1 = 9550*2,50*1,3/162 = 191 Н*м;

Все разъяснения по формуле см. в предыдущем параграфе.

Выбираем предполагаемый коэффициент ширины шестерни относительно ее начального диаметра: bd0 = 0,8;

Расчитываем предполагаемое передаточное число по формуле:

U0 = n1/n20 = 162/42,6 = 3,8;

Затем расчитываем предполагаемое межосевое расстояние:

a0 = 227 мм.

Выбираем желаемое расстояние: ag  a0; 230  227мм.

Выбираем допустимое отклонение межосевого расстояния из выражения:

 0,01* ag <  a < 0,1* ag

0,01*230  < 10   <  0,1*230

2,3  < 10  <  23

Следовательно условие выполняется и  a равняется 10.

Расчитываем предполагаемый наральный диаметр шестерни по формуле:

;

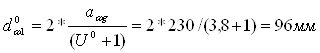Расчитаем предполагаемую рабочую ширину по формуле:

b0 = bd0*d10 = 0,8 * 96 = 77 мм;

Рабочую ширину выбираем из условия: b  b0; 78  77 мм.

Рабочая ширина составляет 78 мм.

Выбираем число зубъев шестерни из условия z1>16, z1=20;

Расчитаем число зубъев колеса по выражению: z2 z1*U0  76

Угол наклона линии зуба  = 0.

Расчитаем преполагаемый модуль m0, m0 = 4,8 мм.

Выбираем значение модуля из выражения m  m0 , 5  4,8 мм.

Модуль равняется 5 мм.

Выбираем коэффициент смещения шестерни и колеса из условия, что 17 <=z1<= 20 и U0=>3,5; следовательно x1=0,3; x2=-0,3.

Далее расчитываем геометрические параметры передачи:

1.   Передаточное число U; U = z2/z1 = 76/20 = 3,8;

2.   Сумма чисел зубъев z; z= z1 + z2 = 20+76 = 96;

3.   Частота вращения колеса h2=h1/U = 162/3,8 = 42,6 мин-1;

4.   Модуль отклонения частоты вращения колеса от желаемой h2R=|h2 – h20| = |42,6 – 42,6| = 0;

5.   Торцовый угол профиля t = arctg(tg /cos ) = 200;

6.   Сумма коэффициентов смещений x= x1+x2 = 0,3+(-0,3) = 0;

7.   Угол зацепления t = t = 200; при x= 0;

8.   Межосевое расстояние  = 240 мм;

9.   Модуль отклонения межосевого расстояния от желаемого aR = |a - ag| = |240-230| = 10 мм;

10.       Делительный диаметр шестерни d1= m*z1/cos  = 5*20/cos 00 = 100мм;

11.       Делительный диаметр колеса d2 = m*z2/cos  = 5*76/cos 00 = 380 мм;

12.       Начальный диаметр шестерни d1 = 2*a*z1/z = 2*240*20/96 = 100 мм;

13.       Начальный диаметр колеса d2 = 2*a*z2/z = 2*240*76/96 = 380 мм;

14.       Основной диаметр шестерни db1 = d1*cos t = 100*cos 200 = 94 мм;

15.       Основной диаметр колеса db2 = d2*cos t = 380*cos 200 = 357 мм;

16.       Диаметр вершин зубъев шестерни da1 = d1+2*m*(ha*+x1) = 100+2*5*(1+0,3) = 113 мм;

17.       Диаметр вершин зубъев колеса da2 = d2+2*m*(ha*+x2) = 380+2*5*(1+0,3) = 387 мм;

18.       Диаметр впадин зубъев шестерни df1 = d1-2*m*(hf*-x1) = 100-2*5*(1,25-0,3) = 90 мм;

19.       Диаметр впадин зубъев колеса df2 = d2-2*m*(hf*-x2) = 380-2*5*(1,25-0,3) = 364 мм;

Коэффициент наименьшего сцепления шестерни xmin = -0,2;

xmin < x1

-0,2 < 0,3;

Основной угол наклона t = 00;

Основной окружной шаг Pbt = 15мм;

Осевой шаг Px = 0мм;

Угол профиля зуба шестерни и зуба колеса в точке по окружности вершин

a1 = arccos (db1/da1) = 340;

a2 = arccos (db2/da2) = 230;

Коэффициент торцового перекрытия

 = (z1*tga1+z2*tga2 z*tg2t) / (2*) = 1,7;

 Коэффициент осевого перекрытия

 = b/Px = 78/0 = 0;

Коэффициент перекрытия

v =  +  = 1,7 + 0 = 1,7;

Средняя суммарная длина контактных линий lm  133 мм.

Коэффициент среднего изменения суммарной длины контактных линий R = 1;

Наименьшая суммарная длина контактных линий

lmin = lm * R = 133мм;

lmin => b

133 > 78;

Число зубъев шестерни и колеса охватываемых нормалемером:

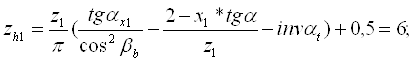
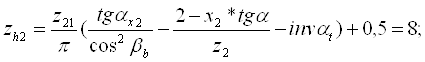
Длина общей нормалишестерни и колеса:

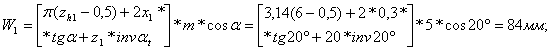
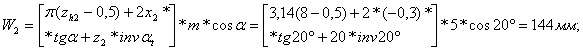
Далее рассчитываем силы в зацеплении зубчатых колес.

Рассчитаем вращающий момент

T1 = 9550*1,3*N/n1 = 9550*1,3*2,5/162 = 191 H*м;

Расчетный вращающий момент на колесе

T2 = T1*U* = 191-3,8*0,97 = 704 Н*м;

Расчетная окружная сила

Ft = 2000*T1/d1 = 2000*191/100 = 3820 H;

Расчетная радиальная сила

Fr = Ft*tg t = 3820*tg200 = 1375 H;

Расчетная осевая сила

Fx = Ft*tg 3820*tg 00 = 0 H;

Расчетная нормальная сила

Fn = Ft/(cos t*cos b) = 4064 H;

Затем провожу проверочный расчет передачи на контактную выносливость и на напряжения изгиба.

Удельная расчетная окружная сила

t = Ft/6H/м;

Коэффициент, учитывающий форму сопряженных поверхностей зубъев в полосе зацепления: zH = 2,5;

Коэффициент, учитывающий суммарную длину контактных линий: z = 0,87 для  = 0;

Расчетные контактные напряжения:

H = 326 мПа;

0,7*Hp <= H <= Hp; 0,7*346 <= H <= 346;

242 <= 326 <= 346;

Эквивалентное число зубъев шестерни: zv1 = z1/cos3 = 20; Эквивалентное число зубъев колеса: zv2 = z2/cos3 = 76;

Коэффициент, учитывающий форму зуба и концентрацию напряжений шестерни:

YFS1 = 3,47*13,2/zv1–27,9*x1/zv1+0,092x12 = 3,7;

Коэффициент, учитывающий форму зуба и концентрацию напряжений колеса:

YFS2 = 3,47*13,2/zv2–27,9*x2/zv2+0,092x22 = 3,8;

Коэффициент, учитывающий наклон зуба:

Y = 1-*0/120 = 1-00*00/1200 = 1;

Коэффициент, учитывающий перекрытие зубъев Y

Расчетные напряжения изгиба зубъев шестерни F1 = 36 мПа;

0,25*Fp1 <= F1 <= Fp1;

0,25*Fp1 <= 36 < = Fp1;

0,25*118 < = 36 < = 118;

29,5 <= 36 < = 118;

Расчетные напряжения изгиба зубъев колеса F2 = 37 мПа;

0,25*Fp1 <= F1 <= Fp1;

0,25*Fp1 <= 37 < = Fp1;

0,25*136 < = 37 < = 136;

34 <= 37 < = 136;

Данная передача будет работать нормально, так как выполняются все данные условия.

4.1 Расчет быстроходной цилиндрической передачи

Исходные данные для расчета быстроходной передачи:

N = 2,60 кВт;

h1 = 665 мин-1;

h20 = 162 мин-1;

h2D = 8,1 мин-1;

t = 19008 ч.

Расчитываю момент на шестерне по формуле:

T1 = 9550*N*k/h1 = 9550*2,60*1,3/665 = 48 Н*м;

где k – коэффициент нагрузки передачи;

Вычисляем предполагаемое передаточное число по выражению

U0 = h1/h20 = 665/162 = 4,1;

Выбираем коэффициент ширины шестерни относительно ее начального диаметра bd0, bd0 = 0,8;

Затем расчитываем предполагаемое межосевое расстояние a0 = 154,9 мм;

Выбираем желаемое межосевое расстояние из условия:

 0,01* ag <  a < 0,1* ag

0,01*155  < 5   <  0,1*155

1,55  < 5  <  15,5

Следовательно условие выполняется и  a равняется 5мм.

Расчитываем предполагаемый наральный диаметр шестерни по формуле:

;

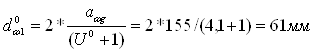Расчитаем предполагаемую рабочую ширину по формуле:

b0 = bd0*d10 = 0,8 * 61 = 49 мм;

Рабочую ширину выбираем из условия: b  b0; 56  49 мм.

Выбираем число зубъев шестерни из условия z1>16, z1=20;

Расчитаем число зубъев колеса по выражению: z2 z1*U0  82

Угол наклона линии зуба  = 0.

Расчитаем преполагаемый модуль m0, m0 = 3,04 мм.

Выбираем значение модуля из выражения m  m0 , 3  3,04 мм.

Модуль равняется m=5 мм. (по СТСЭВ 310-76)

Выбираем коэффициент смещения шестерни и колеса x1=0,3; x2=-0,3.

Далее расчитываем геометрические параметры передачи:

1.   Передаточное число U; U = z2/z1 = 82/20 = 4,1;

2.   Сумма чисел зубъев z; z= z1 + z2 = 20+82 = 102;

3.   Частота вращения колеса h2=h1/U = 665/4,1 = 126 мин-1;

4.   Модуль отклонения частоты вращения колеса от желаемой h2R=|h2 – h20| = |162 – 162| = 0;

5.   Торцовый угол профиля t = arctg(tg /cos ) = 200;

6.   Сумма коэффициентов смещений x= x1+x2 = 0,3+(-0,3) = 0;

Угол зацепления t = t = 200; при x= 0;

7.   Межосевое расстояние  = 153 мм;

8.   Модуль отклонения межосевого расстояния от желаемого aR = |a - ag| = |153-155| = 2 мм;

9.   Делительный диаметр шестерни d1= m*z1/cos  = 3*20/cos 00 = 60мм;

10.       Делительный диаметр колеса d2 = m*z2/cos  = 3*82/cos 00 = 246 мм;

11.       Начальный диаметр шестерни d1 = 2*a*z1/z = 2*153*20/102 = 60 мм;

12.       Начальный диаметр колеса d2 = 2*a*z2/z = 2*153*82/102 = 246 мм;

13.       Основной диаметр шестерни db1 = d1*cos t = 60*cos 200 = 56 мм;

14.       Основной диаметр колеса db2 = d2*cos t = 246*cos 200 = 231 мм;

15.       Диаметр вершин зубъев шестерни da1 = d1+2*m*(ha*+x1) = 60+2*3*(1+0,3) = 68 мм;

16.       Диаметр вершин зубъев колеса da2 = d2+2*m*(ha*+x2) = 246+2*3*(1+0,3) = 250 мм;

17.       Диаметр впадин зубъев шестерни df1 = d1-2*m*(hf*-x1) = 60-2*3*(1,25-0,3) = 54 мм;

18.       Диаметр впадин зубъев колеса df2 = d2-2*m*(hf*-x2) = 246-2*3*(1,25-(-0,3)) = 237 мм;

19.Коэффициент наименьшего смещения шестерни xmin = -0,2;

xmin < x1-0,2 < 0,3;

20.Основной угол наклона t = 00;

21.Основной окружной шаг Pbt = 9мм;

22.Осевой шаг Px = 0мм;

23.Угол профиля зуба шестерни и зуба колеса в точке по окружности вершин:

a1 = arccos (db1/da1) = 340;

a2 = arccos (db2/da2) = 220;

24.Коэффициент торцового перекрытия  = (z1*tga1+z2*tga2 z*tg2t) / (2*) = 1,5;

25.Коэффициент осевого перекрытия  = 6/Px = 56/0 = 0;

26.Коэффициент перекрытия v =  +  = 1,5 + 0 = 1,5;

27.Средняя суммарная длина контактных линий lm  84 мм.

28.Коэффициент среднего изменения суммарной длины контактных линий R = 1;

29.Наименьшая суммарная длина контактных линий

lmin = lm * R = 84мм;

lmin => b

84 > 56;

30.Число зубъев шестерни и колеса охватываемых нормалемером:

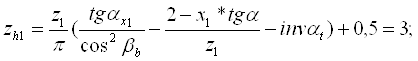
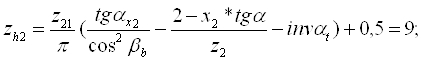
31.Длина общей нормалишестерни и колеса:

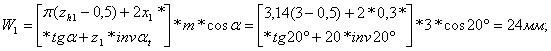
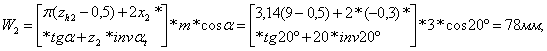
Далее рассчитываем силы в зацеплении зубчатых колес.

Рассчитаем вращающий момент T1 = 9550*1,3*N/n1 = 9550*1,3*2,6/665 = 48 H*м;

Расчетный вращающий момент на колесе T2 = T1*U* = 48*4,1*0,97 = 191 Н*м;

Расчетная окружная сила Ft = 2000*T1/d1 = 2000*48/60 = 1600 H;

Расчетная радиальная сила Fr = Ft*tg t = 1600*tg200 = 576 H;

Расчетная осевая сила Fx = Ft*tg 0*tg 00 = 0 H;

Расчетная нормальная сила Fn = Ft/(cos t*cos b) = 1702 H;

Затем провожу проверочный расчет передачи на контактную выносливость и на напряжения изгиба.

Удельная расчетная окружная сила t = Ft/6H/м;

Коэффициент, учитывающий форму сопряженных поверхностей зубъев в полосе зацепления: zH = 2,5;

Коэффициент, учитывающий суммарную длину контактных линий: z = 0,9 для  = 0;

Расчетные контактные напряжения: H = 325 мПа;

0,7*Hp <= H <= Hp; 0,7*328,5 <= H <= 328,5;

328,5 <= 325 <= 328,5;

Эквивалентное число зубъев шестерни: zv1 = z1/cos3 = 20; Эквивалентное число зубъев колеса: zv2 = z2/cos3 = 82;

Коэффициент, учитывающий форму зуба и концентрацию напряжений шестерни:

YFS1 = 3,47*13,2/zv1–27,9*x1/zv1+0,092x12 = 3,7;

Коэффициент, учитывающий форму зуба и концентрацию напряжений колеса:

YFS2 = 3,47*13,2/zv2–27,9*x2/zv2+0,092x22 = 3,8;

Коэффициент, учитывающий наклон зуба:

Y = 1-*0/120 = 1-00*00/1200 = 1;

Коэффициент, учитывающий перекрытие зубъев Y

Расчетные напряжения изгиба зубъев шестерни F1 = 34 мПа;

0,25*Fp1 <= F1 <= Fp1;

0,25*Fp1 <= 34 < = Fp1;

0,25*109 < = 34 < = 109;

27 <= 34 < = 109;

Расчетные напряжения изгиба зубъев колеса F2 = 35 мПа;

0,25*Fp1 <= F1 <= Fp1;

0,25*Fp1 <= 35 < = Fp1;

0,25*127 < = 35 < = 127;

32 <= 35 < = 127;

Данная передача будет работать нормально, так как выполняются все приведенные выше условия.

5 Расчет валов

Исходные данные для расчета валов:

Тихоходная передача:

T1 – вращающий момент на шестерне. T1 = 669 Н*м;

U – передаточное число. U = 3,4.

h2 – частота вращения колеса, h2 = 12,5 мин-1;

Ft – тяговое усилие одной цепи. Ft = 4,50 кН;

t – число часов работы передачи за расчетный срок службы.

t = 19008 ч.

0;

Промежуточная передача:

T1 = 191 Н*м;

U = 3,8;

T = 19008 ч;

h2 = 42,6 мин-1;

Ft – 4,50 кН;

0;

Быстоходная передача:

T1 = 48 Н*м;

U = 4,1;

T = 19008 ч;

h2 = 162 мин-1;

Ft – 4,50 кН;

0.

5.1 Проектный расчет валов

Все валы выполнены из материала: Сталь 45;

b = 750 мПа; T = 450 мПа;

На выходном конце вала установлена зубчатая муфта, а на входном конце установлена упругая втулочно кольцевая муфта.

Допускается 2-ух кратная перегрузка: крутящий момент и радиальная сила действующая на вале:

T2 = T1*U*з.п.*п.к. = 699*3,4*0,97*0,99 = 2282 Н*м;

Fr = 2*Ft*tg /cos  = 4500*tg 200/cos 00 = 1620 Н;

Радиальная нагрузка от муфты на выходном конце вала, с.263 [1]; FH = 5975 H;

Определяю средний диаметр вала, ф.15.1 [1]; d = 91 мм;

Устанавливаю размеры вала.

Диаметр в месте посадки колеса dk = 95 мм;

Диаметр в месте посадки втулки db = 90 мм;

Диаметр в месте посадки подшипников dп = 90-5 = 85 мм;

Диаметр в месте посадки муфты dм = 85 – 5 = 80 мм;

Расчет был произведен для вала тихоходной передачи.

Расчитываем промежуточный вал.

Допускается 2-ух кратная перегрузка: крутящий момент и радиальная сила, действующая на вал.

T2 = T1*U*з.п.*п.к. = 191*3,8*0,97*0,99 = 700 Н*м;

Fr = 2*Ft*tg /cos  = 4500*tg 200/cos 00 = 1620 Н;

Определяю средний диаметр вала, ф.15.1 [1]; d = 70 мм;

Устанавливаю размеры вала.

Диаметр в месте посадки колеса dk = 80 мм;

Диаметр в месте посадки подшипников dп = 80-5 = 75 мм;

Расчитаем вал быстроходной передачи.

Допускается 2-ух кратная перегрузка: крутящий момент и радиальная сила действующая на вале:

T2 = T1*U*з.п.*п.к. = 48*4,1*0,97*0,99 = 189 Н*м;

Fr = 2*Ft*tg /cos  = 4500*tg 200/cos 00 = 1620 Н;

Определяю средний диаметр вала; d = 43 мм;

Устанавливаю размеры вала.

Диаметр в месте посадки колеса dk = 50 мм;

Диаметр в месте посадки подшипников dп = 50-5 = 45 мм;

Входной вал не расчитывается. Диаметр вала принимаем равным 40мм.

Диаметр посадки подшибников dп = 40 – 5 = 35 мм.

Диаметр в месте посадки муфты равен диаметру вала электродвигателя 4А112МВ8УЗ, тоесть равен 32мм.

5.2 Проверочный расчет тихоходного вала редуктора

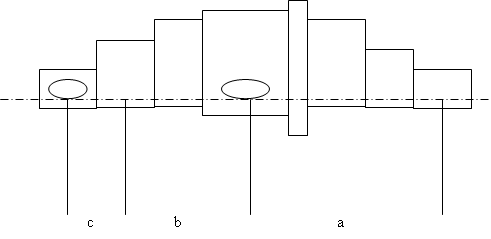
Все расстояния возьмем с чертежа. Они показаны на рис.5.2.1.

			Рис.5.2.1.

Расстояние между подшипниками (средними их плоскостями) l = 324 мм.

Расстояние между средними плоскостями зубчатого колеса и подшипников: a = 199мм; b = 125мм.

Расстояние между средними плоскостями подшипника и муфты с = 85мм.

Определим реакции в опорах и строим эпюры изгибающих и крутящих моментов.

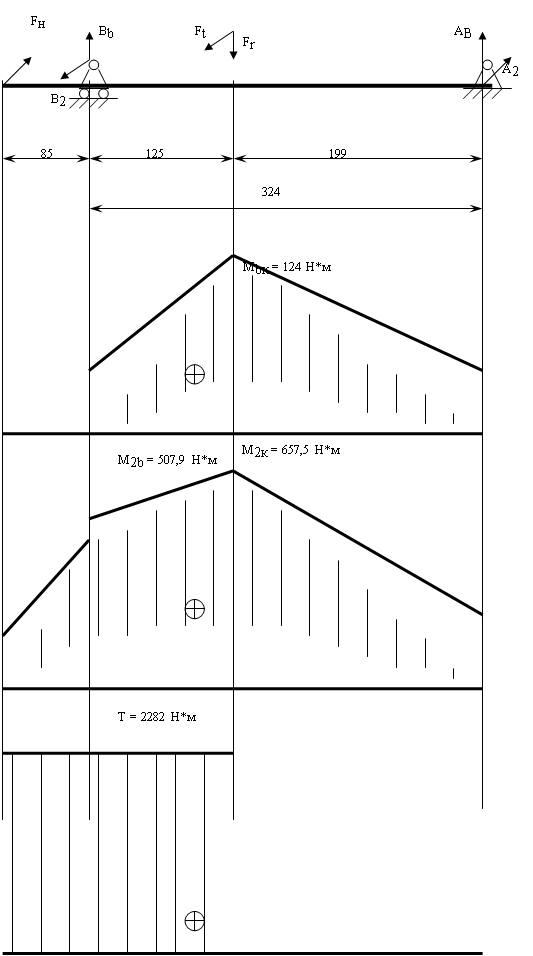
Найдем реакции от силы Fp, действующей в вертикальной плоскости.

Fr*125 Ab*324 = 0;

Ab = Fr*125/324 = 1620*125/324 = 625Н;

Ab * Bb – Fr = 0

Bb = Fr – Ab = 1620 – 625 = 995Н;

Максимальный изгибающий момент в вертикальной плоскости в месте посадки колеса:

Mbk = Ab*0,199 = 625*0,199 = 124 Н*м;

Определяем реакции от сил Ft и Fм действующих в горизонтальной плоскости:

Fм*85+Ft*125 – A2*324 = 0;

Отсюда выразим A2

A2 = (Fм*85+Ft*125)/324 = (5975*85 + 4500*125)/324 = 3304 Н;

Fм – B2 – Ft + Ar = 0;

B2 = Fм - Ft + A2 = 5975-4500+3304 = 4779 Н;

Изгибающий момент в горизонтальной плоскости над опорой B:

 Mrb = Fm*85 = 5975*85 = 507875 Н*мм = 507,9 Н*м;

Изгибающий момент в месте посадки колеса:

Mrk = Ar*199 = 3304*199 = 657496 Н*мм = 657,5 Н*м;

Крутящий момент T = T2 = 2282 Н*м;

Определяем запасы сопротивления усталости в опасных сечениях:

а) Сечение над колесом ослабленное шпоночным пазом;

б) Сечение рядом с подшипником (опора В) ослабленной

Напряжения изгиба:

nk = Mk/Wnk = Mk/(0,1*dk3) = 831/(0,1*0,0953) = 9,6 мПа;

k = T/Wp = T/(0,2*dk3) = 2282/(0,2*0,0953) = 13,3 мПа;

Пределы выносливости, ф.15.7[1]:

-1 = 0,4*b = 0,4*750 = 300 мПа;

Пределы изгиба:

-1 = 0,2*b = 0,2*750 = 150 мПа;

Эффективные коэффициенты при концентрации, соответственно при изгибе и кручении, табл.15[1]:

kk = 1,7, kk = 1,4;

Фактор шерховатости поверхности рис.15.6[1]; kF = 1;

Амплитуды соответственно нерешенных составляющих циклов напряжений, ф.15.5[1]:

ak = Hk = 9,6 мПа;

mk = 0;

ak = mk = 0,5*k = 0,5*13,3 = 6,6 мПа;

Коэффициенты, корректирующие влияние постоянной составляющей цикла напряжений на сопротивление усталости, ф.15.6[1]:  = 0,1;  = 0,05;

Запас сопротивления усталости по изгибу, ф.15.4[1]:

;

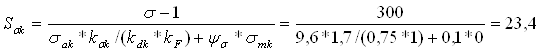Запас сопротивления устойчивости по кручению, ф.15.4[1]:

;

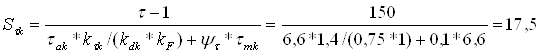Запас сопротивления усталости, ф.15.3[1]:

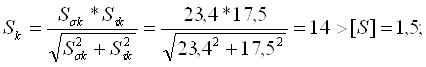
Для второго сечения определяемого необходимые параметры по соответствующим выше изложенным формулам:

nk = Mk/Wnk = Mk/(0,1*dk3) = 507,9/(0,1*0,0853) = 8,3 мПа;

b = T/Wp = T/(0,2*dk3) = 2282/(0,2*0,0853) = 18,6 мПа;

ak = nb = 8,3 мПа;

mk = 0;

ak = mk = 0,5*b = 0,5*18,6 = 9,3 мПа;

Sb = 16;

S = 14;

Sb = 10,5 > [S] = 1,5;

Второе сечение является более напряженным.

Проверим статическую прочность вала при перегрузках, напряжение удвоим, для второго сечения:

u = 2*ub = 2*8,3 = 16,6 мПа;

 = 2*b = 2*18,6 = 37,2 мПа;

[] = 0,8*T = 0,8*450 – 360 мПа;

Статические напряжения при нагрузках, ф.15.8[1]:

Условия прочности соблюдаются, диаметры вала можно сохранить.

6 Выбор подшипников качения

Для ранее расчитанных валов назначаем шариковые радиальные подшипники легкой серии, так как все передачи прямозубые.

Тихоходный вал подшипник №217, d = 85мм, D = 150мм,

B = 28мм, r = 3мм, С = 83200Н, С0 = 53000Н;

где С – диаметрическая грузоподъемность;

С0 статическая грузоподъемность.

Промежуточный вал подшипник №215, d = 75мм, D = 130мм, B = 25мм, r = 2,5мм, С = 66300Н, С0 = 41000Н.

Быстроходный вал подшипник №209, d = 45мм, D = 85мм, B = 19мм, r = 2мм, С = 33200Н, С0 = 18600Н.

Входной вал – подшипник 207, d = 35мм, D = 72мм, B = 17мм, r = 2мм, С = 25500Н, С0 = 13700Н.

6.1 Проверочный расчет подшипников тихоходного вала

Определяем реакции опор, где насаживается подшипник №217:

Выполняем расчет подшипника в опоре В, так как она более нагружена.

Эквивалентная динамическая нагрузка, ф.16.23[1].

Pr = (x*V*Frb+Y*Fa)*k*k = 5369H.

Ресурс подшипника в миллион оборотов, ф.16.21[1].

L = (C/Pr)p = (83200/5369)3 = 3721 мл.об.

Ресурс в часах, ф.16.22[1].

Ln = 106*L/(60*n2) = 106*3721/(60*12,5) = 4,96*106ч > 5000ч.

Условие выполняется.

Проверим подшипник на статической грузоподъемности.

Эквивалентная статическая нагрузка, ф.16.29[1].

P0 = X0*FrB+Y0*Fa = 0,6*4881+0,5*0 = 2929H < C0 = 53000H.

Условие выполняется, следовательно подшипник выбран правильно.

7 Расчет шпоночных соединений

На всех валах колеса закреплены шпонками. Шпонки призматические изготавливают из стальных прутков углеродистой или легированной стали с пределом прочности b не ниже 500 мПа.

[см] = 80…150 мПа.

На входном валу см = 4T/(h*lp*d)<=[см], где ставится муфта.

см = 4*37,3/(8*38*32)<= [см];

см = 15 мПа<=[см] = 90 мПа;

 2T/(6*lp*d)<=[

2*37,3/(10*38*32) = 6 мПа<= [] = 70 мПа.

Принимаем шпонку сечением 10Х8 и длиной равной 40мм.

На выходном вале, где сравнивается муфта:

см = 4*1757,2/(14*66*80) = 9,5 мПа <= [см] = 90 мПа;

2*1757б2/(22*66*80) = 3 мПа<= [] = 70 мПа.

Принимаем шпонку сечением 22Х14 и длиной равной 70мм.

На тихоходном валу.

см = 4*1757,2/(14*86*95) = 6 мПа <= [см] = 90 мПа;

2*1757б2/(25*68*95) = 1,7 мПа<= [] = 70 мПа.

Принимаем шпонку сечением 25Х14 и длиной равной 90мм.

Шпонки на промежуточном и быстроходном вале расчитаны на ЭВМ.

8 Выбор муфт

Для соединения отдельных узлов и механизмов в единую кинематическую цепь используются муфты, различные типы которых могут также обеспечить компенсацию смещений соединяемых валов, улучшение динамических характеристик привода, ограничение передаваемого момента, включение отдельных частей привода.

Выбор муфты производится в зависимости от диаметра вала и передаваемого крутящего момента

Tрасч. = k*Tдл. <= Tтабл.;

Tрасч. = 1*1757,2 <= Tтабл.;

1757,2 <= 16000 Н*м.

Выбираем зубчатую муфту, которая устанавливается на конце тихоходного вала.

d = 80 мм, A = 125 мм, D1 = 175 мм, D = 230 мм, D2 = 115 мм,

l = 130 мм, L = 270 мм, B = 50 мм.

Достоинство этой муфты в том, что она имеет высокую нагрузочную способность, технологичность и возможность использования в широком диапазоне условных скоростей и передаваемых моментов.

На конце входного вала, перед редуктором, ставим упругую втулочно-пальцевую муфту.

d = 32, T = 250 Н*м, D = 140 мм, L = 165 мм, l = 80 мм.

Tрасч. = 1*37,3 <= Tтабл.

37,3 <= 250 Н*м.

Данная муфта позволяет аммортизировать толчки и удары, разгрузить отдельные элементы привода от переодически изменяющихся возмущающих моментов, а также допускает некоторые радиальные и угловые смещения валов.

Условия выше приведенные выполняются, следовательно муфты выбраны правильно.

9 Смазка редуктора

Для смазки редуктора применяется авиационное масло типа МС-20, которое через горловину заливается в нижнюю часть корпуса. Подшипники смазываются так называемым масленным туманом, тоесть за счет разбрызгивания масленных капель.

В данный редуктор заливают около трех литров масла.

За уровнем масла следят при помощи маслоуказателя.

10 Список исполльзованных источников

1.         Иванов М.И. «Детали машин», учебник для машиностроительных вузов – 4с. из перераб – М. Высшая школа, 1984 г, 336с.

2.         ГОСТ 21354-75. Передачи зубчатые, цилиндрические, эвольвентные.

3.         Анурьев В.И. Справочник конструктора машиностроителя. В – 3 – х т. Т 2 – 5-е издание. перераб и доп. – М. Машиностроение, 1980 г, 559с.