
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Курсовая работа: Кінематичний аналіз плоских важільних, кулачкових і зубчастих механізмів
Курсовая работа: Кінематичний аналіз плоских важільних, кулачкових і зубчастих механізмів
Курсова робота
"Кінематичний аналіз плоских важільних, важільних, кулачкових і зубчастих механізмів"
Вступ
Ключові слова: механізм; машина; структурна група; кінематична пара; ланка; план швидкостей; план прискорень; сила.
Ціль курсового проекту: придбання практичних навичок по кінематичному аналізу й синтезу плоских важільних, важільних, кулачкових і зубчастих механізмів.
Методи проведення досліджень: аналітичний, графічний і графоаналітичний.
У даному проекті визначені структурні кінематичні й динамічні характеристики важільного механізму, спроектовані кулачковий і зубчастий механізми по заданих умовах.
1. Структурний аналіз механізму
Число ступенів волі механізму визначаємо по формулі П.Л. Чебишева.
![]()
де n число рухливих ланок механізму,
p5 число кінематичних пар п'ятого класу,
p4 число Кінематичних пар четвертого класу.
У досліджуваному механізмі n=5, p5=7, p4=0, тобто
![]()
Отже, досліджуваний механізм має одна початкова ланка, і все ланки роблять цілком певні рухи.
Визначаємо клас механізму. Клас механізму визначається вищим класом групи Ассура, що входить до складу механізму. Визначення груп починаємо із самої вилученої від початкової ланки (кривошипа). Відокремлюємо гр. А. другого класу другого виду з ланками 2 і 3.
![]()

![]()
![]() A
A
![]() 2
2
Потім відокремлюємо групу другого класу другого виду з ланками 4 і 5.
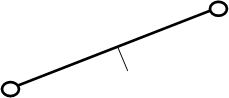
![]()
![]()
У результат розподілу залишається механізм першого класу, до складу якого входить початкова ланка 1 і стійка 0.
![]() A
A
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() O
1
O
1
Формула будови механізму має вигляд
I (0; 1) II (2; 3)
II (4; 5)
Таким чином, даний механізм ставиться до II класу.
2. Кінематичне дослідження механізму
2.1 Побудова плану положень механізму
План положень механізму є основою для побудови кінематичних діаграм лінійного переміщення повзуну, або кутового переміщення вихідної ланки. Побудова плану положень механізму виконується в масштабі ml.
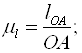
![]()
![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]() .
.
![]()
![]()
![]()
![]()
![]()
Вибираємо
ml![]() м/мм. У цьому масштабному
коефіцієнті робиться креслення кінематична схема механізму. На траєктор
крапки В повзуна 3 знаходимо її крайні положення. Крапки В0 і В6
будуть крайніми положеннями повзуну 3. За нульове положення механізму приймаємо
крайнє ліве положення, а обертання кривошипа – за годинниковою стрілкою.
Починаючи від нульового положення кривошипа ділимо траєкторію крапки A на 12
рівних частин і методом зарубок знаходимо всі інші положення ланок механізму.
Для кожного положення механізму знаходимо положення центрів мас S2
S4, з'єднавши послідовно крапки S у всіх положеннях ланок плавно
кривої, одержимо шатунні криві.
м/мм. У цьому масштабному
коефіцієнті робиться креслення кінематична схема механізму. На траєктор
крапки В повзуна 3 знаходимо її крайні положення. Крапки В0 і В6
будуть крайніми положеннями повзуну 3. За нульове положення механізму приймаємо
крайнє ліве положення, а обертання кривошипа – за годинниковою стрілкою.
Починаючи від нульового положення кривошипа ділимо траєкторію крапки A на 12
рівних частин і методом зарубок знаходимо всі інші положення ланок механізму.
Для кожного положення механізму знаходимо положення центрів мас S2
S4, з'єднавши послідовно крапки S у всіх положеннях ланок плавно
кривої, одержимо шатунні криві.
2.2 Побудова планів швидкостей
Визначення швидкостей, зазначених на кінематичній схемі крапок ланок механізму робимо методом планів у послідовності, певною формулою будови механізму. Спочатку визначаємо лінійну швидкість провідних крапок А и С.
VA=
w1× lOA= ![]() × lOA
× lOA
VС=
w1× lOC= ![]() × lOС
× lOС
де w1 - кутова швидкість початкової ланки ОА;
n1 частота обертання початкової ланки ОА;
lOA довжина ланки ОА, м;
w1= ![]()
VA=
VС = ![]()
Швидкост крапок А и B буде однаковими для всіх положень механізму. Масштабний коефіцієнт плану швидкостей вибираємо стандартним. У розглянутому прикладі
![]()
![]()
Вектор
![]() перпендикулярний кривошипу
ОА й спрямований убік його обертання.
перпендикулярний кривошипу
ОА й спрямований убік його обертання.
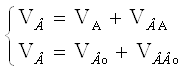
Відповідно до першого рівняння, через крапку а на плані швидкостей проводимо пряму, перпендикулярну АВ, а відповідно до другого – через крапку р проводимо пряму, паралельну напрямної X–X. Перетинання цих прямих визначає положення крапки c, що зображує кінець вектора VВ і V В. Із плану швидкостей маємо
VВ=
VВВo= (pb).![]()
![]() = 33,5 × 0,4
= 13,4 м/c
= 33,5 × 0,4
= 13,4 м/c
V В=
(ab).![]()
![]() = 45 × 0,4 = 18 м/с
= 45 × 0,4 = 18 м/с
Швидкість центра мас S2 ланки 2 визначимо по теоремі подоби:
![]() ,
,
звідки
![]()
Отже,
![]()
Швидкост крапок, що належать групі Ассура з ланками 2,3 визначені.
Переходимо
до побудови плану швидкостей для групи 4,5. Розглянемо рух крапки D щодо крапки
З, а потім стосовно крапки D0, що належить нерухливої напрямної (![]() ). Запишемо два векторних
рівняння, які вирішимо графічно:
). Запишемо два векторних
рівняння, які вирішимо графічно:
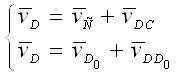
Відповідно до першого рівняння через крапку із плану швидкостей проводимо пряму, перпендикулярну до DС, а для рішення другого рівняння необхідно через полюс p провести пряму, паралельну напрямної X–X. На перетинанні цих прямих і буде перебувати шукана крапка d.
Величини
швидкостей визначимо, множачи довжини векторів на плані швидкостей на
масштабний коефіцієнт ![]()
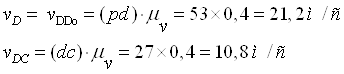
Швидкість центра мас S4 ланки 4 визначимо по теоремі подоби
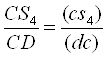 ,
,
звідки
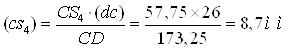
Отже,
![]()
У зазначеній послідовності виробляється побудова планів швидкостей для всіх 12-ти положень механізму. Причому, вектори, що виходять із полюса P, зображують абсолютні швидкості, а відрізки з'єднуючі кінці цих векторів – відносн швидкості крапок.
Обчислен в такий спосіб величини швидкостей зводимо в таблицю 2.1.
Визначимо кутові швидкості ланок
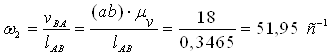
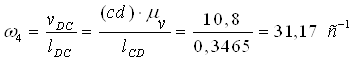
![]()
Напрямок
кутової швидкості ланки AВ визначиться, якщо перенести вектор ![]() швидкості крапки B на
схемі механізму й установити напрямок обертання ланки AB щодо крапки А під дією
цього вектора. У розглянутому випадку в положенні 1 механізму кутова швидкість
швидкості крапки B на
схемі механізму й установити напрямок обертання ланки AB щодо крапки А під дією
цього вектора. У розглянутому випадку в положенні 1 механізму кутова швидкість ![]() спрямована проти
годинникової стрілки.
спрямована проти
годинникової стрілки.
Напрямок
кутової швидкості шатуна 4 визначає вектор ![]() ,
якщо його перенести із плану швидкостей у крапку D на схемі механізму. У
положенні 1 кутова швидкість
,
якщо його перенести із плану швидкостей у крапку D на схемі механізму. У
положенні 1 кутова швидкість ![]() спрямована
проти годинникової стрілки.
спрямована
проти годинникової стрілки.
Таблиця 2.1
| № |
VО |
VА |
VB |
VS2 |
VС |
VD |
VS4 |
VВА |
VDС |
ω1 |
ω2 |
ω4 |
| м/з |
с-1 |
|||||||||||
| 0 | 0 | 20,8 | 0 | 14 | 20,8 | 20,8 | 20,8 | 20,8 | 0 | 188,4 | 60,03 | 0 |
| 1 | 0 | 20,8 | 13,4 | 16,6 | 20,8 | 21,2 | 20,4 | 18 | 10,8 | 188,4 | 51,95 | 31,17 |
| 2 | 0 | 20,8 | 21,2 | 20,4 | 20,8 | 13,4 | 16,6 | 10,8 | 18 | 188,4 | 31,17 | 51,95 |
| 3 | 0 | 20,8 | 20,8 | 20,8 | 20,8 | 0 | 0 | 0 | 20,8 | 188,4 | 0 | 60,03 |
| 4 | 0 | 20,8 | 15 | 18,2 | 20,8 | 13,4 | 16,6 | 10,8 | 18 | 188,4 | 31,17 | 51,95 |
| 5 | 0 | 20,8 | 7,6 | 15,6 | 20,8 | 21,2 | 20,4 | 18 | 10,8 | 188,4 | 51,95 | 31,17 |
| 6 | 0 | 20,8 | 0 | 14 | 20,8 | 20,8 | 20,8 | 20,8 | 0 | 188,4 | 60,03 | 0 |
| 7 | 0 | 20,8 | 7,6 | 15,6 | 20,8 | 15 | 18,4 | 18 | 10,8 | 188,4 | 51,95 | 31,17 |
| 8 | 0 | 20,8 | 15 | 18,2 | 20,8 | 7,6 | 14,8 | 10,8 | 18 | 188,4 | 31,17 | 51,95 |
| 9 | 0 | 20,8 | 20,8 | 20,8 | 20,8 | 0 | 0 | 0 | 20,8 | 188,4 | 0 | 60,03 |
| 10 | 0 | 20,8 | 21,2 | 20,4 | 20,8 | 7,6 | 14,8 | 10,8 | 18 | 188,4 | 31,17 | 51,95 |
| 11 | 0 | 20,8 | 13,4 | 16,6 | 20,8 | 15 | 18,4 | 18 | 10,8 | 188,4 | 51,95 | 31,17 |
2.3 Побудова планів прискорень
Послідовність
побудови плану прискорень також визначається формулою будови механізму.
Спочатку визначимо прискорення провідної крапки A. При ![]() початкової ланки ОА крапка
А має тільки нормальне прискорення:
початкової ланки ОА крапка
А має тільки нормальне прискорення:
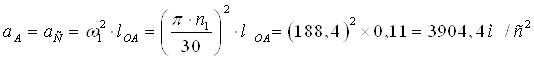
Прискорення
крапки А аА на плані прискорень зобразимо вектором ![]() , що спрямований по ланці
, що спрямований по ланці ![]() ОА від крапки А к крапці О. Масштабний
коефіцієнт плану прискорень
ОА від крапки А к крапці О. Масштабний
коефіцієнт плану прискорень ![]() вибираємо
стандартним.
вибираємо
стандартним.
![]()
Вектор
![]() і є план прискорень
початкової ланки ОА (кривошипа).
і є план прискорень
початкової ланки ОА (кривошипа).
А тепер побудуємо план прискорень групи 2, 3. Тут відомі прискорення крапок А и В. Запишемо два векторних рівняння, розглядаючи рух крапки B відносно А и стосовно крапки B0:
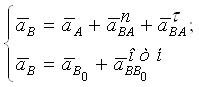
де ![]() - нормальне прискорення у
відносному русі крапки B стосовно крапки А;
- нормальне прискорення у
відносному русі крапки B стосовно крапки А;
![]() - тангенціальне прискорення
в тім же русі;
- тангенціальне прискорення
в тім же русі;
![]() - прискорення крапки B0
напрямної X–X;
- прискорення крапки B0
напрямної X–X;
![]() - прискорення крапки B
повзуну щодо крапки B0 приналежний.
- прискорення крапки B
повзуну щодо крапки B0 приналежний.
Вектор
нормального прискорення ![]() спрямований
паралельно АB від крапки B до крапки А. Величина цього прискорення
спрямований
паралельно АB від крапки B до крапки А. Величина цього прискорення
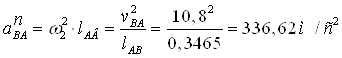
![]()
На
плані прискорень через крапку а проводимо пряму, паралельну ланці АB
відкладаємо на ній у напрямку від крапки B до крапки А вектор ![]() , що представляє в масштаб
, що представляє в масштаб
![]() прискорення
прискорення ![]()

Через
крапку n1 проводимо пряму в напрямку вектора тангенціального
прискорення ![]() перпендикулярно до ланки
АB.
перпендикулярно до ланки
АB.
У
відповідності із другим рівнянням через полюс p і співпадаючу з
ним крапку B0 (прискорення ![]() для
нерухливої напрямної) проводимо пряму в напрямку прискорення
для
нерухливої напрямної) проводимо пряму в напрямку прискорення ![]() паралельно напрямної X–X.
Крапка b перетинання цих прямих визначає кінець вектора абсолютного прискорення
крапки B.
паралельно напрямної X–X.
Крапка b перетинання цих прямих визначає кінець вектора абсолютного прискорення
крапки B.
![]()
Величина тангенціального прискорення
![]()
Прискорення центра мас S2 ланки АB визначається за допомогою теореми подоби. Із пропорції
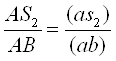
визначаємо положення крапки S2 на плані прискорень
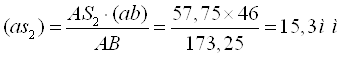
Отже, величина прискорення крапки S2
![]()
А зараз визначимо прискорення крапок ланок групи, утвореної ланками 4 і 5. Розглянемо рух крапки D щодо крапки C, а потім стосовно крапки D0.
Прискорення крапки D визначиться графічним рішенням наступних двох векторних рівнянь:
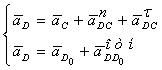
У
першому рівнянні нормальне прискорення ![]() спрямоване
по шатуні DC (від крапки D до крапки C). Величина прискорення
спрямоване
по шатуні DC (від крапки D до крапки C). Величина прискорення
![]()
Тангенціальне
прискорення ![]() перпендикулярно до ланки
DC, а величина його визначається побудовою плану прискорень.
перпендикулярно до ланки
DC, а величина його визначається побудовою плану прискорень.
Прискорення
![]() , а прискорення
, а прискорення ![]() крапки D повзуну щодо
крапки D0 напрямної визначиться побудовою плану прискорень.
крапки D повзуну щодо
крапки D0 напрямної визначиться побудовою плану прискорень.
Відповідно
до першого рівняння на плані прискорень через крапку b проводимо пряму,
паралельну ланці DC, і відкладаємо на ній у напрямку від крапки D до крапки C
вектор ![]() , що представляє в масштаб
, що представляє в масштаб
![]() прискорення
прискорення ![]()
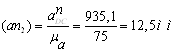
Через
крапку n2 проводимо пряму в напрямку вектора тангенціального
прискорення ![]() перпендикулярно до ланки
DC. Потім через полюс p і співпадаючу з ним крапку D0
проводимо пряму в напрямку прискорення
перпендикулярно до ланки
DC. Потім через полюс p і співпадаючу з ним крапку D0
проводимо пряму в напрямку прискорення ![]() паралельно
напрямної X–X. Крапка d перетинання цих прямих визначає кінець вектора повного
прискорення крапки D
паралельно
напрямної X–X. Крапка d перетинання цих прямих визначає кінець вектора повного
прискорення крапки D
![]()
Величина тангенціального прискорення
![]()
Прискорення центра мас S4 ланки CD визначається із пропорції
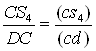
звідки
![]()
Отже, величина прискорення крапки S4
![]()
Визначимо величини кутових прискорень ланок:

Напрямок
кутового прискорення e4 шатуна 4
визначить вектор ![]() , перенесений у
крапку D на схемі механізму. Ланка буде обертатися по годинникової стрілки.
, перенесений у
крапку D на схемі механізму. Ланка буде обертатися по годинникової стрілки.
У такій же послідовності виробляється побудова плану прискорень для другого заданого положення механізму.
Таблиця 2.2
| № |
|
|
|
|
|
|
|
|
|
|
e2 |
e4 |
|
м/з2 |
с-2 |
|||||||||||
| 0 | 3904,4 | 5175 | 0 | 1248,6 | 3904,4 | 4837,5 | 4125 | 0 | 1350 | 2625 | 0 | 11904,76 |
| 2 | 3904,4 | 1350 | 3412,5 | 336,62 | 3904,4 | 2850 | 1875 | 935,1 | 3975 | 3825 | 9848,5 | 5411,3 |
2.4 Побудова кінематичних діаграм для крапки В
а). Діаграма переміщення
На осі абсцис відкладаємо відрізок l, що зображує час одного оберту кривошипа, ділимо його на 12 рівних частин і у відповідних крапках відкладаємо переміщення крапки У від початку відліку із плану положень механізму.
Масштаб по осі ординат µs= µl =0,002 м/мм
Масштаб
по осі абсцис 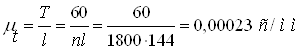
б). Діаграма швидкостей
Діаграма
швидкості крапки В побудована по даним планів швидкостей. Масштаб по ос
ординат ![]() прийнятий рівним масштабу
прийнятий рівним масштабу ![]() планів швидкостей
планів швидкостей 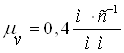 .
.
в). Діаграма прискорення
Діаграма прискорення побудована графічним диференціюванням (Методом хорд) діаграми швидкості.
Масштаб по осі ординат
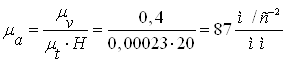
г). Точність побудови діаграми прискорення
Зрівняємо величини прискорення крапки В, отриманих за допомогою графічного диференціювання діаграми швидкостей і методом планів.
Для положення механізму 2 з діаграми прискорення маємо
![]()
а із плану прискорень
![]()
Розбіжність значень прискорень, отриманих двома методами
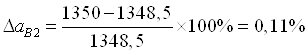
3. Кінетостатичне дослідження механізму двигуна. Дослідження руху механізму
3.1 Визначення сил і моментів сил, що діють на ланки механізму
Будуємо
кінематичну схему й план положень механізму в масштабі ![]() , план швидкостей у
масштабі
, план швидкостей у
масштабі ![]() , план прискорень у
масштабі
, план прискорень у
масштабі ![]() й індикаторній діаграм
компресора.
й індикаторній діаграм
компресора.
По ндикаторній діаграмі відповідно до розмітки ходу повзунів У и D визначаємо питомі тиски на поршень для кожного з положень механізму. Для цього будуємо ндикаторні діаграми для кожного повзуну, помістивши вісь S діаграм паралельно осі його руху. Проводячи з кожної крапки положення повзуну прямі, паралельн осі P, одержимо на діаграмі розмітку положень крапок D і В. При цьому необхідно врахувати, що порядок нумерацій положень на діаграмі повинен відповідати напрямку робочий і холостий ходи повзуну.
Масштаб ндикаторної діаграми по осі P:
![]()
де ![]() - заданий максимальний
питомий тиск на поршень, рівне 10 МПа;
- заданий максимальний
питомий тиск на поршень, рівне 10 МПа;
h прийнята висота індикаторної діаграми (50 мм).
Сила тиску газу на поршень
![]()
де P питомий тиск газу на поршень у Па (1Па= 1Н/м2);
d- діаметр поршня в м.
Для розрахункового положення (2) механізму:
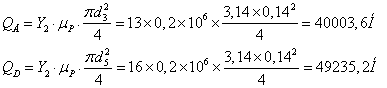
Сили ваги ланок прикладені до їхніх центрів ваги. Їхньої величини визначаємо по формулі:
![]() (Н),
(Н),
де m маса ланки в кг.
Сили ваги ланок 2 і 4:
![]()
Сили ваги ланок 3 і 5:
![]()
Сили нерції ланок визначаємо по формулі:
![]()
де as прискорення центра мас ланки в м/с2.
Напрямок
сили інерції ![]() протилежно напрямку
вектора (
протилежно напрямку
вектора (![]() ).
).
Сила нерції ланки 1 дорівнює нулю, тому що центр мас ланки лежить на осі обертання його прискорення дорівнює нулю.
Сила нерції ланки 2
![]()
Сила нерції ланки 3
![]()
Сила нерції ланки 4
![]()
Сила нерції ланки 5
![]()
Моменти сил інерций (інерційні моменти) ланок визначаємо по формулі:
![]()
Де IS – момент інерції маси ланки щодо осі, що проходить через центр мас перпендикулярно до площини руху (кгм2);
![]()
![]() - кутове прискорення
ланки (радий/з2).
- кутове прискорення
ланки (радий/з2).
Напрямок
моменту сил інерції ![]() протилежно
кутовому прискоренню ланки
протилежно
кутовому прискоренню ланки ![]() .
.
Момент
сил інерції ланки 1 дорівнює нулю, тому що його кутове прискорення дорівню
нулю (рівномірний обертовий рух при ![]() ).
).
Момент сил інерції ланки 2
![]()
Момент сил інерції ланки 4
![]()
Визначення реакцій у кінематичних парах починаємо із групи, що складається з ланок 4 і 5.
3.2 Силовий розрахунок групи Ассура, що складає з ланок 4 і 5
Групу
з ланок 4 і 5 вичерчуємо окремо в масштабі довжин ![]() у відповідних крапках прикладаємо сили ваги й сили інерції ланок, а до ланки 4
момент сил інерції
у відповідних крапках прикладаємо сили ваги й сили інерції ланок, а до ланки 4
момент сил інерції ![]() . Відкинут
зв'язки заміняються реакціями
. Відкинут
зв'язки заміняються реакціями ![]() й
й ![]() . Під дією зовнішніх сил,
сил інерції й реакцій група буде перебувати в рівновазі.
. Під дією зовнішніх сил,
сил інерції й реакцій група буде перебувати в рівновазі.
Становимо умову рівноваги групи, дорівнюючи нулю суму всіх сил, що діють на групу
![]() .
.
Невідомим
тут є реакція ![]() .
.
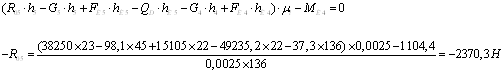
Для
визначення реакції ![]() будуємо план сил
у масштабі
будуємо план сил
у масштабі ![]() .
.
Із
крапки a паралельно силі ![]() відкладається
відрізок
відкладається
відрізок
![]()
з
кінця вектора аb у напрямку сили ![]() відкладаємо
відрізок bc
відкладаємо
відрізок bc
![]()
з
кінця вектора bc у напрямку сили ![]() відкладаємо
вектор cd
відкладаємо
вектор cd
![]()
з
кінця вектора сd у напрямку сили інерції![]() відкладаємо
вектор de
відкладаємо
вектор de
![]()
з
кінця вектора de у напрямку сили ![]() відкладаємо
відрізок ef
відкладаємо
відрізок ef
![]()
з
кінця вектора ef у напрямку сили ![]() відкладаємо
відрізок fg
відкладаємо
відрізок fg
![]()
З'єднавши
крапку g із крапкою а на плані сил, одержимо вектор ![]() ,
що зображує собою шукану реакцію
,
що зображує собою шукану реакцію ![]() ,
величина якої
,
величина якої
![]() .
.
Реакція
в шарнірі D ![]() визначається вектором cg
плану сил. Величина реакції
визначається вектором cg
плану сил. Величина реакції
![]() .
.
3.3 Силовий розрахунок групи Ассура, що складає з ланок 2 і 3
Групу
з ланок 2 і 3 вичерчуємо окремо в масштабі довжин ![]() =0,0025 м/мм
у відповідних крапках прикладаємо сили ваги й сили інерції ланок. Умова
рівноваги групи виразиться наступним векторним рівнянням:
=0,0025 м/мм
у відповідних крапках прикладаємо сили ваги й сили інерції ланок. Умова
рівноваги групи виразиться наступним векторним рівнянням:
![]()
У
даному рівнянні невідомі дві реакції ![]() й
й ![]() . Напрямок реакції
. Напрямок реакції ![]() відомо: вона
перпендикулярна до напрямного поршня 3.
відомо: вона
перпендикулярна до напрямного поршня 3.
Величину
реакції ![]() визначимо з рівняння
моментів всіх сил, прикладених до ланок 2 і 3, щодо крапки А: R03=6890,5
Н.
визначимо з рівняння
моментів всіх сил, прикладених до ланок 2 і 3, щодо крапки А: R03=6890,5
Н.
Для
визначення реакції ![]() будуємо план сил
у масштабі
будуємо план сил
у масштабі ![]() . З'єднавши крапку g із
крапкою а на плані сил, одержимо вектор gа, що зображує собою шукану реакцію
. З'єднавши крапку g із
крапкою а на плані сил, одержимо вектор gа, що зображує собою шукану реакцію ![]() , величина якої
, величина якої
![]()
Реакція
в шарнірі B ![]() визначається вектором
визначається вектором ![]() плану сил. Величина
реакції
плану сил. Величина
реакції
![]()
3.4 Силовий розрахунок початкової ланки
Вичерчуємо
окремо початкова ланка в масштабі ![]() й у
прикладаємо діючі сили: у крапці А реакцію
й у
прикладаємо діючі сили: у крапці А реакцію ![]() ,
силу, що
,
силу, що ![]() врівноважує,
перпендикулярно до ланки ОА.
врівноважує,
перпендикулярно до ланки ОА.
Векторне рівняння рівноваги початкової ланки має вигляд:
![]() .
.
Величину сили, що врівноважує, визначаємо з рівняння моментів всіх сил щодо крапки О.
![]()
![]()
У
масштабі ![]() будуємо план сил
початкової ланки, з якого визначаємо реакцію
будуємо план сил
початкової ланки, з якого визначаємо реакцію ![]() в
шарнірі О. Величина реакції:
в
шарнірі О. Величина реакції:
![]()
3.5 Визначення сили, що врівноважує, по методу Н. Жуковського
Більше простим методом визначення сили, що врівноважує, є метод Н.Е. Жуковського.
У довільному масштабі будуємо план швидкостей, повернений на 90 ((у нашім випадку за годинниковою стрілкою), і у відповідних крапках його прикладаємо сили тиску газу на поршні, сили ваги ланок, сили інерції ланок і моменти сил інерції, що врівноважує силу.
Момент
сил інерції ![]() представляємо у вигляд
пари сил
представляємо у вигляд
пари сил ![]() і
і ![]() , прикладених у крапках A
В, із плечем пари
, прикладених у крапках A
В, із плечем пари ![]() . Величина цих
сил:
. Величина цих
сил:
![]()
Момент
сил інерції ![]() представляємо у вигляд
пари сил
представляємо у вигляд
пари сил ![]() і
і ![]() , прикладених у крапках С и
D, із плечем пари
, прикладених у крапках С и
D, із плечем пари ![]() . Величина цих
сил:
. Величина цих
сил:
![]()
Повернений план швидкостей із прикладеними силами, розглянутий як твердий важіль із опорою в полюсі, буде перебувати в рівновазі.
Становимо рівняння моментів всіх сил щодо полюса плану швидкостей, взявши плечі сил по кресленню в мм:

Величина
сили, що врівноважує, отриманої при кінетостатичному розрахунку ![]() .
.
Розбіжність
результатів визначення сили, що врівноважує, методом планів сил і методом
Жуковського ![]() .
.
3.6 Визначення миттєвого механічного коефіцієнта корисної дії механізму
Миттєвий механічний коефіцієнт корисної дії механізму визначимо для розрахункового положення 2.
Уважаємо,
що радіуси цапф шарнірів задані r = 20 мм, коефіцієнти тертя в шарнірах
напрямних повзунів також задані й рівні відповідно ![]() .
.
Припустимо, що всі виробничі опори в механізмі зводяться до опору тертя. Реакції в кінематичних парах для даного положення механізму визначені силовим розрахунком рівні
![]()
![]()
Для визначення потужностей, що витрачаються на тертя в різних кінематичних парах, необхідно знайти відносні кутові швидкості в шарнірах і відносні швидкості в поступальних парах.
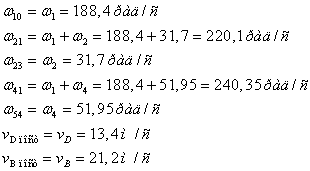
Потужності, затрачувані на тертя в кінематичних парах у цей момент часу, рівні:

Загальна потужність сил тертя:
![]()
Потужність рушійних сил у цей момент часу
![]() Bт
Bт
![]()
3.7 Дослідження руху механізму й визначення моменту інерції маховика
Тому що усередині циклу усталеного руху машини не спостерігається рівності роботи рушійних сил і роботи сил опору й сталості наведеного моменту інерц механізму, те кутова швидкість (провідної ланки виявляється змінною. Величина коливань цієї швидкості оцінюється коефіцієнтом нерівномірності ходу
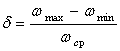
де wmax – максимальна кутова швидкість;
wmin – мінімальна кутова швидкість;
wср. – середня кутова швидкість.
За
середню кутову швидкість можна прийняти номінальну швидкість ![]() .
.
Коливання швидкості провідної ланки механізму повинна регулюватися в заздалегідь заданих межах. Це регулювання звичайно виконується відповідним підбором мас ланок механізму. Маси ланок механізму повинні підбиратися так, щоб вони могли накопичувати (акумулювати) всі збільшення кінетичної енергії при перевищенн роботи рушійних сил над роботою сил опору.
Роль
акумулятора кінетичної енергії механізму звичайно виконує маховик. Тому в наше
завдання входить підібрати масу маховика такий, щоб даний механізм міг
здійснити роботу із заданим коефіцієнтом нерівномірності руху ![]() .
.
Для розрахунку маховика скористаємося методом енергомас. По цьому методі момент нерції маховика визначається по діаграмі енергомас, що характеризує залежність збільшення кінетичної енергії механізму від наведеного моменту інерц механізму.
Тому що збільшення кінетичної енергії дорівнює різниці роботи рушійних сил і роботи сил опору, то для побудови цієї діаграми необхідно побудувати спочатку діаграми наведених моментів рушійних сил і сил опору.
Наведений до провідної ланки момент сил для кожного положення досліджуваного механізму.
![]()
Для розрахункового 2-го положення:
![]()
Розрахунок наведеного моменту рушійних сил для інших положень механізму зводимо в таблицю 3.1
Таблиця 3.1-результати розрахунку наведеного моменту рушійних сил
| № |
|
|
|
|
|
| 0 | 153860 | 0 | -4615,8 | 20,8 | -509,6 |
| 1 | 107702 | 13,4 | -15386 | 21,2 | 5929 |
| 2 | 40003,6 | 21,2 | -49235,2 | 13,4 | 999,6 |
| 3 | 15386 | 20,8 | 153860 | 0 | 1698,7 |
| 4 | 10770,2 | 15 | 104624,8 | 13,4 | 8299 |
| 5 | 9231,6 | 7,6 | 55389,6 | 21,2 | 6605,2 |
| 6 | 7693 | 0 | 18463,2 | 20,8 | 2038,4 |
| 7 | 0 | 7,6 | 12308,8 | 15 | 980 |
| 8 | 0 | 15 | 9231,6 | 7,6 | 372,4 |
| 9 | -3077,2 | 20,8 | 7693 | 0 | -339,7 |
| 10 | -13847,4 | 21,2 | 0 | 7,6 | -1558,2 |
| 11 | -49235,2 | 13,4 | 0 | 15 | -3501,9 |
На
підставі дані таблиці будуємо діаграму зміни Мд рушійних сил у
функції кута повороту початкової ланки. Масштаб по осі ординат вибираємо ![]() , масштаб по осі абсцис при
довжині діаграми l=180 мм
, масштаб по осі абсцис при
довжині діаграми l=180 мм
![]()
Тому що робота рушійних сил
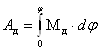 ,
,
те графічним інтегруванням діаграми наведених моментів рушійних сил будуємо діаграму робіт рушійних сил. Масштаб по осі ординат визначається по формулі
![]()
де Н полюсна відстань, рівне 50 мм.
За один цикл усталеного руху (у нашім випадку один оберт провідної ланки) робота рушійних сил дорівнює роботі сил опору.
Приймемо
постійним наведений момент сил опору(![]() ) Тод
робота сил опору
) Тод
робота сил опору 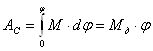 , являє собою
лінійну функцію кута повороту провідної ланки. З'єднавши початок координат з
останньою крапкою діаграми роботи сил опору, одержимо похилу пряму, що
представляє собою діаграму роботи рушійних сил.
, являє собою
лінійну функцію кута повороту провідної ланки. З'єднавши початок координат з
останньою крапкою діаграми роботи сил опору, одержимо похилу пряму, що
представляє собою діаграму роботи рушійних сил.
Продиференцирував графічно отриману пряму, на діаграмі рушійних моментів сил одержимо горизонтальну пряму визначальну величину постійного наведеного моменту рушійних сил.
Тому що збільшення кінетичної енергії
![]()
те для побудови діаграми збільшення кінетичної енергії або надлишкової роботи необхідно з ординат діаграми роботи рушійних сил відняти ординати діаграми робіт сил опору.
Масштаби по координатних осях залишаються ті ж, що й для діаграми робіт.
3.8 Визначення наведених моментів інерції механізму
Для ланки, що робить поступальний рух (повзун), кінетична енергія
![]() ,
,
де m маса ланки;
v- швидкість поступального руху
Для ланки, що робить обертовий рух (кривошип, коромисло), кінетична енергія
![]()
де J момент інерції щодо осі обертання;
(– кутова швидкість ланки.
Кінетична енергія ланки, що робить складний плоскопаралельний рух
![]() ,
,
де vS – швидкість центра мас ланки;
JS -момент інерції ланки щодо осі, що проходить через центр мас.
Складывая кінетичні енергії всіх ланок, одержимо повну кінетичну енергію механізму.
У нашім прикладі повна кінетична енергія механізму

Вираження у квадратних дужках являє собою наведений до початкової ланки момент інерц механізму.
Обчислимо наведений момент інерції для 12-ти положень механізму.
Для 2-го положення механізму
![]()
![]()
Обчислення наведеного моменту інерції для інших положень механізму зводимо в таблицю 3.2.
За
даними таблиці будуємо діаграму наведеного моменту інерції механізму у функц
кута повороту початкової ланки. Приймаємо масштаб ![]()
Методом
виключення загального параметра j з діаграм ![]() і
і ![]() будуємо діаграму енергомас
будуємо діаграму енергомас
![]()
Таблиця 3.2-результати розрахунку наведеного моменту інерції механізму
| № |
|
|
|
|
|
|
|
|
| 0 | 0,15 | 0,0207 | 0,0552 | 0 | 0 | 0,1219 | 0,0463 | 0,3941 |
| 1 | 0,15 | 0,0155 | 0,0776 | 0,0192 | 0,0056 | 0,1172 | 0,0481 | 0,4332 |
| 2 | 0,15 | 0,0056 | 0,1172 | 0,0481 | 0,0155 | 0,0776 | 0,0192 | 0,4332 |
| 3 | 0,15 | 0 | 0,1219 | 0,0463 | 0,0207 | 0 | 0 | 0,3389 |
| 4 | 0,15 | 0,0056 | 0,0933 | 0,0241 | 0,0155 | 0,0776 | 0,0192 | 0,3889 |
| 5 | 0,15 | 0,0155 | 0,0686 | 0,0062 | 0,0056 | 0,1172 | 0,0481 | 0,3853 |
| 6 | 0,15 | 0,0207 | 0,0552 | 0 | 0 | 0,1219 | 0,0463 | 0,4112 |
| 7 | 0,15 | 0,0155 | 0,0686 | 0,0062 | 0,0056 | 0,0954 | 0,0241 | 0,3941 |
| 8 | 0,15 | 0,0056 | 0,0933 | 0,0241 | 0,0155 | 0,0617 | 0,0062 | 0,3654 |
| 9 | 0,15 | 0 | 0,1219 | 0,0463 | 0,0207 | 0 | 0 | 0,3389 |
| 10 | 0,15 | 0,0056 | 0,1172 | 0,0481 | 0,0155 | 0,0617 | 0,0062 | 0,4043 |
| 11 | 0,15 | 0,0155 | 0,0776 | 0,0192 | 0,0056 | 0,0954 | 0,0241 | 0,3874 |
По
даному коефіцієнті нерівномірності руху d=1/95 і середньої кутово
швидкості ![]() визначаємо кути ymax. і ymin, утворен
дотичними до діаграми енергомас із віссю абсцис,
визначаємо кути ymax. і ymin, утворен
дотичними до діаграми енергомас із віссю абсцис,
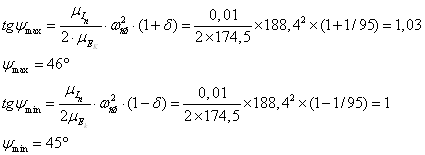
Побудувавши сторони цих кутів і перенесучи їх паралельно самим собі до моменту торкання із кривій енергомас відповідно зверху й знизу, одержимо на осі DEДо відрізок mn, ув'язнений між цими дотичними.
По відрізку mn визначаємо момент інерції маховика
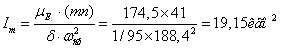
Діаметр маховика, виконаного у вигляді суцільного диска, визначається по формулі:
![]() ,
,
де ![]() - питома вага матеріалу
маховика (чавун);
- питома вага матеріалу
маховика (чавун);
(=0,1. Тоді
![]()
Маховий
момент ![]()
![]() кгм2
кгм2
Тод маса маховика
![]()
а ширина обода
![]()
4. Проектування кулачкового механізму
Широке застосування кулачкових механізмів обумовлене тим, що з їхньою допомогою легко відтворюється заданий закон руху веденої ланки.
Потрібно мати на увазі, що при виборі закону руху веденої ланки можуть виникнути удари в кулачковому механізмі. Розрізняють наступні групи законів руху: із твердими ударами, з м'якими ударами, без ударів. Тверді удари в кулачковому механізм мають місце, коли підйом або опускання штовхача відбувається з постійною швидкістю. При синусоїдальному законі рух відбувається без твердих і м'яких ударів (цей закон рекомендується при проектуванні швидкохідних кулачкових механізмів).
Для синтезу (проектування) кулачкового механізму задаються: схема механізму; максимальне лінійне h або кутове y переміщення ведено ланки; фазові кути повороту кулачка (видалення – jв, далекого стояння jбуд.с., повернення jв); закони руху вихідної ланки для фази видалення й повернення; довжина коромисла l для коромисловых кулачкових механізмів. Виходячи з умов обмеження кута тиску, визначають основн розміри ланок кулачкового механізму; мінімальний радіус кулачка, положення коромисла щодо центра обертання кулачка, проектують профіль кулачка графічним або аналітичним методами.
4.1 Побудова діаграм руху штовхача
Вичерчуємо
діаграму аналога прискорення коромисла 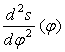 ,
для чого на осі абсцис у довільному масштабі mj відкладаємо
задані кути jв=95°, jбуд.с.= 20°, jв=160°. Для прийнято
довжини діаграми X=230 мм величини відрізків, що зображують фазові кути:
,
для чого на осі абсцис у довільному масштабі mj відкладаємо
задані кути jв=95°, jбуд.с.= 20°, jв=160°. Для прийнято
довжини діаграми X=230 мм величини відрізків, що зображують фазові кути:
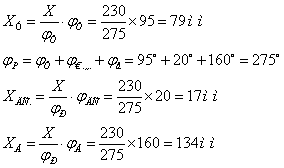
Для побудови графіка переміщення вихідної ланки по куті повороту кулачка необхідно виконати дворазове інтегрування другої похідної від переміщення вихідної ланки по куті повороту кулачка.
В нтервалі кута видалення jв у довільному масштабі будуємо закон рівномірно убутного прискорення, також і а в інтервал кута повернення jв.
Для
побудови діаграми аналога швидкості ![]() ,
нтегруємо побудовану діаграму
,
нтегруємо побудовану діаграму 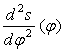 , для
чого відрізки Xу й Xв ділимо на 6 рівних частин.
, для
чого відрізки Xу й Xв ділимо на 6 рівних частин.
Через крапки 1,2,3…, 13 проводимо ординати, які ділять всю площу заданих діаграм на ряд ділянок. Площа кожного з ділянок заміняємо рівновеликим прямокутником із загальною підставою на осі абсцис. Проектуємо висоти отриманих трикутників на вісь ординат. Крапки проекцій 1', 2', 3',…, 13' з'єднуємо з полюсом P2, узятим на довільній полюсній відстані H2 від початку O осей координат променями P21', P22', P23',…, P213'.
Вісь
абсцис діаграми ![]() , ділимо на таку
ж кількість рівних частин, як і вісь абсцис діаграми
, ділимо на таку
ж кількість рівних частин, як і вісь абсцис діаграми 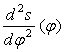 . Із крапки Про паралельно
промінь P21' проводимо лінію до перетинання її в крапці 1'' з
ординатою 1. Із крапки 1'' паралельно лучу P22' проводимо пряму до
перетинання з ординатою 2 і т.д. Отримана ламана і являє собою приблизно шукану
нтегральну криву
. Із крапки Про паралельно
промінь P21' проводимо лінію до перетинання її в крапці 1'' з
ординатою 1. Із крапки 1'' паралельно лучу P22' проводимо пряму до
перетинання з ординатою 2 і т.д. Отримана ламана і являє собою приблизно шукану
нтегральну криву ![]() на ділянці, що
відповідає куті jу повороту кулачка.
на ділянці, що
відповідає куті jу повороту кулачка.
Діаграма цієї функції на ділянці, що відповідає куті jУ будується аналогічним способом.
Діаграму
переміщень коромисла S(j) також будуємо методом графічного
нтегрування кривій ![]() .
.
Обчислимо масштаби діаграм. Масштаб по осі абсцис діаграм
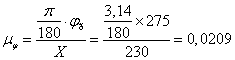 радий/мм
радий/мм
Масштаб по осі ординат діаграми переміщень
![]()
де h =30 мм – максимальне переміщення штовхача (центра ролика);
Sмах – максимальна ордината діаграми переміщень.
В нтервалі кута видалення
![]()
в нтервалі кута повернення
![]()
Масштаб
по осі ординат діаграми ![]()
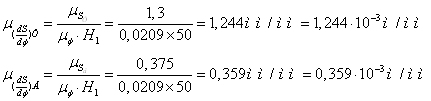
Масштаб
по осі ординат діаграми 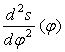
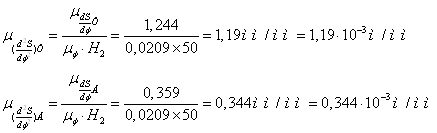
Розмітку траєкторії крапки В (центра ролика) робимо відповідно до діаграми S(j), для чого ліворуч від осі ординат під довільним кутом проводимо пряму й на ній відкладаємо відрізок O, дорівнює максимальному переміщенню штовхача в масштаб 2:1. Кінцеву крапку B6 з'єднуємо з кінцевою крапкою 6' проекц найбільшої ординати 6–6. Через крапки 1', 2',…, 5' проводимо прямі, паралельн 6' – B6. Отримані крапки B1, B2,…, B6 дають розмітку траєкторії коромисла в інтервалі кута видалення.
Аналогічно здійснюємо розмітку траєкторії крапки В коромисла в інтервалі кута повернення.
4.2 Побудова профілю кулачка коромислового кулачкового механізму
4.2.1 Визначення мінімального радіуса кулачка rmin і міжосьово відстані в коромисловом кулачковому механізмі
З
довільної крапки А проводимо дугу радіусом рівним довжині коромисла ![]() =100 мм, на якій
відзначаємо крапку В0 – початкове положення центра ролика коромисла.
=100 мм, на якій
відзначаємо крапку В0 – початкове положення центра ролика коромисла.
Від крапки В0 відкладаємо хід центра ролика В0У6=30 мм переносимо на нього розмітку траєкторії при видаленні й поверненні.
По діаграмі визначаємо максимальні значення аналогів швидкостей при видаленні й поверненні коромисла
Визначимо
значення ![]() для 3-го й 10-го положень:
для 3-го й 10-го положень:
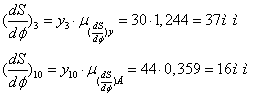
Для нших положень розрахунки проводимо аналогічно, і результати зводимо в таблицю 4.1.
Таблиця 4.1 – Результати розрахунку аналогів швидкостей
| Показник | № положення | ||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|
|
0 | 9 | 28 | 37 | 28 | 9 | 0 | 0 | 8,8 | 14 | 16 | 14 | 8,8 |
Відкладаємо
ці значення на паралельних прямих у масштабі ![]()
Із
крапки B3 відкладаємо відрізок ![]() у напрямку обертання
кулачка, а в протилежну сторону відрізок
у напрямку обертання
кулачка, а в протилежну сторону відрізок ![]() . Аналогічно визначаємо
нші відрізки для інших положень і будуємо діаграму
. Аналогічно визначаємо
нші відрізки для інших положень і будуємо діаграму ![]() ,
до якої проводимо дотичні під кутами
,
до якої проводимо дотичні під кутами ![]() .Крапка перетинання
цих дотичних визначить положення центра обертання кулачка – крапку ПРО (а
заштрихована площа є областю можливого розташування кулачка).
.Крапка перетинання
цих дотичних визначить положення центра обертання кулачка – крапку ПРО (а
заштрихована площа є областю можливого розташування кулачка).
Мінімальний радіус кулачка:
rmin=OB0×mS =21 × 0,001 =0,021 м
Побудова профілю кулачка коромислового кулачкового механізму.
Головним етапом синтезу кулачкового механізму є побудова профілю кулачка, в основу якого покладений метод зверненого руху. Суть цього методу полягає в тім, що всім ланкам механізму умовно повідомляється додаткове обертання з кутовою швидкістю, рівної кутової швидкості кулачка, спрямованої у зворотну сторону. Тоді кулачок зупиниться, а стійка разом з коромислом прийде в обертовий рух навколо центра кулачка О с кутовою швидкістю – wк. Крім того, штовхач буде робити ще рух відносно стійкі за законом, що визначається профілем кулачка.
Із центра Про проводимо окружності радіусами rmin і lАВ. Визначаємо положення центра ролика коромисла, для чого із крапки А радіусом, рівним довжині коромисла, проводимо дугу до перетинання з окружністю радіуса rmin. Крапка перетинання В0 і є положення центра ролика коромисла, що відповідає початку видалення. На траєкторію крапки В коромисла наносимо розмітку її відповідно до діаграми S(j). Одержуємо крапки В1, В2, В3…В6.
Для визначення дійсного профілю кулачка необхідно визначити радіус ролика. Радіус ролика повинен бути менше максимального радіуса кривизни rmin центрового (теоретичного) профілю кулачка:
![]() (0,7¸0,8) rmin
(0,7¸0,8) rmin
З конструктивних міркувань радіус ролика не рекомендується приймати більше половини мінімального радіуса:
rp £ (0,4 ¸0,5) rmin
![]() м
м
Приймаємо rp рівним 9 мм.
Дійсний (практичний) профіль кулачка одержимо, якщо побудуємо еквидистантну криву радіусом, рівним rp.
5. Проектування евоволентного зачеплення прямозубих циліндричних коліс
Приймаємо, що зубчасті колеса виготовлені без зсуву вихідного контуру (X1=X2=0). Тоді кут зачеплення дорівнює куту профілю інструмента (aw =a=20°), ділильн окружності є одночасно початковими окружностями зачеплення (rw1 = r1 rw2 = r2). Зубчаста передача, що розраховується, ма наступні параметри:
Z1 = 20; Z2 = 15; m = 9 мм
Радіуси початкових окружностей коліс
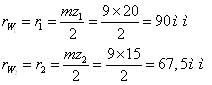
Радіуси основних окружностей коліс
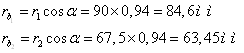 ;
;
Радіуси окружностей вершин зубів
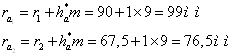 ;
;
де ![]() =1 – коефіцієнт висоти
головки зуба, а
=1 – коефіцієнт висоти
головки зуба, а ![]() – висота головки
зуба (відстань, обмірювана по радіусі між ділильною окружністю й окружністю
вершин).
– висота головки
зуба (відстань, обмірювана по радіусі між ділильною окружністю й окружністю
вершин).
Радіуси окружностей западин коліс
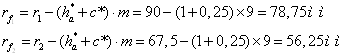
де з*=0,25 коефіцієнт радіального зазору;
с=c*m радіальний зазор, мм.
Крок по ділильній окружності
![]() мм
мм
Окружна товщина зуба по ділильній окружності
![]() мм
мм
Міжосьова відстань
aw = a = rw1+rw2 = 90+67,5=157,5 мм
де a=r1+r2 – ділильна міжосьова відстань, мм.
Висота зуба визначається як
h=ha+hf=h*a×m+(h*а+з*)× m =1![]() 9+(1+0,25)
9+(1+0,25)![]() 9=20,25 мм,
9=20,25 мм,
h= 2,25m =2,25 × 9 = 20,25 мм.
Для побудови профілів зачеплення зубчастих коліс вибираємо масштаб 2:1, значить на кресленні всі отримані значення величин збільшитися в 2 рази.
Побудова профілів зубів проводимо в наступному порядку:
- відкладаємо міжосьова відстань aw (O1O2 на кресленні);
- Радіусами rw1 і rw2 проводимо початков окружності коліс. Крапка P торкання їх є полюсом зачеплення;
- проводимо основні окружності коліс, окружності вершин зубів окружності западин;
- через полюс зачеплення P проводимо загальну дотичну t-t до початкових окружностей коліс і лінію зачеплення n-n, що стосується в крапках A B основних окружностей. Частина ab лінії n-n, укладена між окружностями вершин зубів, називається активною лінією зачеплення, тобто геометричним місцем дійсного торкання профілів зубів;
- будуємо евоволенти профілів зубів, що стикаються в полюс зачеплення P. Профілі зубів одержують обкатуючи лінію зачеплення як по однієї, так і по основним окружностям. При обкатуванні крапка P лінії зачеплення опису евоволенти f1e1 і f2e2, як шуканими профілями. Для побудови евоволентного профілю зуба першого колеса відрізок AP ділимо на рівні частини (у нашім випадку на 4). На основній окружності першого колеса вправо й уліво від крапки A відкладаємо дуги, довжини яких дорівнюють цим відрізкам, одержуємо крапки 1', 2', 3', 4', 5', 6' і 7'. Через ці крапки проводимо дотичні до основної окружності радіуса rb1 (перпендикуляри до відповідних радіусів). На дотичній, проведеної через цю крапку 1', відкладемо 1/4 відрізка AP. На дотичній, проведеної через крапку 2 відкладемо 2/4 відрізка AP і т.д. Провівши аналогічні побудови на кожній з дотичних, одержимо ряд крапок 1'', 2'', 3'',…, 7''. Плавна крива, проведена через отримані крапки, є евольвентним профілем правої частини зуба першого колеса. Таким же способом будується евольвентний профіль зуба другого колеса (для цього використовується відрізок (BP));
профіль
ніжки зуба, що лежить усередині основної окружності, окреслюється по радіальній
прямій, що з'єднує початок евоволенти з початком колеса, і сполучається з
окружністю западин закругленням радіуса ρ=0,4m=0,4×9=3,6 мм по
початковій окружності відкладаємо половину товщини зуба ![]() , проводимо вісь симетр
зуба (радіальну пряму) і за законами симетрії будуємо лівий профіль зуба;
, проводимо вісь симетр
зуба (радіальну пряму) і за законами симетрії будуємо лівий профіль зуба;
- на кожному колесі праворуч і ліворуч від побудованого по крапках зуба будуємо ще два зуби (за допомогою шаблонів або лекал).
При обертанні першого колеса (допустимо в напрямку обертання годинникової стрілки) ніжка його зуба ввійде в зачеплення в крапці a з головкою зуба другого колеса. У крапці b головка зуба першого колеса вийде із зачеплення з ніжкою зуба другого колеса. Таким чином, крапка зачеплення (зіткнення зубів) переміщається по профілі зуба першого колеса від його підстави до вершини, а по профілі зуба другого – навпаки, від вершини до підстави.
Ділянки профілів зубів, які в процесі передачі обертання входять у зіткнення один з одним, називають активними профілями. Визначимо ці ділянки. Крапку f1 на профілі зуба першого колеса одержимо, якщо із центра O1 описати дугу O1a радіусом O1a. Точно також знаходимо крапку f2, описавши дугу O2b із центру O2.
У крапці a зустрінуться крапки f1 і e2, а в крапці b вийдуть із зачеплення крапки e1 і f2. Активними профілями частини евольвент e1f1 і e2f2.
Щоб побудувати дугу зачеплення на першому зубчастому колесі, профіль цього колеса повернемо навколо крапки O1 і сполучимо послідовно з початком кінцем активної лінії зачеплення, тобто із крапками a і b. На початковій окружності першого колеса одержимо дугу c'd'. Якщо повернемо профіль зуба другого колеса навколо крапки O2 і сполучимо із крапками a і b, то на початковій окружності другого колеса одержимо дугу c «d». Дуги c'd' і c «d» дугами зачеплення по початкових окружностях, дуги ab' і a'b – дугами зачеплення по основних окружностях.
Довжина
дуги зачеплення по основній окружності колеса дорівнює довжині ![]() активної лінії зачеплення
ab.
активної лінії зачеплення
ab.
Кути ja1 і ja2 називаються
кутами перекриття. Відношення кута перекриття зубчастого колеса до його
кутового кроку t =![]() називається
коефіцієнтом перекриття
називається
коефіцієнтом перекриття
![]()
![]() .
.
Обчислимо коефіцієнт перекриття проектованої передачі. Із креслення довжина активно лінії зачеплення дорівнює 82 мм, що відповідає дійсному значенню ga = (ab) = 41 мм. Тоді коефіцієнт перекриття
![]()
Коефіцієнт перекриття можна обчислити також аналітично по формулі
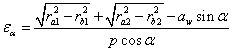
![]()
Коефіцієнт перекриття показує середнє число пар зубів, що одночасно перебувають у зачепленні. Якщо ea = 1,52, то 52% часу в зачепленні беруть участь дві пари зубів, а 48% часу – одна пара.
Питоме ковзання профілів зубів (n1 і n2) характеристикою ковзання одного профілю зуба по другому, тобто характеризу зношування профілів, викликаний появою сил тертя.
Питоме ковзання можна визначити по формулах
![]() ;
;
![]() ;
;
де r1 - радіус кривизни евоволенти першого колеса в крапці зачеплення;
r2 – радіус кривизни евоволенти другого колеса в крапці зачеплення;
u12, u21 – передатне відношення щабля.
Передатне відношення для зовнішнього зачеплення визначається як
![]() ;
; ![]() .
.
Обчислимо питоме ковзання в декількох крапках зачеплення й побудуємо діаграми питомого ковзання. Вісь абсцис діаграм проведемо паралельно лінії зачеплення, а вісь ординат перпендикулярно до неї через крапку A. Спроектуємо на вісь абсцис крапки A, a, P, b і B. Тоді r1 = x, r2 = g2-x (g2 – довжина лінії зачеплення AB).
У нашім випадку аb = 82 мм у масштабі 2:1.
![]() ;
;
Значення поточної координати X візьмемо з інтервалом в 15 мм у межах від X =0 до X =108 мм. Результати обчислень n1 і n2 наведені в таблиці
Таблиця 5.1 – Результати розрахунку питомих ковзань профілів зубів
|
x=r1 |
0 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 108 |
|
ga-x=r2 |
108 | 93 | 78 | 63 | 48 | 33 | 18 | 3 | 0 |
|
n1 |
- |
-7,26 | -2,47 | -0,87 | -0,07 | 0,41 | 0,73 | 0,96 | 1 |
|
n2 |
1 | 0,88 | 0,71 | 0,46 | 0,06 | -0,7 | -3,75 | -25,25 |
- |
Тому що зачеплення профілів зубів коліс відбувається тільки на активній лін зачеплення, то для більшої наочності ці ділянки заштриховані.
Товщину
зуба першого колеса по окружності вершин визначимо по формулі 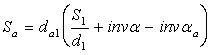 , де aa – кут профілю евоволенти
на окружності вершин зубів;
, де aa – кут профілю евоволенти
на окружності вершин зубів;
![]()
inv 20°=0,014904; inv 31,24°=0,061400
![]()
Для нормально роботи зубчастої передачі необхідно, щоб дотримувалися наступні умови:
1) ea ³ 1,1;
2) Sa ³ 0,3m (відсутність загострення головки зуба в меншого колеса).
У
нашім випадку![]() й
й ![]() , обоє умови задовольняються.
, обоє умови задовольняються.
Таким чином, при рішенні питання щодо вибору й виготовлення зубчастої передачі в кожному окремому випадку необхідно виходити з аналізу експлуатаційних властивостей передачі – тривалості зачеплення й питомого ковзання евоволентних профілів зубів.
6. Проектування зубчастого механізму
6.1 Аналітичний метод
Передатному відношенню привласнюється знак мінус при зовнішнім зачепленні, знак плюс – при внутрішньому. Знак передатного відношення вказує напрямок обертання ведено ланки стосовно ведучого.
Планетарним називається механізм, у якому геометричні осі деяких зубчастих коліс рухливими. Простий планетарний механізм володіє одним ступенем волі (W=1).
Існу кілька методів визначення передатних відносин планетарних механізмів.
Аналітичний метод.
U1H=U12×U23×U3H,
де ![]() ;
;
U3H
=1– (![]() )×
)×![]() )=3,24
)=3,24
По рівнянню співвісності:
rw3´ + rw4 = rw5 – rw4
![]()
![]()
![]()
Z5=![]()
![]()
Шляхом підбора визначаємо числа зубів
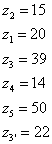
![]()
Передатне відношення спроектованого механізму відрізняється від заданого на невелику величину.
![]()
![]()
6.2 Графічний метод
Для планетарних механізмів із циліндричними колесами план лінійних швидкостей будується в такий спосіб.
Вкреслиться кінематична схема механізму в масштабі довжин, обумовлених по формулі
![]() ,
,
де d довжина відрізка, що зображує на кресленні ділильний діаметр колеса l, мм.
![]()
Тому що крапки 1 і H перебувають по різних сторонах від осі y-y, те передатне відношення негативне.
Погрішність розрахунку
![]()
Висновок
У процесі виконання курсового проекту отримані навички дослідження й проектування механізмів і машин, користування довідковою літературою.
Зроблений структурний і кінематичний аналіз механізму.
Визначен реакції в кінематичних парах, величини сили, що врівноважує, миттєвого коефіцієнта корисної дії механізму, зроблений розрахунок махових мас механізму по заданому коефіцієнті нерівномірності руху.
Були виконані наступні завдання:
– розрахунок геометричних розмірів зубчастої передачі;
– визначення коефіцієнта перекриття питомих ковзань;
– оцінка проектованої передачі за геометричними показниками;
– визначення основних розмірів і геометрії профілю кулачка, забезпечення відтворення необхідного закону руху штовхача.
Література
1. Збірник завдань по теор механізмів і машин // Артоболевський І.І., Едельштейн Б.В. – К., 1972.
2. Завдання й вправи по теорії механізмів і машин / під ред. Н.В. Алехновича. – К., 1990.
3. Курсове проектування по теор механізмів і машин / під ред. Г.Н. Девойко. – К., 1986.
4. Озол, О.Г. Теорія механізмів і машин / О.Г. Озол. – К., 1984.
5. Попов, С.А., Тимофєєв, Г.А. Курсове проектування по теорії механізмів і машин / Попов С.А., Тимофєєв Г.А. – К, 2002.
6. Теорія механізмів машин: методич. вказівки й завдання до курсовому проекту / сост. Г.К. Семкина, А.А. Козик. – К., 1989.
7. Теорія механізмів і машин у прикладах і завданнях: Ч. 1. Структурне й кінематичне дослідження механізмів: посібник / А.А. Козик, И.С. Крук. – К., 2004.
8. Теорія механізмів, машин маніпуляторів / Филонов І.П., Анципорович П.П., Акулич В.К. – К., 1998.
© 2009 База Рефератов