
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Курсовая работа: Механизм насоса с качающейся кулисой
Курсовая работа: Механизм насоса с качающейся кулисой
Содержание
Введение
1 Синтез и анализ рычажного механизма
1.1 Структурный анализ механизма
1.2 Определение недостающих размеров
1.3 Определение скоростей точек механизма
1.4 Определение ускорений точек механизма
1.5 Диаграммы движения выходного звена
1.6 Определение угловых ускорений и скоростей
1.7 Определение ускорений центров масс звеньев механизма
1.8 Аналитический метод расчёта механизма
2 Силовой расчет рычажного механизма
2.1 Определение сил инерции
2.2 Расчет диады 4-5
2.3 Расчет диады 2-3
2.4 Расчет кривошипа
2.5 Определение уравновешивающей силы
2.6 Определение мощностей
2.7 Определение кинетической энергии и приведенного момента инерции механизма
3 Геометрический расчет зубчатой передачи. Проектирование планетарного механизма
3.1 Геометрический расчет зубчатой передачи
3.2 Определение передаточного отношения планетарной ступени и подбор чисел зубьев колес
3.3 Определение частот вращения зубчатых колес
4 Синтез и анализ кулачкового механизма
4.1 Диаграммы движения толкателя
4.2 Определение минимального радиуса кулачка
4.3 Построение профиля кулачка
Список использованных источников
Введение
Механизм насоса с качающейся кулисой применяется в нефтеперерабатывающей промышленности и предназначен для откачки жидкости нефтяных скважин.
Подача жидкости регулируется автоматически за счёт кулачкового механизма.
Поршень получает возвратно-поступательное движение в цилиндре от электродвигателя через планетарный редуктор и рычажный механизм О1АО2С.
При движении поршня вверх осуществляется рабочий ход, при движении поршня вниз - холостой.
При рабочем ходе на поршень 5 действует сила полезного сопротивления.
Механизм насоса с качающейся кулисой - одностороннего действия.
Кулачок 6 получает вращение посредством зубчатой передачи z5-z6.
1. Синтез и анализ рычажного механизма
Схема механизма:
Исходные данные:
Q=3450 H
H=240 мм
m3=42 кг
K=1,6
m5=35 кг
nкр=150 об/мин
O1O2=625 мм
nдв=1500 об/мин
1.1 Структурный анализ механизма
Степень подвижности механизма определим по формуле:
W=3n-2p1-p2;
Где n- число подвижных звеньев,
P1- число одноподвижных кинематических пар,
P2- число двуподвижных кинематических пар,
W=3·5-2·7-0=1
Разложение механизма на группы Ассура:
Формула строения механизма: I(0,1)→II(2,3)→II(4,5)
Механизм II класса, 2 порядка
1.2 Определение недостающих размеров
Угол размаха кулисы
b=180![]() = 180∙(1,6–1)/(1,6+1)=41,53
= 180∙(1,6–1)/(1,6+1)=41,53
Длину кривошипа определяем по формуле:
lO1A=0102 ∙sin![]() =0,625∙sin20,76=0,22м,
=0,625∙sin20,76=0,22м,
Длину lO2В определим по следующей формуле:
lO2В=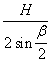 =0,24/2∙0,354=0.338 м,
=0,24/2∙0,354=0.338 м,
Выберем масштабный коэффициент
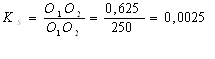
Строим 12 планов положений механизма, приняв за начало отсчета крайнее положение, соответствующее началу рабочего хода механизма.
1.3 Определение скоростей точек механизма
Определяем u точки А кривошипа:
uA=w1lO1A
где w1-угловая скорость вращения механизма, определяется по формуле:
w1=![]() =
=![]() рад/с,
рад/с,
Скорость точки А определим по формуле:
uA=ω1 O1A=15,71∙0,22=3,46 м/с,
План скоростей строим в масштабе:
ku=![]() =3,46/69,2=0.05
м∙с-1/мм
=3,46/69,2=0.05
м∙с-1/мм
Скорость точки A’ находим графически, решая совместно систему:
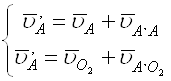
uA’= ku РuA’
По свойству подобия определяем скорость точки C’:
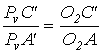
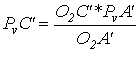
РVc’=136∙33/280=16мм
Абсолютное значение скорости точки
C’= ku puC’=0.05*17=0,85м/с
Составим систему уравнений скоростей для нахождения u в точке C:
uс’=uc’+ucc’
uc’=uc’c+uc’c
На плане puC=19мм. Абсолютное значение u в точке C:
uC= ku puC=0.05*19=0,95м/с.
Для остальных 11 положений скорости определяются аналогично, их значения приведены в таблице 1.1
Таблица 1.1 - Значения скоростей
| Скорости, м/с | Положение механизма | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| uА | 3,46 | 3,46 | 3,46 | 3,46 | 3,46 | 3,46 | 3,46 | 3,46 | 3,46 | 3,46 | 3,46 | 3,46 |
| uА’ | 1,65 | 2,95 | 3,4 | 3,4 | 3 | 2,15 | 0,7 | 1 | 2,9 | 3,15 | 1,7 | 0 |
| uC | 0,95 | 1,2 | 1,23 | 1,24 | 1,18 | 0,96 | 0,38 | 0,7 | 2,23 | 2,48 | 1,18 | 0 |
| uC’ | 0,85 | 1,24 | 1,29 | 1,26 | 1,18 | 0,96 | 0,37 | 0,65 | 2,14 | 2,42 | 1,16 | 0 |
1.4 Определение ускорений точек механизма
Ускорение точки А направлено по кривошипу к центру вращения О1.
aA=w12lO1A=15,712∙0.22=54,3м/с2
Выбираем масштабный коэффициент ускорений:
ka=![]() =54,3/108,6=0.25 м*с-2/мм
=54,3/108,6=0.25 м*с-2/мм
На плане ускорений изображаем ускорение точки А отрезком ![]() а=108 мм.
Ускорение точки А’ определяем, решая совместно систему
а=108 мм.
Ускорение точки А’ определяем, решая совместно систему
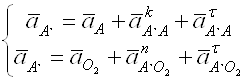
Для этого используем
aA’Ak=2∙w3 ∙VA’A=2∙VA’O2∙VA’A/A’O2=2∙Pva’∙aa’∙c/A’O2
c- коэффициент перечета определяется по формуле:
с=![]()
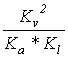 =0.052/(0.5∙0.0025)=2
=0.052/(0.5∙0.0025)=2
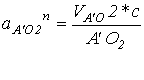
Ускорение точки С’ определим из соотношения:
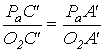
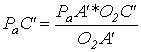
Ускорение точки С найдём, решая совместно систему
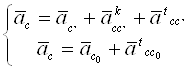
где
аCC’k=2·ω3·VCC’=2· РuA’·СС’·c/А’О2;
Ускорения всех точек механизма найдены. Ускорения для остальных положений механизма определяются аналогично. Значения ускорений сводим в таблицу 1.2.
Таблица 1.2- Значения ускорений.
| Ускорения, м/с2 | Положение механизма | ||||||
| 1 | 3 | 5 | 7 | 9 | 11 | 0 | |
| aA | 54,4 | 54,4 | 54,4 | 54,4 | 54,4 | 54,4 | 54,4 |
| aA’Ak | 14,37 | 7,74 | 12,02 | 7,55 | 24,7 | 23,56 | 0 |
| aA’O2n | 3,88 | 13,84 | 10,74 | 0,775 | 20,24 | 7,9 | 0 |
| ac’ | 15,3 | 5 | 7 | 24 | 40,6 | 48,1 | 32 |
| aCC’k | 0,75 | 0,5 | 1,25 | 0,00 | 3,45 | 1,9 | 0 |
| aC | 16,45 | 6,25 | 8,75 | 26,5 | 41,8 | 50,35 | 34 |
1.5 Диаграмма движения входного звена
Диаграмму перемещения S-t строим используя полученную из плана механизма траекторию движения точки С. Диаграммы скоростей V-t и ускорений а-t определяются из полученных 12-ти планов скоростей и планов ускорений.
Масштабные коэффициенты диаграмм
Кs=0.0025 (м/мм)
КV=0.05 (мс-1/мм)
Ка=0,5 (мс-2/мм)
1.6 Определение угловых скоростей и ускорений
ω1=![]() =3,14·150/30=15,71 (рад/с)
=3,14·150/30=15,71 (рад/с)
ω3=![]() =3,46/280·0,0025=4,94 (рад/с)
=3,46/280·0,0025=4,94 (рад/с)
ε1=0 (рад/с-2)
ε3=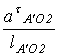 =14,88/280·0,0025=21,26
(рад/с-2)
=14,88/280·0,0025=21,26
(рад/с-2)
1.7 Определение ускорений центров масс звеньев механизма
Ускорения центров масс звеньев механизма определяем из планов ускорений.
aS'=Ka·РаS3=0.5*45=22,5 м/с2
Определяем относительные угловые скорости.
ω10= ω1=15,71 рад/с;
ω30= ω3=4,94 рад/с;
ω12= ω1- ω3=10,77 рад/с;
ω45= ω3=4,94 рад/с;
1.8 Аналитический метод расчёта механизма
Исходные данные:
![]() = 625 мм;
= 625 мм;
![]() = 15,71 рад/с;
= 15,71 рад/с;
![]() = 220 мм;
= 220 мм;
![]() = 41,530;
= 41,530;
![]() = 308 мм;
= 308 мм;
![]() = 20,760;
= 20,760;
Расчет ведется для первого положения кулисы:
![]() ;
;
В проекциях на координатные оси:
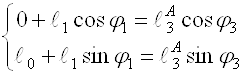 ;
;
Разделим второе уравнение ED Equation.3
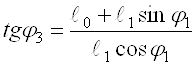 ;
;
Берем производную от левой и правой части:
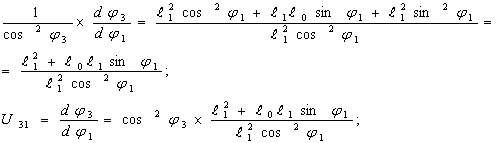
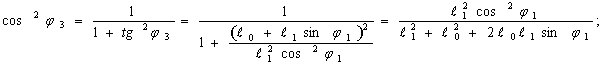
Угловая скорость кулисы:
![]()

Угловое ускорение кулисы:
![]()
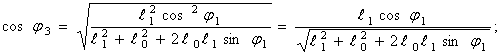
![]()
Составим векторное уравнение:
![]()
Проектируем на оси координат:
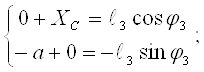
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Расчет скоростей и ускорений для первого положения механизма.
Угловая скорость кулисы:
![]()
![]()
Угловое ускорение кулисы:
![]() ;
;
![]()
![]() рад/с2 ;
рад/с2 ;
Скорость точки С :
![]() ;
;
![]() ;
;
![]() м/с;
м/с;
Ускорение точки C :
![]()
![]()
![]() ;
;
![]() рад/с2;
рад/с2;
2 Силовой анализ рычажного механизма
2.1 Определение сил инерции
Исходные данные:
w1=15,71 рад/с;
Q=3450 Н;
m5=35 кг;
m3’=12 кг;
m3’’=30 кг;
Определим силы инерции:
U5=-m5·aC;
U5= m5·PaC·Ka;
U5=35·30,6·0,5=535,5 (Н);
U3’=-m3’∙aS3’;
U3’=m3’·PaS’·Ka;
U3’=12·45·0,5=270 (Н);
U3’’=-m3’’∙aS3’’;
U3’’=m3’’·PaS’’·Ka;
U3’’=30·17·0,5=255 (Н);
Определим веса звеньев:
G5=m5·g;
G3’=m3’·g;
G3’’=m3’’·g;
G5=35·9,8=343,35 (Н);
G3’=12·9,8=117,72 (Н);
G3’’=30·9,8=294,3 (Н);
Сила полезного сопротивления Q=3450 Н.
Разбиваем механизм на группы Ассура в соответствии с формулой строения I(0,1)→II(2,3)→II (4,5). Начинаем силовой рассчёт самой удалённой от кривошипа диады.
2.2 Расчёт диады II (4,5)
Выделим из механизма диаду 4-5 и нагружаем её силами. Составляем уравнение равновесия диады 4-5:
∑Р(4,5)=, R50+Q+G5+U5+R43=0 (1)
Уравнение содержит два неизвестных- модули реакций R50 и R43, поэтому оно решается графически. Строим план сил по уравнению равновесия (1).
Для построения плана сил выбираем масштаб сил Кр
Кр=![]() =3450/172,5=20 н/мм
=3450/172,5=20 н/мм
Из плана сил определяем реакции:
R50= R50 Кр=66·20=1320 Н;
R43= R43 Кр=221·20=4420 Н;
2.3 Расчёт диады II (2,3)
Выделим диаду 2-3 и нагрузим её силами. Действие отброшенных звеньев 1,0 на третье заменяем действием реакций связей R21 и R30, которые требуется определить. Реакцию R21 направляем перпендикулярно линии движения ползуна, модуль неизвестен. Реакция R30 в шарнире О2 неизвестна ни по модулю ни по направлению; на схеме направляем её произвольно. Действие отброшенного звена 4 на третье известно: Реакция R34 равна по величине и противоположно направлена реакции R43, которая уже определена из плана сил диады II (4,5). Силы тяжести G3’ и G3’’ наносим на диаду в центрах масс стержней S3’ и S3’’. Силы инерции U3’ и U3’’ прикладываем в точках К’ и К’’, расположенных на расстоянии 2/3 длин стержней. Силы инерции направляем противоположно ускорениям центров масс согласно плана ускорений.
Составляем условия равновесия диады II(2,3):
∑Р(2,3)=0, R21+G3’+U3’+G3’’+U3’’+R34+R30=0 (2)
Данное уравнение содержит три неизвестных: модуль реакции R21, модуль и направление реакции R30. Значит уравнение (2) графически не решается. Реакция R21 может быть определена аналитически из уравнения моментов сил относительно точки О2.
∑М О2 (зв.2,3)=0, R21·AO2-U3’·hu3’+G3’·hg3’-U3’’·hu3’’-G3''·hg3’’-R34·O2C=0;
Откуда
R21= (U3’·hu3’- G3’·hg3’+ U3’’·hu3’’+ G3''·hg3’’+ R34·O2C)/ AO2
R21=(270·233-117,72·53+255·102-294,3·74+4500·132)/280=2539 Н
Теперь уравнение (2) содержит два неизвестных, а следовательно решается графически.
Строим план сил диады II(2,3) по уравнению (2). Считаем отрезки плана сил:
![]() = U3’/Кр=270/20=13,5 мм.
= U3’/Кр=270/20=13,5 мм.
![]() = U3’’/ Кр=255/20=12,75 мм.
= U3’’/ Кр=255/20=12,75 мм.
![]() = R21/ Кр=2539/20=126,95
мм.
= R21/ Кр=2539/20=126,95
мм.
![]() = G3’/ Кр=117,72/20=5,8
мм.
= G3’/ Кр=117,72/20=5,8
мм.
![]() = G3''/ Кр=294,3/20=14,7
мм.
= G3''/ Кр=294,3/20=14,7
мм.
Согласно уравнению (2) строим сумму векторов сил, откуда находим:
R30= ![]() ·Кр=274·20=5480 Н.
·Кр=274·20=5480 Н.
2.4 Расчёт кривошипа
Силовой расчёт кривошипа состоит в определении реакции стойки на кривошип R10 и уравновешивающей силы Ру, имитирующей действие силы со стороны двигателя.
Реакция R21 известна, так как R12= R21. Величина Рур определиться из уравнения моментов сил относительно точки О1 кривошипа.
∑М О1 (зв.1)=0, Рур·АО1-R12·hR12=0
Рур’= R12·hR12/ АО1=2539 40/88=1154 Н
Реакция стойки на кривошип R10 определиться из условия равновесия кривошипа:
![]() P(кр)=R21+Py+R10=0 (3)
P(кр)=R21+Py+R10=0 (3)
По уравнению (3) строим план сил кривошипа, откуда определяем искомую реакцию R10
R10= R10·Кр=110·20=2200 Н.
2.5 Определение уравновешивающей силы методом Жуковского
Уравновешивающую силу можно определить с помощью план скоростей по методу рычага Жуковского.
Строим повёрнутый на 90˚план скоростей и приложим к нему все внешние силы, действующие на механизм. План скоростей рассматриваем как жёсткий рычаг с опорой в полюсе. Рычаг находится в равновесии под действием приложенных сил.
Составляем уравнение равновесия рычага в форме суммы моментов сил в форме суммы моментов сил относительно полюса плана скоростей.
∑МPv1=0
Pyp’·Pva-(Q+U5+G5)·PvC-U3’’·hU3’’-G3’’·hG3’’-U3’·hU3’+G3’·hG3’=0
Pyp’=((Q+U5+G5)·PvC+ U3’’·hU3’’+ G3’’·hG3’’+ U3’·hU3’- G3’·hG3’)/ Pva
Pyp’=((3450+535,5+343,35)·47+255·33+294,3·24+270·69-117,72·13)/179
Pyp’=1173 Н
Сравниваем значения Pyp и Pyp’, найденные двумя способами
δ=( Pyp’- Pyp)/ Pyp’
δ=(1173-1154)·100%/1173=1,62%
2.6 Определение мощности
Мгновенная потребная мощность привода насоса без учёта потерь мощности на трение определяется соотношением:
Npy=Pyp·VA=1173·3,46=4058,58 Вт
Мощность привода, затраченная на преодоления только полезной нагрузки:
NQ=Q·Vc=3450·0,95=3277,5 Вт
Потери мощности во вращательных кинематических парах:
N10=R10·f’·(ω1-ω0)·rц=2200·0,132·15,71·0,025=114,5 Вт
N12=R12·f’·(ω1-ω3)·rц=2539·0,132·10,77·0,025=90,2 Вт
N30=R30·f’·(ω3-ω0)·rц=5480·0,132·4,94·0,025=89,3 Вт
N45=R45·f’·(ω3-ω5)·rц=4420·0,132·4,94·0,025=72,05 Вт
Где rц-радиус цапфы вала, rц=0,025 м,
f’- приведенный коэффициент трения, f’=(1,2…1,5)f=0,132
Потери мощности в поступательных кинематических парах:
N23=R23·f’·VA’A=2539·0,132·1,65=553 Вт
N34=R34·f’·VC’C=4420·0,132·0,85=495 Вт
N50=R50·f’·VC=1320·0,132·0,95=165,5 Вт
Суммарная мощность трения:
Nтр=∑Ni=N10+N12+N30+N45+N23+N34+N50
Nтр=114,5+90,2+89,3+72,05+553+495+165,5=1579,2 Вт
Мгновенная потребляемая мощность двигателя:
N=NРу+Nтр
N=4058,58+1579,2=5637,78 Вт
2.7 Определение кинетической энергии и приведенного момента инерции механизма
Кинетическая энергия механизма равна сумме кинетической энергии звеньев:
Тмех=∑Тi
Для механизма насоса с заданными параметрами кинетическая энергия звена равна:
∑Тi=Т3+Т5=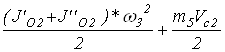
Где
JO2’=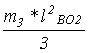 =12·0,352/3=0,49 кг·м2
=12·0,352/3=0,49 кг·м2
JO2’’=![]() =30·0,1552/3=0,24 кг·м2
=30·0,1552/3=0,24 кг·м2
Т3=(0,49+0,24)·4,942/2=8,9 Дж
Т5=35·0,95/2=16,62 Дж
Тмех=8,9+16,62=25,52 Дж
За звено приведения обычно выбирают ведущее звено. Так как у исследуемого механизма ведущим звеном является кривошип, то кинетическая энергия определится по формуле:
Tпр=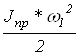
Откуда находим приведенный момент инерции:
Jпр=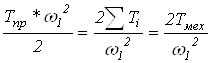
Jпр=2·25,52/15,712=0,2 кг·м2
3 Геометрический расчет зубчатой передачи. Проектирование планетарного механизма
3.1 Геометрический расчет зубчатой передачи
Исходные данные:
Число зубьев шестерни Z5=11;
Число зубьев колеса Z6=25;
Модуль m=6 мм;
Нарезание проводится методом обкатки инструментом
реечного типа, который профилируется на основе исходного контура по ГОСТ
13755-81 и имеет следующие значения: угол профиля ![]() ; коэффициент высоты головки
; коэффициент высоты головки ![]() ; коэффициент
радиального зазора
; коэффициент
радиального зазора ![]() ;
;
Определяем геометрические параметры эвольвентной передаче.
Определяем минимальный коэффициент смещения:
Z5<17и Z5+Z6≥34, следовательно, передача равносмещенная,
x5=(17-Z5)/17=(17-11)/17=0,35 мм;
x6=-x5=-0,35 мм;
Определяем делительное межосевое расстояние:
а= 0,5·m·(Z5+Z6)= 0.5·6·(11+25)=108 мм;
Определяем высоту зуба:
h=m(2ha*+c*)=6(2·1+0,25)=13,5 мм;
4) Делительная высота головки зуба:
ha=m·(ha*+x);
ha5= m·(ha*+x5)= 6·(1+0,35)= 8,1 мм;
ha6=m·(ha*+x6)=6·(1-0,35)= 3,9 мм;
5) Делительная высота ножки зуба:
hf= m·(ha*+C-x);
hf5= m·(ha*+C-x5)= 6·(1+0,25-0,35)= 5,4 мм;
hf6= m·(ha*+C+x6)= 6·(1+0,25+0,35)= 9,6 мм;
Диаметр делительной окружности:
d5= m·Z5= 6·11= 66 мм;
d6= m·Z6= 6·25= 150 мм;
Диаметр основной окружности:
db5= m·Z5·cos(α)= 6·11· cos(20)= 62,05 мм;
db6= m·Z6·cos(α)= 6·25· cos(20)= 147 мм;
Диаметр окружности вершин зубьев:
da=m·Z+2m·(ha*+x);
da5=m·Z5+2m·(ha*+x5)=6∙11+2·6(1+0,35)= 82,2 мм;
da6=m·Z6+2m·(ha*+x6)=6∙25+2·6(1-0,35)= 157,8 мм;
Диаметр окружностей впадин зубьев:
df=mZ-2m(ha*+C*-x);
df5=mZ5-2m(ha*+C*-x5)=11·5-2·6(1+0,25-0,35)=55,2 мм;
df6=mZ6-2m(ha*+C*-x6)=25·5-2·6(1+0,25+0,35)=130,8 мм;
10) Делительная окружная толщина зуба:
S=0,5·π·m+2m·x·tg(α);
S5=0,5·3,14·6+2·6·0,35·tg(20)= 10,9 мм;
S6=0,5·3,14·6-2·6·0,35·tg(20)= 7,9 мм;
Делительный шаг:
P= π·m = 3,14·6=18,84 мм;
12) Основной шаг:
Pb= π·m cos(α)= 3,14·6·0,94=17,7 мм;
13) Радиус кривизны галтели
ρ=0,38m=2.28 мм;
14) Строим зубчатую передачу с масштабным коэффициентом Kl=0,00025 м/мм;
15) Проверяем коэффициент торцевого перекрытия
а) аналитический метод:
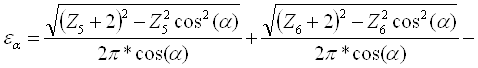
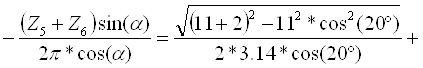
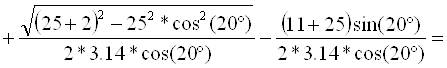 1,57
1,57
б) графический метод:
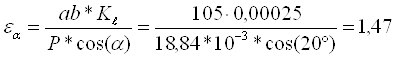
где ![]() – длина активной линии зацепления.
– длина активной линии зацепления.
3.2 Определение передаточного отношения планетарной ступени и подбор числа зубьев колес
Исходные данные:
nкр=150 мин-1;
nдв=1500 мин-1;
Z5=11;
Z6=25;
знак передаточного отношения привода (-)
Составляем общее передаточное отношение механизма:
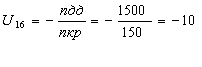
Рассчитаем передаточное отношение ![]() и
и ![]() через исходные данные:
через исходные данные:
![]()
Из исходного уравнения определяем передаточное отношение планетарной ступени:
![]()
![]() ;
;
Составляем формулу Виллиса для планетарной передачи:
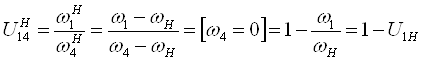 ;
;
![]()
![]() ;
;
Запишем через числа зубьев передаточное отношение обращенного механизма:
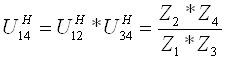 ;
;
Подбираем числа зубьев:
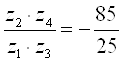 ;
; 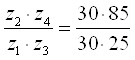 ;
;
Z1+Z2=Z4-Z3;
Z1+Z2=30+30=60
Z3+Z4=85-25=60
Z1=30, Z2=30, Z3=25, Z4=85
По выбранным числам зубьев определяем размеры колес:
d=m·Z;
d1=6·40=240 мм;
d2=6·40=240 мм;
d3=6·25=150 мм;
d4=6·85=510 мм;
d5=6·11=66 мм;
d6=6·25=150 мм
Масштабный коэффициент построения Кl=0,001 м/мм;
Для построения плана скоростей редуктора определяем скорость точки А:
![]() м/с;
м/с;
Строим план скоростей. Масштабный коэффициент плана скоростей
![]() мс-1/мм;
мс-1/мм;
3.3 Определение частот вращения зубчатых колес аналитическим методом
n1= nдв=1500 мин-1;
n6= nкр=150 мин-1;
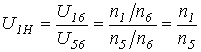 ;
;
![]() мин-1;
мин-1;
![]() ;
;
![]() мин-1;
мин-1;
![]() мин-1;
мин-1;
Значения частот вращения получим графическим методом:
![]() мин-1;
мин-1;
![]() мин-1;
мин-1;
![]() мин-1;
мин-1;
![]() мин-1;
мин-1;
4 Синтез и анализ кулачкового механизма
4.1 Диаграммы движения толкателя
Исходные данные:
Максимальный подъём толкателя h=29 мм;
Фазовый рабочий угол φ=290;
Дезаксиал е=0 мм;
nкр=150 об/мин;
Z5=11;
Z6=25
Угол давления α=25;
По заданному графику V-t графическим диференцированием получим график а-t, графическим интегрированием - S-t. Базы Н1=20 мм, Н2=25 мм. Методом исключения общего параметра t получим график V-S, a-S, a-V. Масштабные коэффициенты графиков:
Ks=![]() м/мм;
м/мм;
Kv=![]() мс-1/мм
мс-1/мм
Kt=![]() c/мм;
c/мм;
Ka=![]() мс-2/мм
мс-2/мм
4.2 Определение минимального радиуса кулачка
Минимальный радиус кулачка выбирается из условия выполнения угла давления. Для этого строим совмещённый график S’-V, где S’- текущее перемещение в стандартном масштабе КS’=0,0005 м/мм, V- аналог скорости.
На совмещённом графике на горизонтальных линиях откладываем аналоги скорости в масштабе КS’
x1=![]() мм
мм
x2=![]()
К совмещённому графику проводим две касательные под углом давления α. Ниже точки пересечения касательных выбирается центр вращения кулачка и соединяется с началом совмещённого графика. Это и будет минимальный радиус кулачка.
R0’=R0’·KS’=40·0,0005=0,02 м;
4.3 Построение профиля кулачка
Профилирование кулачка выполняется методом обращённого движения. Для этого строим кулачок в масштабе Кl=0,00025 м/мм. Проводим окружность радиусом R0’ и окружность радиуса е. Откладываем угол φр=290. Делим его на 12 частей и через точки деления проводим оси толкателя в обращённом движении. Вдоль осей толкателя откладываем текущее перемещение толкателя от окружности R0’. Соединяя полученные точки получим центровой профиль кулачка. Радиус ролика выбираем из условия:
rp=(0,2…0,4)R0’=0,25∙40=10 мм
Минимальный радиус действительного профиля:
R0=R0’-rp=40-10=30 мм
Обкатывая ролик по центровому профилю получаем действительный профиль.
Public Sub kul()
Dim I As Integer
Dim dis1, dis2, R, a1, a2, arksin1, arksin2, BETTA, BET As Single
Dim R0, FIR, FI0, FII, SHAG, E As Single
Dim S(1 To 10) As Single
R0 = InputBox("ВВЕДИТЕ МИНИМАЛЬНЫЙ РАДИУС КУЛАЧКА RO")
FIR = InputBox("ВВЕДИТЕ РАБОЧИЙ УГОЛ КУЛАЧКА FIR")
FI0 = InputBox("ВВЕДИТЕ НАЧАЛЬНОЕ ЗНАЧЕНИЕ УГЛА ПОВОРОТА КУЛАЧКА FI0")
E = InputBox("ВВЕДИТЕ ДЕЗАКСИАЛ E")
For I = 1 To 10
S(I) = InputBox("ВВЕДИТЕ СТРОКУ ПЕРЕМЕЩЕНИЙ S(" & I & ")")
Next I
FIR = FIR * 0.0174532
SHAG = FIR / 10
FI0 = FI0 * 0.0174532
FII = FI0
For I = 1 To 10
dis1 = (R0 ^ 2 - E ^ 2) ^ (1 / 2)
dis2 = S(I) ^ 2 + R0 ^ 2 + 2 * S(I) * dis1
R = dis2 ^ (1 / 2)
a1 = E / R
a2 = E / R0
arksin1 = Atn(a1 / (1 - a1 ^ 2) ^ (1 / 2))
arksin2 = Atn(a1 / (1 - a2 ^ 2) ^ (1 / 2))
BETTA = FII + arksin1 - arksin2
BETTA = BETTA * 180 / 3.1415
Worksheets(1).Cells(I, 1) = R
Worksheets(1).Cells(I, 2) = BETTA
FII = FII + SHAG
Next I
End Sub
Список использованных источников
1. Машков А.А. Теория механизмов и машин. Мн., 1971.
2. Артоболевский И.И. Теория механизмов и машин. М., 1975.
3. Фролов К.В., Попов С.А., Мусатов А.К. и др. Теория механизмов и машин под ред. К.В. Фролова М., 1986.
4. Попов С.А., Тимофеев Г.А. Курсовое проектирование по теории механизмов и механике машин. М., 1998.
© 2009 База Рефератов