
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Курсовая работа: Проект привода цепного конвейера
Курсовая работа: Проект привода цепного конвейера
Содержание
Вступление
1. Кинетический и силовой расчёт привода
1.1 Кинематическая схема привода
1.2 Выбор двигателя
1.3 Общее передаточное число и разбиение его по степеням
1.4 Силовые и кинематические параметры привода
2. Расчет клиноременной передачи
2.1 Исходные данные для расчёта передачи
2.2 Механический расчет
3. Расчет цилиндрической 3.1. Кинематическая схема передачи и исходные данные для расчета
3.2 Выбор материала и определение допустимых напряжений
3.3 Определение геометрических параметров
3.4 Проверочный расчет передачи
3.5 Определение сил в зацеплении (см. рис. 3.3)
4. Расчёт цилиндрической косозубой передачи || ступени
4.1 Кинематическая схема передачи и исходные данные для расчета
4.2 Выбор материала и определение допустимых напряжений
4.3 Определение геометрических параметров
4.4 Проверочный расчет передачи
4.5 Определение сил в зацеплении (см. рис. 3.3)
5. Условный расчет валов
5.1 Определение диаметров входного вала редуктора
6. Определение конструктивных размеров зубчатых колес
6.1 Размеры зубчатых колес цилиндрической передачи I ступени
6.2 Размеры зубчатых колес цилиндрической передачи II ступени
6.3 Определяем размеры цилиндрического колеса (рис.6.1.)
6.4 Определение диаметров выходного вала
7. Конструктивные размеры корпуса и крышки редуктора
7.1 Определение конструктивных размеров корпуса и крышки редуктора, согласно табл. 4.2, 4.3, [1]
7.2 Размеры необходимые для черчения
8. Выбор шпонок и их проверочный расчет
9. Расчёт промежуточного вала редуктора на статическую способность и долговечность
9.1 Расчет вала на несущую способность
9.2 Расчет вала на прочность
10. Расчет подшипников качения
10.1 Определение реакции в опорах
10.2 Определение коэффициентов
10.3 Определение эквивалентной нагрузки
10.4 Определяем долговечность подшипников
10.5 Выбор муфты
10.6 Проверочный расчёт зубчатой муфты
11. Выбор и проверочный расчёт опор скольжения
Литература
Вступление
Развитие народного хозяйства Украины тесно связано с развитием машиностроения, так как материальная мощность современной страны базируется на технике – машинах, механизмах, аппаратах, приводах, которые выполняют разную полезную работу. В наше время нет ни одной области народного хозяйства, где бы не применялись машины и механизмы в широких масштабах. Благодаря этому осуществляется комплексная механизация в промышленности, в сельском хозяйстве, в строительстве, на транспорте. Это заставляет уделять большое внимание при проектировании и усовершенствования конструкций современных машин и механизмов. Машины и механизмы, которые проектируются, должны иметь высокие эксплуатационные показатели, не большое количество энергии и эксплуатационных материалов, должны быть экономичными, как в процессе производства, так и в процессе эксплуатации, удобными и безопасными в обслуживании.
1. Кинетический и силовой расчёт привода
Согласно техническому заданию на курсовой проект по дисциплине «Детали машин» необходимо спроектировать привод цепного конвейера, который состоит из двигателя, клиноременной передачи, двухступенчатого цилиндрического ора и муфты. При проектировании деталей привода использованы современные критерии оценки их работоспособности – прочность, жесткость и износостойкость. Кинематический и силовой расчеты привода
1.1 Кинематическая схема привода
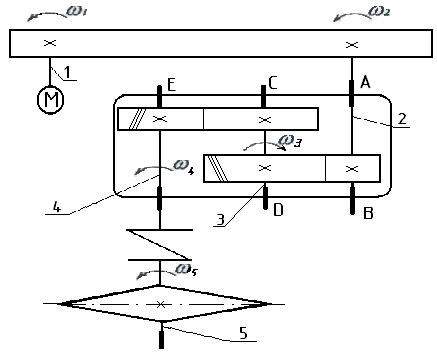
Рис 1.1
Таблица 1.1
Исходные данные для кинематического и силового расчета привода
| Название параметров | Обозначения в формулах | Единица измерения | Величина параметра |
| Окружная сила | F1 | Н | 28000 |
| Скорость |
|
м/с | 0,5 |
| Число зубьев | z | - | 9 |
| Шаг цепи | р | мм | 160 |
| Режим работы | P | - | С |
| Число смен | T | - | 1 |
1.2 Выбор двигателя
Работа над курсовым проектом по дисциплине «Детали машин» подготавливает студентов к решению более сложных задач общетехнического характера в своей дальнейшей практической деятельности.
Определяем необходимое усилие на валу 1 двигателя, кВт,
![]() кВт
кВт
где N5 усилие на приводном валу 5, кВт, ηобщ - общий кпд.
![]() кВт,
кВт,
ηобщ = η12η23 η34 η45 = 0,95· 0,95· 0,96· 0,98 = 0,85,
где η12= ηкр=0,95 кпд между 1 и 2 валами; η23= ηцп· η кр =0,96·0,99=0,95 – кпд между 2 и 3 валами; η34=ηцп· ηоп =0,97·0,99=0,96 – кпд между 3 и 4 валами; η45= ηм· ηоп ηоп=1·0,99·0,99=0,98 кпд между 4 и 5 валами.
Средние значения кпд принимаем из [1], табл. 1.1
ηкр =0,95-кпд клиноременной передачи;
ηцп =0,97-кпд цилиндрической передачи;
ηоп=0,99-кпд в опорах;
ηм=1,0-кпд муфты.
Принято, что валы привода установлены на подшипниках качения.
Определяем угловую скорость и частоту вращения вала электродвигателя.
![]() рад/с
рад/с
где ![]() рад/с – угловая скорость на 5
валу
рад/с – угловая скорость на 5
валу
где 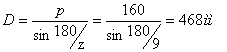
![]() - общее
передаточное отношение привода.
- общее
передаточное отношение привода.
![]() ,
,
Средние значения ориентировочных передаточных чисел принимаем из [2], табл. 5.5, с 74.
![]()
![]() - ориентировочное передаточное
число клиноременной передачи;
- ориентировочное передаточное
число клиноременной передачи; ![]() - ориентировочное передаточное
число цилиндрической передачи I ступени;
- ориентировочное передаточное
число цилиндрической передачи I ступени; ![]() - ориентировочное передаточное
число цилиндрической передачи II ступени;
- ориентировочное передаточное
число цилиндрической передачи II ступени; ![]() - ориентировочное передаточное
число муфты.
- ориентировочное передаточное
число муфты.
Определяем частоту вращения вала 1
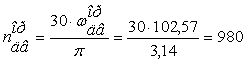 об/мин.
об/мин.
Выбираем электродвигатель исходя из условий ![]()
![]() .
.
Из [3], табл.2.4, с.23, выбираем электродвигатель 4АН180М6,
![]() кВт
кВт ![]() об/мин и для дальнейших
расчётов выполняем переход от
об/мин и для дальнейших
расчётов выполняем переход от ![]() к
к ![]()
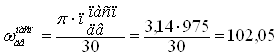 рад/с
рад/с
1.3 Общее передаточное число и разбиение его по степеням
Определяем действительное общее передаточное число привода при выбранном двигателе.
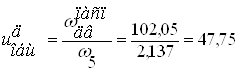
Проводим разбиение ![]() по
степеням.
по
степеням.
Принимаем ![]() ;
; ![]() ;
; ![]() .
.
Тогда 
1.4 Силовые и кинематические параметры привода
Определяем мощности на валах:
![]() кВт ;
кВт ; ![]() кВт ;
кВт ;
![]() кВт ;
кВт ; ![]() кВт;
кВт;
![]() кВт (див.розд.1.2.1.)
кВт (див.розд.1.2.1.)
Определяем угловые скорости валов:
![]() рад/с;
рад/с;
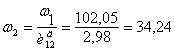 рад/с;
рад/с;
![]() рад/с;
рад/с;
![]() рад/с;
рад/с;
![]() рад/с.
рад/с.
Определяем крутящие моменты на валах:
![]() Нм;
Нм; ![]() Нм;
Нм;
![]() Нм;
Нм; ![]() Нм;
Нм;
![]() Нм.
Нм.
Результаты расчётов сводятся в табл.1.2 и являются исходными данными для всех следующих расчётов.
Таблица 1.2
Результаты кинетического и силового расчётов привода
|
Параметры вала |
N, кВт | ω рад/с | М,Нм |
|
|
|
| 1 | 16,5 | 102,05 | 161,7 | 2,98 | 47,68 | |
| 2 | 15,7 | 34,24 | 458,5 | |||
| 4 | ||||||
| 3 | 14,9 | 8,56 | 1740 | |||
| 4 | ||||||
| 4 | 14,3 | 2,14 | 6682 | |||
| 1 | ||||||
| 5 | 13 | 2,4 | 6542 |
2. Расчет клиноременной передачи
Схема клиноременной передачи
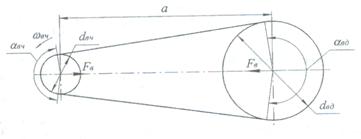
Рис 2.1
2.1 Исходные данные для расчёта передачи
Таблица 2.1
Исходные данные для расчета передачи
|
Параметры №шва |
N, кВт | w, рад/с | М, Нм | ид12 | и добщ |
| 1 | 16,5 | 102,05 | 161,7 | 2,98 | 47,68 |
| 2 | 15,7 | 34,24 | 458,5 |
2.2 Механический расчет
Сечение ремня по табл. 5.6 ([8], с. 69)
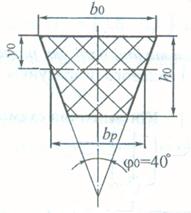
Рис 2.2
При заданном значении М принимаем сечение ремня (В).
Диаметр меньшего шкива
Минимально допустимый диаметр шкива dmin= 63 мм.
Для повышения коэффициента полезного действия передачи, увеличения долговечности и тяговой способности ремней, уменьшение числа ремней принимаем d1=100 мм.
Диаметр большего шкива: d2=d1·iкл =100∙2,98=298
Скорость ремня: ![]() ;
;
где v – скорость ремня, ![]() м/с.
м/с.
Частота вращения ведомого вала ![]() ;
;
где n2 – частота вращения ведомого вала, об/мин.;![]() - коэффициент
скольжения; принимаем
- коэффициент
скольжения; принимаем ![]() = 0,01
= 0,01
![]() об/мин.
об/мин.
Ориентировочное межосевое расстояние
Принимаем a0=400 мм.
Длина ремня
 ;
;
где L - длина ремня, мм;
![]() ;
;
![]() ;
;
![]() мм.
мм.
В соответствии с ГОСТ 1284.1-80 принимаем L = 1600 мм.
Окончательное межосевое расстояние
![]() ;
;
![]() мм.
мм.
Принимаем a = 500 мм.
Наименьшее расстояние, необходимое для надевания ремня
aнаим = a- 0,01L;
aнаим = 500-0,01·1600 = 484 мм.
Наибольшее расстояние, необходимое для компенсации вытяжки ремня
aнаиб = a- 0,025L;
aнаиб = 500-0,025·1600 = 460 мм.
Коэффициент динамичности и режима работы
ср = 1,1
Угол обхвата
![]() ;
;
где ![]() - угол обхвата, º;
- угол обхвата, º;
![]()
По табл. 5.7 ( 5, с.71) величина окружного усилия р0 , передаваемого одним ремнем р0=124 Н (на один ремень)
Допускаемое окружное усилие на один ремень
[р]=р0×Сα×СL×CР,
где Сα=1-0,003(180-α1)=1- 0,003(180-156,24)=0,93
Коэффициент, учитывающий длину ремня
![]() , так как расчетная длина L=1600=L0
, так как расчетная длина L=1600=L0
Коэффициент режима работы Ср=1, следовательно
[р]=824∙0,93=757
где р0 =814 ( по табл. 5,7 [8], с. 71 )
Окружное усилие
![]() Н
Н
Расчетное число ремней ![]() ;
; ![]() .
.
Принимаем Z = 4
3. Расчет цилиндрической 3.1. Кинематическая схема передачи и исходные данные для расчета
Кинематическая схема передачи
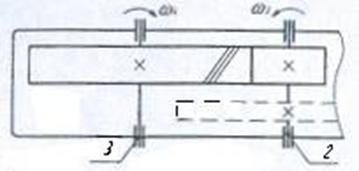
Рис.3.1.
Исходные данные для расчета передачи Таблица 3.1.
|
параметры вала |
N, кВт | ω, рад/с | M,Нм | ид34 | идобщ |
| 2 | 15,7 | 34,24 | 458,5 | 4,0 | 47,68 |
| 3 | 14,9 | 8,56 | 1740 |
3.2 Выбор материала и определение допустимых напряжений
Материалы зубчатых колес
Для уравновешивания долговечности шестерни и колеса, уменьшения вероятности заедания и лучшей приработки твердость зубьев шестерни необходимо выбирать большей, чем твердость колеса: НВш = НВк + (20…50).
Так как к габаритам передачи не накладываются жесткие условия, то для изготовления зубчатых колес, из [6], принимаем материалы для шестерни – сталь 50, для колеса – сталь 40. Параметры материалов зубчатых колес сводим в таблицу 3.2.
Таблица 3.2
Материалы зубчатых колес.
| Материал | Термообработка | Предел теку-чести, σт, МПа | Твердость, НВ | |
| Шестерня | Сталь 50 | нормализация | 380 | 180 |
| Колесо | Сталь 40 | нормализация | 340 | 154 |
Допустимые контактные напряжения:
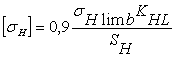 ,
,
где σНlim – граница контактной долговечности поверхности зубцов, соответствует базовому числу циклов изменения напряжений NН0 = 30 НВ2,4, (при твердости поверхности зубьев ≤350 НВ, σНlim b = 2 НВ +70):
σНlim bш = 2·180+70=430МПа, σНlim bк =2· 154 + 70=378 МПа;
NН0ш = 30·1802,4 = 7,76·106, NН0к = 30 · 1542,4 = 5,3·106;
SН коэффициент безопасности (запас прочности), учитывается от термообработки и характера нагрузок, принимаем SН = 1,1, [6];
КНL Коэффициент долговечности, который учитывает время службы и режим нагрузок передачи, определяется из соотношения NН0 и дополнения (NΣ·КНЕ); КНЕ – коэффициент интенсивности режима нагрузки, из [6], табл. 1.1, для легкого режима принимаем КНЕ = 0,06.
NΣ - суммарное число циклов нагрузки зубьев за все время службы передачи:
![]() ,
,
где Lh –время службы передачи, для односменной работы Lh=1·104 час.
![]() ,
, ![]() .
.
NΣш · КНЕ =1,96 · 108 · 0,06 = 1,17 · 106 < NН0ш = 7,76 · 106,
NΣк · КНЕ = 0,49 · 108 · 0,06 =2,9 · 106 < NН0ш = 5,3 ·106.
Так как в обоих случаях NН0 >NΣ · КНЕ , то коэффициент долговечности
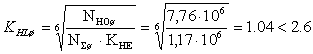 ,
,
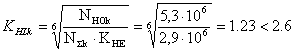 .
.
![]() Мпа;
Мпа; ![]() МПа
МПа
Допустимые напряжения на изгиб.
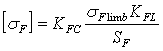 ,
,
где σFlimb граница выносливости поверхности зубцов при изгибе, соответствует базовому числу циклов смены напряжений NFо = 4 · 106, [6], (при твердости поверхности зубьев ≤350 НВ, σFlimb = НВ + 260):
σFlimbш = 180 +260 = 440МПа, σFlimbк = 154 + 260 = 414 МПа;
SF коэффициент безопасности (запас прочности), из [2], принимаем SF = 1,8, KFL – коэффициент долговечности, который учитывает время службы и режим нагрузок передачи, определяется соотношением NF0 и (NΣ KFЕ); KFЕ – коэффициент интенсивности режима нагрузки, из [6], табл. 1.1, для легкого режима принимаем KFЕ = 0,02.
NΣm· KFЕ = 1,05·108·0,02 = 2,1·106 < NF0 = 4·106,
NΣк · KFЕ = 0,26·108·0,02 = 0,52·106 < NF0 = 4·106.
Так как в обоих случаях NF0 > NΣ KFЕ, то согласно [ ], коэффициент долговечности:
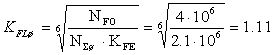 ;
; 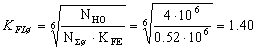 .
.
KFC - коэффициент реверсивности нагрузки, для нереверсивной передачи КНL – 1,0, [6].
![]() ;
; ![]()
Допустимые максимальные контактные напряжения.
[σН]max = 2,8 σТ.
[σН]max ш = 2,8·380 = 1064 МПа, [σН]max к =2,8·340=952 МПа.
Допустимые максимальные напряжения на изгиб.
[σF]max = 0,8 σТ.
[σF]maxш = 0,8·380 = 304 МПа., [σF]maxк = 0,8·340 = 272 МПа.
3.3 Определение геометрических параметров
Межосевое расстояние.
Из условий контактной усталости поверхности зубьев:
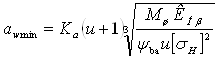 ,
,
где Ка – коэффициент межосевого
расстояния, из [6], для косозубых передач Ка = 4300 Па1/3;
![]() -
коэффициент ширины зубчатого венца по межосевому расстоянию, из [6], для
косозубой передачи принимаем
-
коэффициент ширины зубчатого венца по межосевому расстоянию, из [6], для
косозубой передачи принимаем
ψba = 0,45; и = ид34 = 4;
КНβ коэффициент распределения нагрузки по ширине венца зубчатого колеса, из [6], табл.1.2, в зависимости от ψbd = 0,5 ψba (и+1) = 0,5 · 0,45 · (4+1) = 1,13, для косозубой передачи КНβ = 1,046; [σН] – наименьшее из двух значений (шестерни и колеса) допустимых контактных напряжений, МПа.
 ,
,
![]()
Определение модуля.
Первоначальное значение расчетного модуля зубьев определяется
![]()
где β – угол наклона зубьев, для косозубой передачи β = 20°;
Zш число зубьев шестерни, согласно [6] принимаем Zш = 20;
Zш – число зубьев колеса, Zк = Zши = 20·4 = 80 .
Согласно [6], табл.1.3, принимаем mп = 5 мм.
- ширина: bк = ψdа аw = 0,45 · 266 = 119,7 мм. Принимаем bк = 120 мм.
3.4 Проверочный расчет передачи
Расчет на контактную усталость.
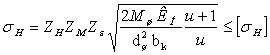
где ZН – коэффициент, учитывающий форму спряженных поверхностей зубьев: для косозубых - ZН = 1,75, [6];
ZМ = 275 · 103 Па1/2 - коэффициент учитывающий механические свойства материалов зубчатых колес, [6];
ZЕ - коэффициент суммарной длинны контактный линий спряженных зубьев: для косозубых - ZЕ = 0,8, [6];
КН = КНа КН β КНV – коэффициент нагрузки : КНа коэффициент распределения нагрузки между зубьями из [6], табл. 1.4, КН а = 1,15; КН β = 1,046, см. разд.3.3.1, КНV – коэффициент динамической нагрузки, из [6], табл. 1.4, при
![]() ; КHV=1.02;
КН=1,15∙1,046∙1,02=1,22.
; КHV=1.02;
КН=1,15∙1,046∙1,02=1,22.
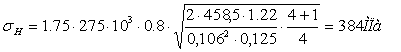
Так как σН = 363 находится в
пределах (0,9…1,0)[σН], то расчет можем считать завершенным: ![]() .
.
Расчет на контактную прочность.
![]() ,
,
где Кп=2,2, [σН]max наименьшее из двух значений (шестерни и колеса) допустимых максимальных контактных напряжений, МПа
![]()
Условие выполняется.
расчет на усталость при изгибе.
Определяем отдельно для шестерни и колеса по формуле
![]() ,
,
где - YF
- коэффициент формы зуба, из [6], табл. 1.7, по эквивалентному
числу зубьев ZV
, для косозубой
передачи: ![]() ,
YFш =3,92;
,
YFш =3,92; ![]() ,YFк =
3,6.
,YFк =
3,6.
YE - коэффициент перекрытия зубьев, согласно [6] принимаем YE =1,0.
Yβ -
коэффициент наклона зубьев, согласно [6] для косозубых передач принимается:![]()
КF = КFа К Fβ КFV- коэффициент нагрузки: КFа – коэффициент распределения нагрузки между зубьями для косозубых - КFа =1,0, [6], табл. 1,8; К Fβ –коэффициент
Геометрические размеры цилиндрической зубчатой передачи
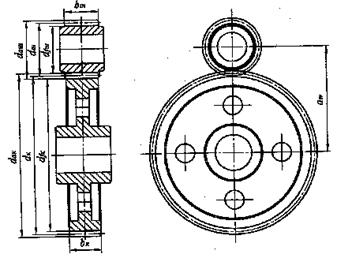
Рис 3.2.
Геометрический расчет передачи (см. рис. 3.2).
Межосевое расстояние
![]()
Принимаем аw = 266 мм.
Уточняем угол наклона зубьев
![]()
Размеры шестерни:
- делительный диаметр: ![]()
- диаметр вершин зубьев: dаш = dш + 2mn = 106,4+ 2 · 5= 116,4мм;
- диаметр впадин: dƒш = dш 2,5mn = 106,4 – 2,5 · 5= 93,9мм;
- ширина: bш = bк + 5 мм = 120 + 5 = 125 мм.
Размеры колеса:
-делительный диаметр ![]()
- диаметр вершин зубьев: dак = dк + 2mn = 425,5 +2 · 5 = 696 мм;
- диаметр впадин: dƒк = dк – 2,5mn = 425,5 – 2,5 · 5 = 413 мм;
распределения нагрузки по ширине венца зубчатого колеса, из [6], табл. 1.9, в зависимости от ψba = 1, 13 (см. разд. 3.3.1.) для косозубой передачи К Fβ = 1,09; КFV- коэффициент динамической нагрузки, выбирается из табл. 1.10, [6], при КFV = 1,05; КF = 1,00 · 1,09 · 1,05 = 1,14.
![]()
![]()
Условия выполняются.
Расчет на прочность при изгибе.
Выполняется отдельно для шестерни и колеса при действии кратковременных максимальных нагрузок (в период пуска двигателя).
σF maх = σF Кп ≤ [σF]max΄
где Кп – коэффициент перегрузки, из [2], табл. 1, с. 249 - Кп =2,2.
σF maх ш= 114 · 2,2 = 250,8 МПа ≤ [σF]max ш = 304 МПа,
σF maх к = 92 · 2,2 = 202,4 МПа ≤ [σF]max к = 272 МПа.
Условия выполняются.
3.5 Определение сил в зацеплении (см. рис. 3.3)
- окружная сила ![]()
- радиальная сила 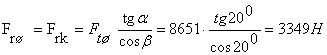
- осевая сила Fаш = Fак = Ftк tgβ = 8651· tg 19,95 0 = 3139 Н
Схема сил в зацеплении
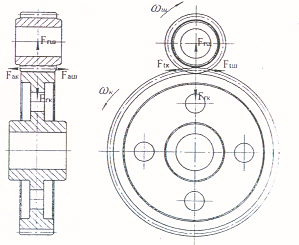
Рис.3.3.
4. Расчёт цилиндрической косозубой передачи || ступени
4.1 Кинематическая схема передачи и исходные данные для расчета
Кинематическая схема передачи
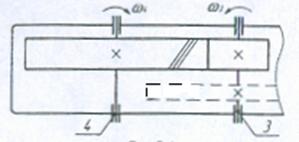
Рис.4.1.
Исходные данные.
Таблица 4.1.
Исходные данные для расчета передачи
|
параметры вала |
N, кВт | ω, рад/с | M,Нм | ид34 | идобщ |
| 3 | 14,9 | 8,56 | 1740 | 4 | 47,68 |
| 4 | 14,3 | 2,14 | 6682 |
4.2 Выбор материала и определение допустимых напряжений
Материалы зубчатых колес.
Для уравновешивания долговечности шестерни и колеса, уменьшения вероятности заедания и лучшей приработки твердость зубьев шестерни необходимо выбирать большей, чем твердость колеса: НВш = НВк + (20…50).
Так как к габаритам передачи не накладываются жесткие условия, то для изготовления зубчатых колес, из [6], принимаем материалы для шестерни – сталь 50, для колеса – сталь 40. Параметры материалов зубчатых колес сводим в таблицу 3.2.
Таблица 4.2.
Материалы зубчатых колес
| Материал | Термообработка | Предел теку-чести, σт, МПа | Твердость, НВ | |
| Шестерня | Сталь 50 | нормализация | 380 | 180 |
| Колесо | Сталь 40 | нормализация | 340 | 154 |
Допустимые контактные напряжения:
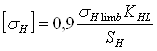 ,
,
где σНlim – граница контактной долговечности поверхности зубцов, соответствует базовому числу циклов изменения напряжений NН0 = 30 НВ2,4, (при твердости поверхности зубьев ≤350 НВ, σНlim b = 2 НВ +70):
σНlim bш = 2·180+70=430МПа, σНlim bк =2· 154 + 70=378 МПа;
NН0ш = 30·1802,4 = 7,76·106, NН0к = 30 · 1542,4 = 5,3·106;
KFL – коэффициент долговечности, который учитывает время службы и режим нагрузок передачи, определяется соотношением NF0 и (NΣ KFЕ); KFЕ – коэффициент интенсивности режима нагрузки, из [6], табл. 1.1, для легкого режима принимаем KFЕ = 0,02.
NΣm· KFЕ = 1,05·108·0,02 = 2,1·106 < NF0 = 4·106,
NΣк · KFЕ = 0,26·108·0,02 = 0,52·106 < NF0 = 4·106.
Так как в обоих случаях NF0 >
NΣ KFЕ,
то согласно [ ], коэффициент долговечности:
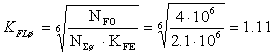 ;
;
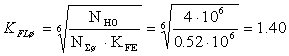 .
.
KFC - коэффициент реверсивности нагрузки, для нереверсивной передачи КНL 1,0, [6].
![]() ;
; ![]()
Допустимые максимальные контактные напряжения.
[σН]max = 2,8 σТ.
[σН]max ш = 2,8·380 = 1064 МПа, [σН]max к =2,8·340=952 МПа.
Допустимые максимальные напряжения на изгиб.
[σF]max = 0,8 σТ.
[σF]maxш = 0,8·380 = 304 МПа., [σF]maxк = 0,8·340 = 272 МПа.
4.3 Определение геометрических параметров
Межосевое расстояние.
Из условий контактной усталости поверхности зубьев:
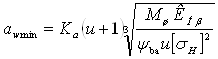 ,
,
где Ка – коэффициент межосевого
расстояния, из [6], для косозубых передач Ка = 4300 Па1/3;
![]() - коэффициент
ширины зубчатого венца по межосевому расстоянию, из [6], для косозубой передачи
принимаем
- коэффициент
ширины зубчатого венца по межосевому расстоянию, из [6], для косозубой передачи
принимаем
ψba = 0,45; и = ид34 = 4;
КНβ коэффициент распределения нагрузки по ширине венца зубчатого колеса, из [6], табл.1.2, в зависимости от ψbd = 0,5 ψba (и+1) = 0,5 · 0,45 · (4+1) = 1,13, для косозубой передачи КНβ = 1,046; [σН] – наименьшее из двух значений (шестерни и колеса) допустимых контактных напряжений, МПа.
 ,
,
![]()
Определение модуля.
Первоначальное значение расчетного модуля зубьев определяется
![]()
SН коэффициент безопасности (запас прочности ), зависит от термообработки и характера нагрузок, принимаем SН = 1,1, [6];
КНL Коэффициент долговечности, который учитывает время службы и режим нагрузок передачи, определяется из соотношения NН0 и дополнения (NΣ·КНЕ); КНЕ – коэффициент интенсивности режима нагрузки, из [6], табл. 1.1, для легкого режима принимаем КНЕ = 0,06.
NΣ - суммарное число циклов нагрузки зубьев за все время службы передачи:
![]() ,
,
где Lh –время службы передачи, для односменной работы Lh=1·10 4 час.
![]() ,
, ![]() .
.
NΣш · КНЕ =0,49 · 108 · 0,06 = 2,94 · 106 < NН0ш = 7,76 · 106,
NΣк · КНЕ = 0,12 · 108 · 0,06 = 0,72 · 106 < NН0ш = 5,3 ·106.
Так как в обоих случаях NН0 >NΣ · КНЕ , то коэффициент долговечности
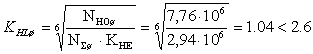 ,
,
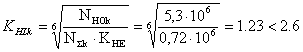 .
.
![]() Мпа;
Мпа; ![]() МПа
МПа
Допустимые напряжения на изгиб.
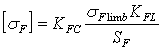 ,
,
где σFlimb граница выносливости поверхности зубцов при изгибе, соответствует базовому числу циклов смены напряжений NFо = 4 · 106, [6], (при твердости поверхности зубьев ≤350 НВ, σFlimb = НВ + 260):
σFlimbш = 180 +260 = 440МПа, σFlimbк = 154 + 260 = 414 МПа;
SF коэффициент безопасности (запас прочности), из [2], принимаем SF = 1,8,
где β – угол наклона зубьев, для косозубой передачи β = 20°;
Zш число зубьев шестерни, согласно [6] принимаем Zш = 20;
Zш число зубьев колеса, Zк = Zши = 20·4 = 80 .
Согласно [6], табл.1.3, принимаем mп = 8,0 мм.
- ширина: bк = ψdа аw = 0,45 · 425 = 191,25 мм. Принимаем bк = 220 мм.
4.4 Проверочный расчет передачи
Расчет на контактную усталость. распределения нагрузки по ширине венца зубчатого колеса, из [6], табл. 1.9, в зависимости от ψba = 1, 13 (см. разд. 3.3.1.) для косозубой передачи К Fβ = 1,09; КFV- коэффициент динамической нагрузки, выбирается из табл. 1.10, [6], при ν = 1,77 м/с, КFV = 1,05; КF = 1,00 · 1,09 · 1,05 = 1,14.
![]()
![]()
Условия выполняются.
Расчет на прочность при изгибе.
Выполняется отдельно для шестерни и колеса при действии кратковременных максимальных нагрузок (в период пуска двигателя).
σF maх = σF Кп ≤ [σF]max΄
где Кп – коэффициент перегрузки, из [2], табл. 1, с. 249 - Кп =2,0.
σF maх ш= 103 · 2,2 = 226,6 МПа ≤ [σF]max ш = 304 МПа,
σF maх к = 84 · 2,2 = 184,8 МПа ≤ [σF]max к = 272 МПа.
Условия выполняются.
4.5 Определение сил в зацеплении (см. рис. 3.3)
- окружная сила ![]()
- радиальная сила 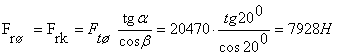
- осевая сила Fаш = Fак = Ftк tgβ = 20470 · tg20° = 7450 Н
Схема сил в зацеплении
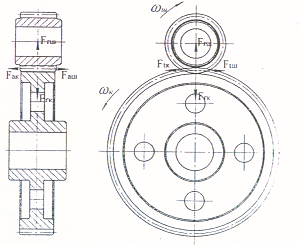
Рис.4.3.
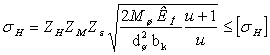
где ZН – коэффициент, учитывающий форму спряженных поверхностей зубьев: для косозубых - ZН = 1,75, [6];
ZМ = 275 · 103 Па1/2 - коэффициент учитывающий механические свойства материалов зубчатых колес, [6];
ZЕ - коэффициент суммарной длинны контактный линий спряженных зубьев: для косозубых - ZЕ = 0,8, [6];
КН = КНа КН β КНV – коэффициент нагрузки : КНа коэффициент распределения нагрузки между зубьями из [6], табл. 1.4, КН а = 1,15; КН β = 1,046, см. разд.3.3.1, КНV – коэффициент динамической нагрузки, из [6], табл. 1.4, при
![]() ; КHV=1.02;
КН=1,15∙1,046∙1,02=1,22.
; КHV=1.02;
КН=1,15∙1,046∙1,02=1,22.
![]()
Так как σН = 363 находится в
пределах (0,9…1,0)[σН], то расчет можем считать завершенным: 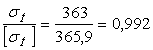 .
.
Расчет на контактную прочность.
![]() ,
,
где Кп=2,2, [σН]max наименьшее из двух значений (шестерни и колеса) допустимых максимальных контактных напряжений, МПа
![]()
Условие выполняется.
расчет на усталость при изгибе.
Определяем отдельно для шестерни и колеса по формуле
![]() ,
,
где - YF
- коэффициент формы зуба, из [6], табл. 1.7, по эквивалентному
числу зубьев ZV
, для косозубой
передачи: ![]() ,
YFш =3,92;
,
YFш =3,92; ![]() ,YFк =
3,6.
,YFк =
3,6.
YE - коэффициент перекрытия зубьев, согласно [6] принимаем YE =1,0.
Yβ -
коэффициент наклона зубьев, согласно [6] для косозубых передач принимается:![]()
КF = КFа К Fβ КFV- коэффициент нагрузки: КFа – коэффициент распределения нагрузки между зубьями для косозубых - КFа =1,0, [6], табл. 1,8; К Fβ –коэффициент
Геометрические размеры цилиндрической зубчатой передачи
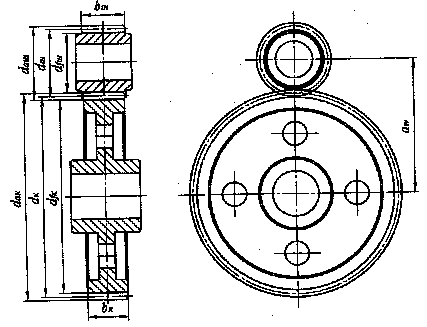
Рис 4.2.
Геометрический расчет передачи (см. рис. 4.2).
Межосевое расстояние
![]()
Принимаем аw = 425 мм.
Уточняем угол наклона зубьев
![]()
Размеры шестерни:
- делительный диаметр: ![]()
- диаметр вершин зубьев: dаш = dш + 2mn = 170 + 2 · 8,0 = 186мм;
- диаметр впадин: dƒш = dш 2,5mn = 170 – 2,5 · 8,0 = 150 мм;
- ширина: bш bк + 5 мм = 220 + 5 = 225 мм.
Размеры колеса:
-делительный диаметр ![]()
- диаметр вершин зубьев: dак = dк + 2mn = 680 +2 · 8,0 = 696 мм;
- диаметр впадин: dƒк = dк – 2,5mn = 680 – 2,5 · 8,0 = 660 мм;
5. Условный расчет валов
При отсутствии данных о моменте изгиба, диаметр вала определяют приблизительно по известному крутящему моменту из условий прочности на кручение по заниженным значениям допустимых напряжений:
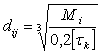
где i- номер вала, j- номер участка ступенчатого вала, Мi - крутящий момент на i-тому валу, принимаем из табл. 1.2. Согласно рекомендаций [4], с.53, принимаем пониженные допускаемые напряжения кручения, для валов редукторов общего назначения, [τк] = 25 МПа.
5.1 Определение диаметров входного вала редуктора
Схема входного вала редуктора
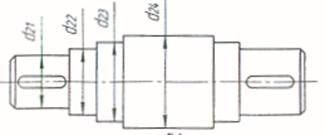
Рис. 5.1.
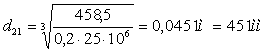
Согласно [7], с. 6 полученный диаметр округляем до ближнего большего значения из стандартного ряда Ra40 ГОСТ6636-69.
Принимаем d21 = 50 мм.
Диаметры других участков вала выбираем из стандартного ряда Ra40 ГОСТ6636-69.
Принимаем d22 =60 мм d23 = 60 мм d24 = 65 мм. .2. Определение диаметров промежуточного вала редуктора
Схема промежуточного вала редуктора
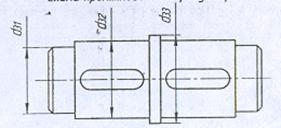
Рис. 5.1.
![]()
6. Определение конструктивных размеров зубчатых колес
6.1 Размеры зубчатых колес цилиндрической передачи I ступени
Устанавливаем способ изготовления шестерни и вала
вместе или отдельно. Согласно рекомендаций [1], если ![]() - отдельно,
- отдельно, ![]() – вместе, где dfш
- диаметр впадин шестерни (dfш
= 200,7 мм, см. разд.3.3.3.11), dвш
- диаметр участка вала под шестерню (dвш
= 60 мм, см. разд. 5.2)
– вместе, где dfш
- диаметр впадин шестерни (dfш
= 200,7 мм, см. разд.3.3.3.11), dвш
- диаметр участка вала под шестерню (dвш
= 60 мм, см. разд. 5.2)
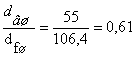 -выполняем вместе.
-выполняем вместе.
6.2 Размеры зубчатых колес цилиндрической передачи II ступени
Устанавливаем способ изготовления шестерни и вала
вместе или отдельно. Согласно рекомендаций [1], если ![]() - отдельно,
- отдельно, ![]() – вместе где dfш
– диаметр впадин шестерни,, dfш
=150 мм, dвш
- диаметр участка вала под шестерню dвш
= d24
=75 мм.
– вместе где dfш
– диаметр впадин шестерни,, dfш
=150 мм, dвш
- диаметр участка вала под шестерню dвш
= d24
=75 мм.
![]() - выполняется отдельно.
- выполняется отдельно.
6.3 Определяем размеры цилиндрического колеса (рис.6.1.)
Схема колеса зубчатого
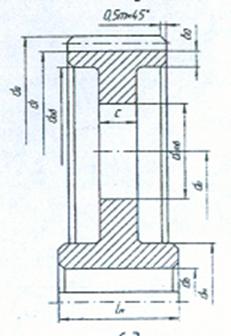
Рис.6.1.
Согласно [7], с.6 полученный диаметр округляем до ближайшего большего значения из стандартного ряда Ra40 ГОСТ6636-69.
Принимаем d31 = 70 мм.
Диаметры других участков вала выбираем из стандартного ряда Ra40 ГОСТ6636-69.
Принимаем d32 = 75 мм; d33 = 80 мм.
6.4 Определение диаметров выходного вала
Схема выходного вала редуктора
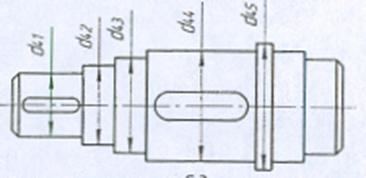
Рис. 5.2.
![]()
Согласно [7], с.6 полученный диаметр округляем до ближайшего большего значения из стандартного ряда Ra40 ГОСТ6636-69.
Принимаем d41 = 110 мм.
Диаметры других участков вала выбираем из стандартного ряда Ra40 ГОСТ6636-69.
Принимаем d42 = 115 мм; d43 = 120 мм; d44 = 130 мм. d45 = 140 мм.
Общая ширина зубчатого венца в=220 мм.
Диаметр ступицы dс = 1,6dв = 1,6 · 130 = 208 мм
Длина ступицы lс = (1,2…1,5) dв = 1,5 · 130 = 195 мм. Принимаем 220 мм
Толщина обода δ0 = (2,5…4)mn 4 · 8 = 32 мм
Толщина диска с = (0,2…0,4)b = 0,4·220 = 88 мм Принимаем 90 мм.
Диаметр отверстий в диске dотв = 0,25[dоб –(dв + 2 δст)],
где ![]() , dоб
= dfш
- 2 δ0 = 660 – 2 · 39 = 582 мм.
, dоб
= dfш
- 2 δ0 = 660 – 2 · 39 = 582 мм.
dотв = 0,25[582 –(130 + 2 ·39)] = 93,5 мм, принимаем dотв = 95 мм.
Диаметр центров отверстий в диске
d0 = 0,5(dв 2 δс + dоб) = 0,5 · (130 +2 · 38 + 582) = 395 мм.
7. Конструктивные размеры корпуса и крышки редуктора
7.1 Определение конструктивных размеров корпуса и крышки редуктора, согласно табл. 4.2, 4.3, [1]
Толщина стенки корпуса редуктора:
δ = 0,025aw + 3 = 0,025 · 425 + 3 = 13,6 ≈ 14 мм,
где aw межосевое расстояние зубчатых передач редуктора.
Толщина стенки крышки редуктора:
δ1 = 0,02аw + 3 = 0,02 · 425 + 3 = 11,5 ≈ 12 мм.
Толщина верхнего фланца корпуса:
S = (1,5…1,75) · δ =(1,5…1,75) ∙ 14 = 21…24,5 = 24 мм.
Толщина нижнего фланца корпуса:
S2 = 2,35 δ = 2,35 ∙ 14 = 32,9 ≈ 33мм.
Толщина фланца крышки редуктора:
S1 = (1,5…1,75) · δ1 =(1,5…1,75) · 12 = 18…21 = 20 мм.
Диаметр фундаментных болтов:
d1 = 0,072aw + 12 = 0,072 · 425 + 12 = 37,9 ≈ 39 мм,
Диаметр болтов, стягивающих корпус и крышку возле бобышек:
d2 = (0,7…0,75) · d1 =(0,7…0,75) ∙ 39 = 27,3…29,25 = 27 мм.
Диаметр болтов, стягивающих фланцы корпуса и крышки редуктора:
d3 = (0,5…0,6) · d1 =(0,5…0,6) ∙ 24 = 12…14,4 = 14мм.
Ширина опорной поверхности нижнего фланца корпуса:
m = k + 1,5 δ = 60 + 1,5 ∙ 14 = 81мм.
Толщина ребер корпуса:
с1 = (0,8…1) · δ = (0,8…1) ·∙ 14 = 10,4…14 = 12мм.
7.2 Размеры необходимые для черчения
Минимальный зазор между колесом и корпусом:
b = 1,2 δ = 1,2 · 14 = 16,8 мм.
Расстояние от внутренней стенки до торца вращающейся детали:
е1 = (1,0…1,2) ∙ δ = (1,0…1,2) ∙ 14 = 14…16,8 = 12мм.
Расстояние от внутренней стенки до радиального торца вращающейся детали:
е2 = (0,5…1,0) ∙ δ = (0,5…1,0) ∙ 14 = 7,0…14 = 10мм.
Расстояние от окружности выступов наибольшего колеса до дна редуктора: b0 = (0,5…10)m = (5…10) ∙ 8 = 50…80мм.
Размеры отверстий под подшипники редуктора принимаем в зависимости от размеров подшипника, согласно рекомендаций с. 141, [1].
Оставшиеся необходимые геометрические размеры корпуса и крышки принимаем конструктивно на основе рекомендаций с. 140-8. Эскизная компоновка редуктора
8. Выбор шпонок и их проверочный расчет
Выполняем проверочный расчет шпонки на смятие. Результаты расчетов сводим в таблицу 8.2.
Таблица 8.2.
Результаты проверочных расчетов шпонок на смятие
| Номер вала и название шпонки |
|
[σсм] |
| 2 шпонка под ведомый шкив клиноременной передачи |
|
140 |
| 2- шпонка под шестерню цилиндрической передачи I ступени |
|
|
| 3 шпонка под колесо цилиндрической передачи I ступени |
|
|
| 3 шпонка под шестерню цилиндрической передачи II ступени |
|
|
| 4 шпонка под колесо цилиндрической передачи II ступени |
|
|
| 4 шпонка под зубчатую муфту |
|
Схема шпоночного соединения
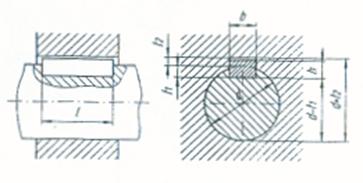
Рис. 8.1.
Для передачи крутящего момента зубчатые колеса, шкивы, муфты соединяются с валами при помощи призматических шпонок.
Геометрические размеры поперечных сечений (b, h) призматических шпонок выбираем в зависимости от диаметров валов. Длины шпонок принимаем на 5…10 мм меньше длин ступиц в ряду стандартных значений, приведенных в табл.5.19, [1].
В качестве материала шпонок используем – Сталь 45, нормализованную [σзм] = 140 МПа и [τзр] = 100 МПа, с. 191, [1].
Размеры сечений шпонок и пазов по ГОСТ 10748-79 выбираем из табл. 5.19, [1] и сводим в таблицу 8.1
Таблица 81
Параметры и размеры шпоночных соединений
| Номер вала и название шпонки | Диам. вала d1 мм |
Мкр, Нм |
Размеры шпонки, мм | ||||
| b | h | l | t1 | t2 | |||
| 2 шпонка под ведомый шкив клиноременной передачи | 50 | 458,5 | 18 | 11 | 80 | 7 | 4,4 |
| 2- шпонка под шестерню цилиндрической передачи I ступени | 55 | 458,5 | 20 | 12 | 90 | 7,5 | 4,9 |
| 3 шпонка под колесо цилиндрической передачи I ступени | 75 | 1740 | 22 | 14 | 100 | 9 | 5,4 |
| 3 шпонка под шестерню цилиндрической передачи II ступени | 75 | 1740 | 22 | 14 | 100 | 9 | 5,4 |
| 4 шпонка под колесо цилиндрической передачи II ступени | 130 | 6542 | 36 | 20 | 180 | 12 | 8,4 |
| 4 шпонка под зубчатую муфту | 110 | 6542 | 32 | 18 | 150 | 11 | 7,4 |
При эскизном проектировании размещаем детали передач (шестерни и зубчатые колеса), валы, подшипники, складываем эскизную компоновку цилиндрического редуктора.
По определенном размерам зубчатых передач, валов, корпуса и крышки(см. разд. 3, 4, 5, 6,) строим на миллиметровой бумаге формата А1 эскиз коническо – цилиндрического редуктора, в масштабе 1:4. При оформлении эскиза редуктора вычерчиваем конструкцию колес и его корпуса. Подшипники и болтовые соединения вычерчиваем упрощенно.
Подшипники качения выбираются из [3], ориентируясь на диаметры валов и характер нагрузки в передачах. В нашем случае выбираем подшипники №7312, №7314, №7224. В зависимости от их номера, который вмещает сведения о типе и серии подшипника выписываем габаритные размеры, которые используем в эскизной компоновке.
Размеры крышек под подшипники редуктора принимаем в зависимости от размеров подшипников, согласно рекомендаций с. 14.1, [1].
Другие необходимые геометрические размеры принимаем конструктивно, на основе рекомендаций с. 140-143, [1].
Для расчетов промежуточного вала из компоновочного чертежа прямым измерением определяем расстояние между точками приложения сил: l1 = 108мм, l2 = 184мм и l3 = 156мм.
После согласования параметров редуктора, проверочных расчетов валов и подшипников качения, чертим общий вид 143, [1].проверочный расчет шпонок на срез. Результаты вносим в таблицу 8.3.
Таблица 8.3
Результаты проверочного расчета шпонок на срез
| Номер вала и название шпонки |
|
[σсм] |
| 2 шпонка под ведомый шкив клиноременной передачи |
|
80 |
| 2- шпонка под шестерню цилиндрической передачи I ступени |
|
|
| 3 шпонка под колесо цилиндрической передачи I ступени |
|
|
| 3 шпонка под шестерню цилиндрической передачи II ступени |
|
|
| 4 шпонка под колесо цилиндрической передачи II ступени |
|
|
|
4 шпонка под зубчатую муфту |
|
Условия прочности на деформации смятия и срез выполняются.
Порядок построения сил выполняем в следующей последовательности:
- вычерчиваем кинематическую схему привода;
- обозначаем опоры валов латинскими буквами А, В, С, D, E, F, обозначаем точки приложения сил К1, К2, К3, К4, приводим пространственную систему координат X, Y, Z к которой осуществляется привязка действующих сил;
- выполняем построения схемы сил в точках их приложения, способность и долговечность
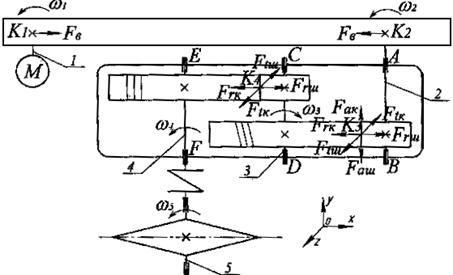
9. Расчёт промежуточного вала редуктора на статическую способность и долговечность
9.1 Расчет вала на несущую способность
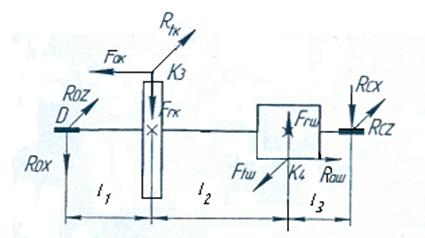
Силы, действующие на вал во время работы редуктора:
- силы, действующие на цилиндрическую шестерню II ступени: окружная сила Ftш = 20470 Н, Радиальная сила Frш =7928 Н; Осевая сила Faш =7450 Н.
- силы, действующие на цилиндрическое колесо I ступени Ftk = 8651 Н; радиальная сила Frk = 3349 Н; осевая сила Fак = 3139 Н.
Вычерчиваем расчетную схему вала (рис.9.1) и определяем размеры между опорами и точками приложения сил (расстояние определяем по первой эскизной компоновке редуктора измерением, допустив, что силы приложенные по середине колеса и шестерни): l1 = 108 мм, l2 = 184 мм, l3 = 156 мм.
Находим реакции в опорах от сил в вертикальной и горизонтальной плоскости:
- в вертикальной х0у
ΣМF(D) =0.
![]() .
.

RDX = RCX –Frш +Frk = 7262 - 7928 + 3349 = 2683 Н
- в горизонтальной zOx
ΣМF(D) =0
ΣМF(D) = - Ftш ∙(l1+l2)+ Ftk ∙l1+ Rc z (l1 + l2 +l3 ) = 0
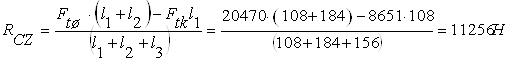
RDZ = - Rc z + Ftш + Ftk = - 11256 + 20470 – 8651 = 562Н
Выполняем построения эпюр моментов изгиба в вертикальной и горизонтальной плоскостях, суммарного крутящего момента и изгиба.
Момент изгиба в вертикальной плоскости:
в m.K3: МК3 = RDX · l1 = 2683 · 0,108 = 290 Нм;
в m.K4: МК4 = RCX · l3 = 7262 · 0,156 = 1132,8 Нм;
Момент изгиба в горизонтальной плоскости
в m.K4: МК4 = RDz · l1 = 562 · 0,108 = 61Нм;
Суммарный момент изгиба определяется по формуле:
в m.K3:
![]()
в m.K4:
![]()
Определяем приведенный (эквивалентный) момент в опасном сечении.
Исходя из анализа построенных эпюр моментов опасное сечение вала находится на шестерне цилиндрической передачи II ступени (точка К4).
Значение эквивалентного момента в m.K4:
![]() .
.
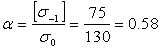
– коэффициент, табл. 5.3., [1] для материала вала
– сталь 40. [σ1], σ0 - допустимые напряжения для материала вала соответственно при симметричном и при пульсирующем циклах нагрузки, табл. 5.3., [1].
![]()
Определяем диаметр вала в опасном сечении:

Полученный диаметр округляем до ближайшего большего значения из стандартного ряда Rа 40 ГОСТ 6636-69. С учетом шпоночного паза принимаем d32 = 75мм.
Диаметр вала в этом сечении, принятый в условном расчете
d32 = 75,0мм, т.е. условие выполняется.
9.2 Расчет вала на прочность
Для опасного сечения быстроходного вала, который имеет конструктивный концентратор напряжений – переход от меньшего диаметра к большему (между участками под подшипник и шестерню), определяем характеристики напряжений, [1], с.173- 185.
- границы выносливости:
для напряжений изгиба при симметричном цикле:
σ-1 = 043σВ =0,43 · 800 = 344 МПа, σm = 0 МПа;
для напряжений кручения при пульсирующем цикле:
τ-1 = 0,58 σ-1 = 0,58 · 344 = 199,52 МПа; τm = τа =2,79 МПа;
-амплитуды напряжений:
при симметричном цикле:
![]()
где МЗj – суммарный момент изгиба в m. К4, Нм,
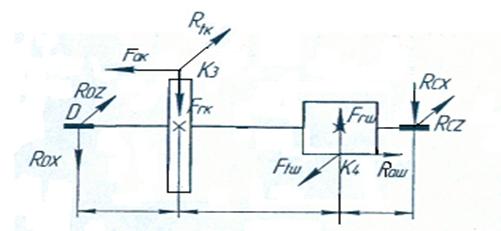
Рис. 11 .1.
Зj – осевой момент в сечении опор j – того участка вала. Для сечения в m. К4, м3.
![]()
где d – диаметр вала под подшипник,
при пульсирующем цикле:
![]()
где W кj – полярный момент сечения опор j – того участка вала. Для сечения под шпонку, м3.
![]()
Выбираем коэффициенты:
- эффективные коэффициенты конструкционных напряжений при изгибе - Кσ = 1,75, при кручении - Кτ =1,50, табл. 5.11, [1].
- масштабные коэффициенты, учитывающие снижения границы выносливости с увеличением размеров вала: при изгибе - έσ = 0,745; при кручении- έr = 0,745, табл. 5.16, [1].
- коэффициенты учитывающие свойства материалов до асимметрии цикла напряжений:
при изгибе – ψσ =0,02 + 2·10-4 · 800 = 0,18 МПа;
при кручении - ψτ =0,5ψσ = 0,5· 0,18 = 0,09 МПа.
Определяем коэффициент запаса прочности опасного сечения:
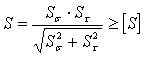
где Ѕσ и Ѕτ коэффициенты запаса прочности при действии изгиба и кручения.
[Ѕ] –допустимое значение коэффициенты запаса прочности. Для редукторных валов [Ѕ] ≥2,5…3,0, с.185, [1].
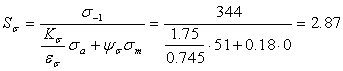 ,
,
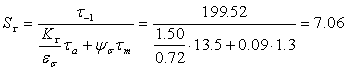 ,
,
![]()
Условие выполняется.
10. Расчет подшипников качения
Исходные данные для расчета:
Диаметры вала под подшипники – 70 мм
Реакции в опорах: Rсх = 7262 Н, RDX =2683Н,
RCZ=11256, ROZ=562H
Осевые силы: Fфш = 7450 Н, Fок = 3139Н.
Угловая скорость: ω3 =18,3 рад/с.
Pис. 12.1
10.1 Определение реакции в опорах
Определяем результативную радиальную реакцию в каждой опоре вала (для схемы нагрузки):
![]() ,
,
где Rпх = Rnz – радиальные реакции в опоре, в горизонтальной и вертикальной плоскостях.
Индекс «п»- опора.
![]() ;
;
![]() .
.
Выбираем роликовые однорядные подшипники №7314 с такими основными параметрами:
d = 70 мм, D = 150 мм, B = 35 мм.
C = 168 кН – динамическая грузоподъемность;
С0 = 137 кН – статическая грузоподъемность;
е = 1,5tga =1,5 tg140 = 0,37.
Результирующая осевая сила:
Fa = Fаш Fак = 7450 –3139= 1713 Н.
Определяем по соотношению ![]() коэффициент осевой нагрузки.
коэффициент осевой нагрузки.
Определяем составляющие осевых реакций Sп в подшипниках от радиальных реакций Rrn:для радиально-упорных шариковых подшипников:
- для опоры А:
SC=eRrC=0.37∙13395=4956H;
для опоры В:
SD=eRrD=0.37∙2741=1014.0H.
Определение осевых реакций Rап подшипников.
Осевые реакции определяем исходя из схемы размещения
подшипников, принимаем схему – «в распор»:
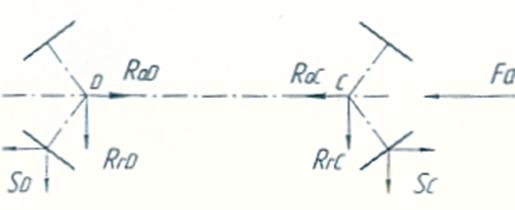
Рис.10.2.
-в т. D
ΣF=-SC+Fa+SD=-4956+4311+1014=369H>0.
тогда
RaD=Fa+SC=4311+4956=9267H
-в т. С
ΣF=-SD-Fa+SC=-1014-4311+4956=-369H.>0
тогда
RaC=SC=4956H.
10.2 Определение коэффициентов
V-коэффициент оборота кольца, V=1,0 (вращается внутреннее кольцо);
реакции подшипников:
- для опоры С
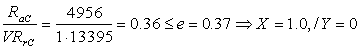
- для опоры D
![]()
10.3 Определение эквивалентной нагрузки
Pen=(X∙V∙Rrn+Y∙Ran)∙KσKT :
- опора С: РеС=(1∙1∙13395+0∙4956)∙1,3∙1,0=17413,5Н;
- опора D: PeD=(0.4∙1∙2741+1.88∙9267)∙1.3∙1.0=24074H.
10.4 Определяем долговечность подшипников
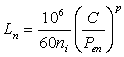 ,
,
где пi- частота вращения i-того вала, об/мин,
![]() .
.
р=10/3- для роликовых подшипников.
Опора С: 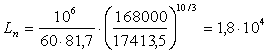 ч,
ч,
Опора D:
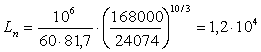 ч,
ч,
Срок работы привода Lh=1∙104ч подшипники (опора С и опора D) обеспечивают.
10.5 Выбор муфты
Расчётный крутящий момент, который передаёт муфта в данном приводе определяется по формуле:
Мmax=KPMн=1,5∙6682=10023Нм,
где KP = 1,5 – коэффициент, который учитывает условия эксплуатации установки, принимаем по табл. 7.1. , [1].
Мн – номинальный крутящий момент на валу.
Выбираем зубчатую муфту МЗ 6, табл. 17.6.,[9] с такими параметрами:
М=11800 Нм, dв = 105 мм, nmax=2500 об/мин.
Геометрические размеры муфты, см. рис. 12.2.
B = 50 мм, D=320 мм, D1=230 мм, D2=140 мм, L=255 мм.
Размеры зацепления зубчатой муфты:
m =4,0 мм, z=48, b=30 мм.
Муфты зубчатые используют для соединения валов, которые передают большие крутящие моменты, где точное установление валов невозможно или возникают значительные осложнения. Зубчатые муфты отличаются компактностью и высокой выносливостью нагрузок.
Компенсирующая способность муфты достигается созданием зазоров между зубьями и приданием бочкообразной формы зубьям.
10.6 Проверочный расчёт зубчатой муфты
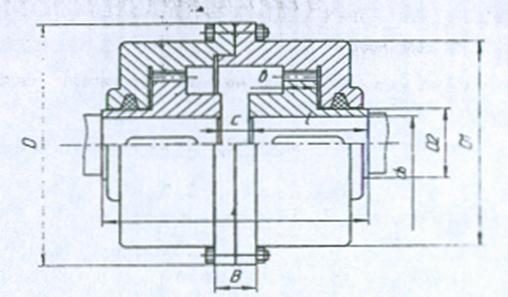
Рис. 10.5.
11. Выбор и проверочный расчёт опор скольжения
В качестве опор конвейера принимаем подшипники
скольжения, разъёмные с двумя болтами по ГОСТ 11607-65 с чугунными вкладышами с
СЧ 18 для которого определяем допустимые значения параметров: ![]() ,
, ![]() , табл. 9.1, [8].
, табл. 9.1, [8].
Конструктивные размеры корпуса выбранного подшипника определяем согласно С.594, [8] в зависимости от диаметра вала:
dВ=110 мм, d1=32 мм, B=130 мм, b=110 мм, H=200 мм, h=110 мм, h1= 40 мм, L=370 мм, A=310 мм,
A1=190 мм, шпилька М24х100.
Схема подшипника скольжения
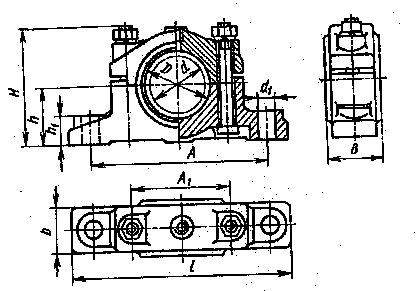
Рис. 11.1.
Проверяем выбранный подшипник по двум критериям:
- условие износа ( долговечность )
![]() ,
,
где F0=Ft=28000 H – окружная сила, см. раздел 1.1.
- условие теплоустойчивости
![]()
где ![]() - скорость скольжения.
- скорость скольжения.
Оба условия выполняются, значит опоры скольжения удовлетворяют
При проверочном расчёте у зубчатых муфт рассчитывают рабочие поверхности зубов на износ (определяется граничное значение удельного давления на зубцы муфты).
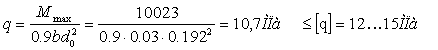
где d0 диаметр делительного круга, м, d0 = mz=4,0∙48=192 мм, b – длина зуба зубчатой втулки, м, [q] – допустимое значение удельного давления для материала зубов, МПа, табл. 17.6, [9].
Литература
1. Киркач Н.Ф., Баласанян Р.А.. Расчёт и проектирование деталей машин [Учеб. Пособие для техн. вузов]. – 3-е изд., перераб. и доп. – Х.: Основа,1991.- 276 с.: схем.
2. Расчёты деталей машин: Справ. Пособие / А.В. Кузьмин, И.М. Чернин, Б.С. Козинцов. – 3-е изд., перераб. и доп. – Мн.: Выс. шк., 1986. – 400 с.: ил.
3. Курсовое проектирование деталей машин: Справ. Пособие. Часть 1 / А.В. Кузьмин, Н.Н. Макейчик, В.Ф. Калачев и др.-Мн.: Выс. школа ,1982-208 с.,ил.
4. Курсовое проектирование деталей машин: Справ. Пособие. Часть 2 / А.В. Кузьмин, Н.Н. Макейчик, В.Ф. Калачев и др.-Мн.: Выс. школа ,1982-334 с.,ил.
5. Методичн вказівки для виконання курсового проекту з курсу „Деталі машин” (Розділ „Пасов передачі ”) для студентів спец. 31.11 заочної форми навчання / Гончарук О.М., Стрілець В,М., Шинкаренко І.Т., - Рівне, У||ВГ, 1990.-24 с.
6. Методические указания по выполнению курсового проекта по курсу «Детали машин» (Раздел «Расчёт закрытых зубчатых и червячных передач») для студентов специальности 1514 заочной формы обучения / Стрелец В.Н,, Шинкаренко И,Т.- Ровно, УИИВГ, 1988 41 с.
7. Методичн вказівки для виконання курсового проекту з курсу „Деталі машин” (Розділ Розрахунки валів і підшипників кочення”) для студентів спец. 31.11 заочно форми навчання / Стрілець В,М., Шинкаренко І.Т., - Рівне, У||ВГ, 1990.-16 с.
С.А. Чернавский, Г.М. Ицкович и др.. Курсовое проектирование деталей машин, М: Машиностроение, 1979-351
© 2009 База Рефератов