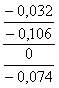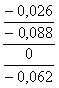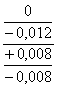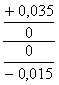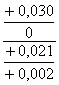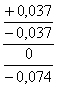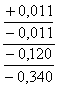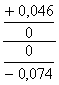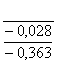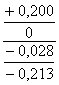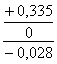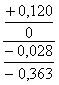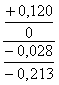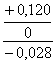Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Курсовая работа: Расчет подшипников качения для червячной передачи
Курсовая работа: Расчет подшипников качения для червячной передачи
Задание
1 Описание конструкции и назначение узла
2 Расчет и выбор посадок подшипников качения
3 Выбор посадок для сопряжений узла и их расчёт
4 Выбор средств измерений деталей
5 Расчёт рабочих и контрольных калибров
6 Расчёт и выбор посадки с натягом
7 Расчёт точности зубчатой передачи
8 Расчёт и выбор посадки с зазором
9 Расчёт размерной цепи вероятностным методом
Список используемых стандартов
1 Описание конструкции и назначения узла.
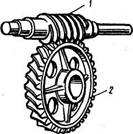
Червячной передачей называется механизм, служащий для преобразования вращательного движения между валами со скрещивающимися осями. Обычно червячная передача (рис.1) состоит из червяка 1 и сопряженного с ним червячного колеса 2. Угол скрещивания осей обычно равен 90°; неортогональные передачи встречаются редко. Червячные передачи относятся к передачам зацеплением, в которых движение осуществляется по принципу винтовой пары. Червячную передачу можно получить из рассмотренной ранее винтовой зубчатой передачи, если уменьшить число зубьев одного из косозубых колес до z1= 1...4 и увеличить их угол наклона к оси, превратив таким образом косозубое колесо в винт (червяк). Поэтому червячные передачи относят к категории зубчато-винтовых.
Все применяемые в дальнейшем термины, определения и обозначения, относящиеся к червячным передачам, соответствуют ГОСТ «Передачи червячные» и ГОСТ «Передачи зубчатые».
Витки червяка и зубья червячного колеса соприкасаются обычно по линиям и поэтому представляют собой высшую кинематическую пару. Обычно ведущее звено червячной передачи — червяк, но существуют механизмы, в которых ведущим звеном является червячное колесо.
Достоинства червячных передач: компактность конструкции и возможность получения больших передаточных чисел в одноступенчатой передаче (до u = 300 и более); высокая кинематическая точность и повышенная плавность работы; малая интенсивность шума и виброактивности; возможность обеспечения самоторможения.
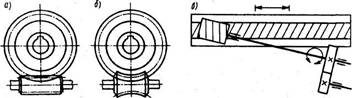
На рис.2 схематически изображены основные виды червячных передач:
а — цилиндрическая червячная передача, у которой делительные и начальные поверхности цилиндрические (такие передачи имеют наибольшее распространение); б — глобоидная передача, у которой делительная поверхность червяка торообразная, а колеса цилиндрическая (такие передачи нетехнологичны); в— червячно-реечная передача (по сравнению с зубчато-реечной такай передача обеспечивает большую плавность работы и имеет большую жесткость; оси червяка и рейки могут располагаться под углом или быть параллельны; передачи применяют в продольно-строгальных, тяжелых фрезерных и горизонтально-расточных станках).
Недостатки червячных
передач:
значительное геометрическое скольжение в зацеплении и связанные с этим трение,
повышенный износ, склонность к заеданию, нагрев передачи и сравнительно низкий
КПД (от ![]() до
до ![]() ); необходимость применения
для ответственных передач дорогостоящих и дефицитных антифрикционных цветных
металлов. Указанные недостатки ограничивают мощность червячных передач (обычно
); необходимость применения
для ответственных передач дорогостоящих и дефицитных антифрикционных цветных
металлов. Указанные недостатки ограничивают мощность червячных передач (обычно
до 60 кВт).
Червячные передачи находят широкое применение, например, в металлорежущих станках, подъемнотранспортном оборудовании, транспортных машинах, а также в приборостроении.
Витки червяка нарезают резцом на токарно-винторезном или дисковой фрезой на резьбофрезерном станке; после нарезания резьбы и термообработки рабочие поверхности витков нередко шлифуют и полируют, что существенно повышает нагрузочную способность передачи. Зубья червячного колеса нарезают методом обкатки червячными фрезами на зубофрезерных станках; режущий инструмент в этом случае подобен червяку, снабженному режущими кромками и гранями (производящий червяк). Такая технология изготовления обеспечивает линейный контакт между витками червяка и зубьями червячного колеса.
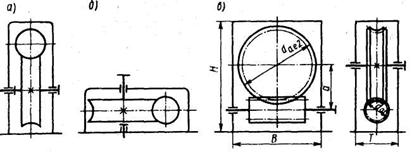
Для цилиндрических червячных передач установлено двенадцать степеней точности и соответствующие нормы точности изготовления и монтажа передач. Независимо от степени точности передач назначают нормы бокового зазора между витками червяка и зубьями колеса.
Для глобоидных передач установлено три степени точности: 6, 7 и 8, для каждой из которых назначают нормы точности изготовления червяка, колеса и монтажа передач. Независимо от степени точности устанавливают нормы бокового зазора.
Силовые червячные передачи обычно изготовляют по 6—8-й степеням точности.
Конструктивно червячные передачи чаще всего делают в закрытом исполнении. На рис.3 приведены схемы наиболее часто встречающихся червячных редукторов: а — с верхним расположением червяка, б — с боковым расположением червяка, в — с нижним расположением червяка.
2 Расчёт и выбор посадок подшипников качения
Исходные данные:
Подшипник №7210
Класс точности 0
Радиальная реакция R = 1,6 kH
Осевое усилие A = 2 kH
Характер нагрузки - с умеренными толчками и вибрациями, перегрузка до 150%.
Размеры подшипника [2]:
![]()
![]()
![]()
![]()
![]()
2.1 Для циркуляционно нагруженного кольца определяется интенсивность нагружения PR, H.
![]() , (2.1)
, (2.1)
где R – радиальная реакция опоры на подшипник, кН
В – ширина подшипника, мм
r – радиус фасок колец подшипника, мм
KП – динамический коэффициент посадки [1,табл.3.5]
F – коэффициент ослабления посадочного натяга при полом вале или тонкостенном корпусе FA – коэффициент неравномерности распределения радиальной нагрузки между рядами роликов или между сдвоенными шарикоподшипниками при наличии осевой нагрузки на опору [1,табл. 3.2]
![]()
![]()
2.2 По величине интенсивности нагружения PR выбираем вид посадки [1,табл.3.6,]
«![]() » - посадка на вал
» - посадка на вал
2.3 Для колец, воспринимающих колебательное и местное нагружение, выбирается вид посадки в зависимости от характера нагружения и вида корпуса [1, табл. 3.3]
«H» - посадка в корпус
2.4 Выбор квалитета для посадок колец подшипников
Для вала – 6 квалитет
Для корпуса – 7 квалитет
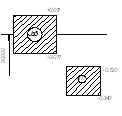
2.5 По ГОСТ 520 – 89 и ГОСТ 25347 – 82 определяем отклонения ES, EI, ei, es, строим поля допусков по наружному (D) и внутреннему (d) диаметрам и определяем табличные натяги Nmax и Nmin
Отклонения для внутреннего кольца подшипника:
ES = +8 мкм, EI = -8 мкм
Отклонение для наружного кольца подшипника:
es = +25 мкм, ei = 0 мкм
Определяем поле допуска внутреннего (L5) и наружного (l5) колец [1,табл.
3.9]
L0 = -12 мкм, l0 = -15 мкм
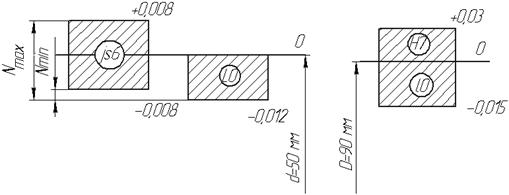
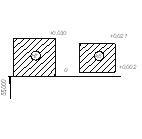
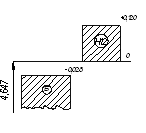
Схема расположения полей допуска
Nmin=dmin- Dmax=ei-ES (2.2)
Nmax=dmax-Dmin=es-EI (2.3)
Nmin=-0,008-(-0,012)=0,004 [мм]
Nmax=0,008-(-0,012)=0,020 [мм]
2.6 Вычислим минимальный допустимый натяг:
 (2.4)
(2.4)
![]() - конструктивный фактор,
- конструктивный фактор,
где d0 – приведенный диаметр внутреннего кольца
![]() (2.5)
(2.5)
![]()
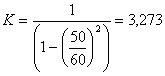
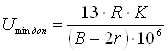 (2.6)
(2.6)
где R – радиальная реакция
![]()
![]() =4 [мкм]
=4 [мкм]
Условие Nmin≥![]() выполняется,
выполняется,
![]()
![]() - условие выполнено
- условие выполнено
2.7 Вычислим максимальный допустимый натяг:
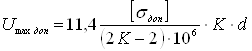 (2.7)
(2.7)
где ![]() – предел прочности шарикоподшипниковой стали
– предел прочности шарикоподшипниковой стали
![]() [мм]
[мм]
![]() - условие выполнено.
- условие выполнено.
![]()
2.8 Проверяем наличие посадочного рабочего зазора:
По внутреннему диаметру (d)определяем min и max радиальный зазор [1,табл. 3.11]:
Gmin=12 мкм, Gmax=29 мкм
Определяем начальный радиальный зазор:
![]() (2.8)
(2.8)
![]() [мкм] или 0,0205 [мм]
[мкм] или 0,0205 [мм]
Определим эффективный натяг:
![]() (2.9)
(2.9)
где ![]() - усреднённый натяг
- усреднённый натяг
![]() (2.10)
(2.10)
![]()
![]()
![]()
![]()
Определим рабочий радиальный зазор:
![]() (2.11)
(2.11)
где ![]()
![]()
![]()
![]()
Условие ![]() - выполнено.
- выполнено.
Определим усилие
запрессовки подшипника на вал (![]() ):
):
![]() (2.12)
(2.12)
Где ![]() - коэффициент трения при запрессовке
- коэффициент трения при запрессовке
![]() - модуль упругости стали
- модуль упругости стали
![]()
![]()
2.9 Определим температуру нагрева подшипника в масле для установки его на вал:
![]() (2.13)
(2.13)
где ![]() - температурный
коэффициент линейного расширения подшипниковой стали
- температурный
коэффициент линейного расширения подшипниковой стали
![]() - сборочный зазор
- сборочный зазор
![]()
![]()
3 Выбор посадок для сопряжений узла и их расчёт
В соответствии с заданием на курсовую работу необходимо назначить посадки для десяти сопряжений сборочной единицы.
Таблица 1 – Выбранные посадки
| Номера сопрягаемых деталей | Наименование сопрягаемых деталей | Выбранные посадки по ГОСТ 25347-82 ( СТ СЭВ144-88) |
| 22 - 04 | Подшипник - вал |
Ç50 |
| 22 – 05 | Подшипник - крышка |
Ç90 |
| 27 - 04 | Шпонка - вал |
Ç55 |
| 04 – 01 | Вал - шестерня |
Ç55 |
| 27 – 01 | Шпонка - шестерня |
Ç55 |
| 16 - 02 | Болт - корпус |
М6 |
| 16 - 08 | Болт - крышка |
Ç6 |
| 08 - 02 | Крышка - корпус |
Ç90 |
| 08 - 21 | Крышка подшипника -манжета |
Ç70 |
| 26 - 04 | Шпонка - вал |
Ç45 |
Расшифровка буквенных обозначений посадок, расчет предельных размеров, зазоров или натягов, построение полей допусков для десяти выбранных сопряжений оформляются в виде таблицы 2.
Таблица 2 – Расчет выбранных посадок
| Номер сопрягаемых деталей | Номинальный размер с отклонениями | Предельные размеры, мм | Схемы полей допусков | |||||
|
Dmax |
Dmin |
dmax |
dmin |
Smax |
Smin |
|||
| 27 - 04 |
Ç55 |
54,968 | 54,894 | 55,000 | 54,926 | 0,042 | 0,106 |
|
| 26 - 04 |
Ç45 |
44,974 | 44,912 | 45,000 | 44,938 | 0,036 | 0,088 |
|
| 22 - 04 |
Ç50 |
50 | 49,988 | 50,008 | 49,992 | 0,008 | 0,02 |
|
| 22 – 05 |
Ç90 |
90,035 | 90,000 | 90,000 | 89,985 | 0,05 | 0 |
|
| 04 – 01 |
Ç55 |
55,030 | 55,000 | 55,021 | 55,002 | 0,028 | 0,021 |
|
| 27 – 01 |
Ç55 |
55,037 | 54,963 | 55,000 | 54,926 | 0,111 | 0,037 |
|
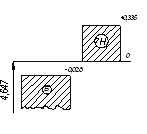
| 08 - 02 |
Ç90 |
90,011 | 89,989 | 89,880 | 89,660 | 0,351 | -0,109 |
|
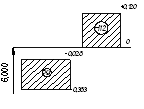
| 08 - 21 |
Ç70 |
70,046 | 70 | 70 | 69,926 | 0,120 | 0 |
|
| 16 - 02 |
Ç6 |
–– | 6,00 | 5,972 | 5,637 | –– | 0,028 |
|
|
Ç5,188 |
5,388 | 5,188 | 5,160 | 4,976 | 0,413 | 0,028 |
|
|
|
Ç4,647 |
4,982 | 46,47 | 4,619 | –– | –– | 0,028 |
|
|
| 16 - 08 |
Ç6 |
6,120 | 6,000 | 5,072 | 5,637 | 0,483 | 0,028 |
|
|
Ç5,188 |
5,308 | 5,188 | 5,160 | 4,975 | 0,333 | 0,028 |
|
|
|
Ç4,647 |
4,767 | 4,647 | 4,619 | –– | –– | 0,028 |
|
|
4 Выбор средств измерений деталей
Выбор измерительных средств осуществляется с учётом допустимой погрешности измерений, а также погрешности измерительных средств. Значение допустимой погрешности измерения δизм зависит от величины допуска на изготовление изделия IT, который, в свою очередь связан с номинальным размером и квалитетом. Для размеров от 1 до 500 ГОСТ 8051-81 устанавливает 15 рядов наибольших допустимых погрешностей измерения в зависимости от величины допуска .
При выборе средств и методов измерения необходимо подобрать такое средство (инструмент, прибор), предельная погрешность которого была бы ближе к допустимой погрешности измерения размера (δизм) и не превышала бы эту величину. Для выбранного средства измерения по справочным данным [5] следует установить его основные характеристики: пределы измерения, цену деления.
Результаты выбора измерительных средств оформляются в виде таблицы 3.
| Номера сопрягаемых деталей |
|
Средства измерения | Цена деления | Пределы измерения |
| 22 - 04 |
0,074 0,074 |
Нутромер индикаторный (ГОСТ 868-72) Микрометр гладкий (ГОСТ 6507-78) |
0,01 0,01 |
50 - 120 50 - 80 |
| 22 - 05 |
0,035 0,015 |
Нутромер индикаторный (ГОСТ 868-72) Микрометр гладкий (ГОСТ 6507-78) |
0,01 0,01 |
50 - 120 80 - 120 |
| 27 - 04 |
0,074 0,074 |
Микрометр гладкий (ГОСТ 6507-78) Нутромер индикаторный (ГОСТ 868-72) |
0,01 0,01 |
50 - 80 50 - 120 |
| 04 - 01 |
0,030 0,019 |
Микрометр гладкий (ГОСТ 6507-78) Нутромер индикаторный (ГОСТ 868-72) |
0,01 0,01 |
50 - 80 50 - 120 |
| 27 - 01 |
0,074 0,074 |
Микрометр гладкий (ГОСТ 6507-78) Нутромер индикаторный (ГОСТ 868-72) |
0,01 0,01 |
0 - 25 50 - 120 |
| 26 - 04 |
0,062 0,062 |
Микрометр гладкий (ГОСТ 6507-78) Нутромер индикаторный (ГОСТ 868-72) |
0,01 0,01 |
0 - 25 1 - 18 |
| 08 - 21 |
0,046 0,074 |
ГОСТ 23360-78 Нутромер индикаторный (ГОСТ 868-72) |
0,01 | 50 - 120 |
| 08 - 02 |
0,022 0,440 |
Микрометр гладкий (ГОСТ 6507-78) Нутромер индикаторный (ГОСТ 868-72) |
0,01 0,01 |
80 - 120 50 - 120 |
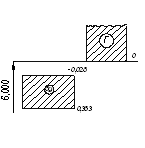
| 16 - 02 |
0,200 0,185 |
Микроскоп инструментальный ММИ и БМИ (ГОСТ 2094-71) Нутромер индикаторный (ГОСТ 868-72) |
0,005-0,01 0,01 |
3 - 6 1 - 18 |
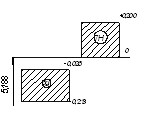
| 16 - 08 |
0,120 0,335 |
Микроскоп инструментальный ММИ и БМИ (ГОСТ 2094-71) Нутромер индикаторный (ГОСТ 868-72) |
0,005-0,01 0,01 |
3 - 6 1 - 18 |
5 Расчет рабочих и контрольных калибров
5.1 Выбираем сопряжение:
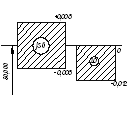
корпус – вал Æ![]()
Стоим поля допусков для данного сопряжения
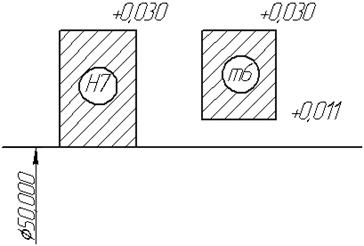
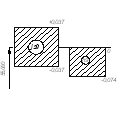
Рис.1 - Схема полей допуска сопряжения.
5.2 Размечаем нулевые линии для построения полей допусков калибров:
- Калибр – пробка (для контроля отверстий):
Проходная сторона (наименьшее отверстие):
Dmin=Dн+EI (5.1)
Dmin=Dн+EI=50+0=50 [мм]
Непроходная сторона (наибольшее отверстие):
Dmax=Dн+ES (5.2)
Dmax=Dн+ES=50+0,030=50,03 [мм]
- Калибр – скоба (для контроля вала):
Проходная сторона (наименьший вал):
dmin=dн+ei (5.3)
dmin=dн+ei=50+0,011=50,011 [мм]
Непроходная сторона (наибольший вал):
dmax=dн+es (5.4)
dmax=dн+es=50+0,03=50,03 [мм]
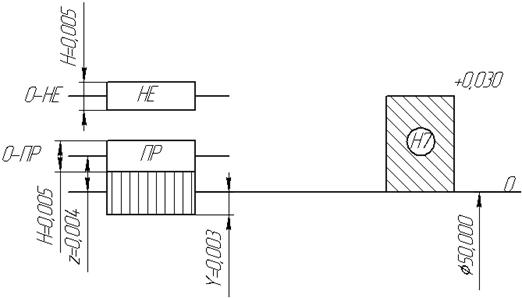
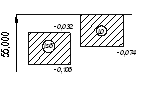
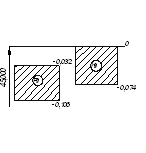
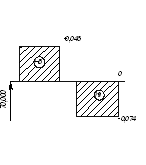
Рисунок 2 – Схема расположения поля допуска отверстия и полей допусков калибров
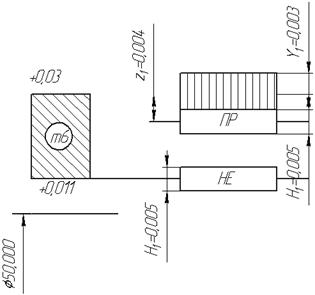
Рисунок 3 – Схема расположения поля допуска вала и полей допусков калибров
5.3 По таблицам допусков на калибры (ГОСТ 24853-81) берем отклонения:
- Для пробок Z=4 мкм, Y=3 мкм, H=Hs=5,0 мкм
- Для скоб Z=4 мкм, Y=3 мкм, H1=Hs=5,0 мкм
Поля допусков калибров строятся от соответствующих нулевых линий.
Участок износа штрихуется вертикальными линиями.
5.4 Рассчитываем предельные размеры калибров, результаты оформляем в виде таблицы 4.
Для калибра пробок:
![]() мм
мм
![]() мм
мм
![]() мм
мм
![]() мм
мм
![]() мм
мм
Для калибра скоб:
![]() мм
мм
![]() мм
мм
![]() мм
мм
![]() мм
мм
![]() мм
мм
Таблица 4 – Предельные размеры калибров
| Размеры, мм | Для пробок | Для скоб |
| Проходная сторона | ||
| Наибольший | 50,0065 | 50,0285 |
| Наименьший | 50,0015 | 50,0235 |
| Изношенный | 49,997 | 50,033 |
| Непроходная сторона | ||
| Наибольший | 50,0325 | 50,0135 |
| Наименьший | 50,0275 | 50,0085 |
5.5 Определяем исполнительные размеры калибров для простановки их на чертежах:
Пробки Р – ПР 50,0065-0,005 Р – НЕ 50,0325-0,005
Скобы Р – ПР 50,0235+0,005 Р – НЕ 50,0085+0,011
6 Расчёт и выбор посадки с натягом
Исходные данные:
Номинальный диаметр сопряжения D=140 мм;
Наружный диаметр втулки D2=240 мм;
Длина сопряжения L=80 мм;
Передаваемый крутящий момент Mкр=10000 Н·м;
Материал втулки и вала сталь 50;
Диаметр осевого отверстия D1=0 мм; осевое усилие P=0.
Шероховатость поверхности втулки RzD=6,3 мкм, Rzd=3,2 мкм
6.1 Определяем величину удельного контакта эксплуатационного Pз между поверхностями сопряжения вала и втулки:
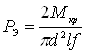 (6.1)
(6.1)
где d – номинальный диаметр сопряжения, ![]() – длина сопряжения,
– длина сопряжения,![]() - коэффициент трения при
запрессовке.
- коэффициент трения при
запрессовке.
![]() [Па]
[Па]
6.2 По графику деформаций [1, рис. 2.1] и величинам Pэ/sт; d1/d2 и d/d2 определяем характер деформирования отверстия и вала, вызванный удельным давлением:
![]() (6.2)
(6.2)
По графику [1, рис. 2.1], учитывая отношения (5.2), делаем вывод что характер деформирования отверстия и вала - упругий.
6.3 По графику деформаций
[1, рис. 2.1] определяем наибольшее допустимое значение ![]() на границе допустимой зоны
деформирования (кривая «а» или «б») и рассчитываем значение
на границе допустимой зоны
деформирования (кривая «а» или «б») и рассчитываем значение ![]() :
:
Наибольшее допустимое
значение ![]() - кривая «а».
- кривая «а».
По графику [1, рис. 2.1]
определяем, что ![]() .
.
![]() [Па] – предел текучести материала.
[Па] – предел текучести материала.
![]() [Па]
[Па]
![]() [мм]
[мм]
6.4 По графику [1, рис. 2.1] находим значение коэффициента неравномерности распределения удельного давления æ, затем рассчитываем наибольшее (для этого коэффициента) значение удельного давления Pнб доп:
æ=0,8
PНБ ДОП = PНБ· æ (6.3)
PНБ ДОП =0,88·108·0,8=7,04·107 [Па]
6.5 Определяем коэффициенты формы отверстия и вала:
CA = 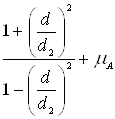 (6.4)
(6.4)
CВ =  (6.5)
(6.5)
где ![]() -
коэффициент Пуассона [1, табл. 2.2].
-
коэффициент Пуассона [1, табл. 2.2].
CA = 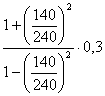 =0,6
=0,6
CВ = 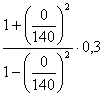 =0,3
=0,3
6.6 Рассчитываем величину натягов:
Nmin = Рэ 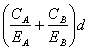 (6.6)
(6.6)
где EA=EB=2·1011 Па – модуль упругости стали.
Nmin = 5,1·107 ![]() [мм]
[мм]
Nmax = Pнб.доп 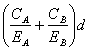 (6.7)
(6.7)
Nmax = 7,04·107![]() =0,044 [мм] или 44 [мкм]
=0,044 [мм] или 44 [мкм]
6.7 Рассчитываем поправку на смятие микронеровностей сопрягаемых поверхностей и находим расчетные величины натягов для выбора посадки:
![]() (6.8)
(6.8)
где К1 и К2 коэффициенты, учитывающие поправку на смятие микронеровностей.
Определяем по таблице [1, табл. 2.4]коэффициенты K1 и K2:
K1=K2=0,25
![]() [мкм] или 0,004 [мм]
[мкм] или 0,004 [мм]
Nminр = Nmin + ΔШ (6.9)
Nminр = 0,032 + 0,004=0,036 [мм]
Nmaxр = Nmax + ΔШ (6.10)
Nmaxр = 0,044 + 0,004=0,048 [мм]
6.8 Проверяем выполнение условий и выбираем стандартную посадку:
Nmaxр![]() Nmax – условие выполнено
Nmax – условие выполнено
0,048 мм>0,004 мм
Nminр![]() Nmin – условие выполнено
Nmin – условие выполнено
0,036 мм>0,032 мм
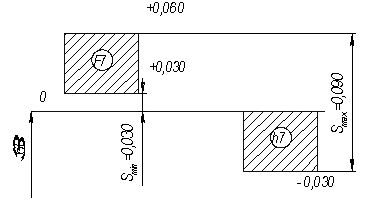
Выбираем стандартную посадку по ГОСТ 25347 – 82 и строим её поля допусков с указанием размеров, натягов и отклонений в системе отверстий
![]() мкм
мкм ![]() мкм,
мкм,
![]() .
.
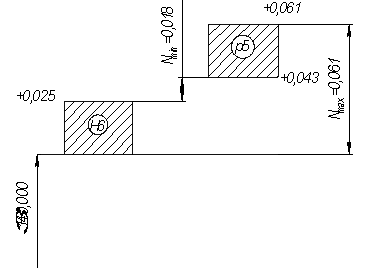
Рисунок 4 – Схема расположения поля допуска посадки с натягом.
6.9 Определяем наибольшее удельное давление на сопрягаемых поверхностях при наибольшем натяге выбранной посадки
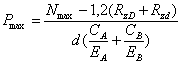 (6.11)
(6.11)
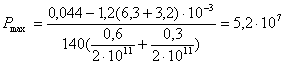 [Па]
[Па]
6.10 Вычисляем наибольшее напряжение во втулке:
σд = 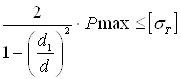 (6.12)
(6.12)
где sД – наибольшее напряжение во втулке.
σд = 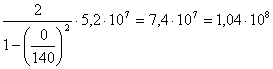 [Па]
[Па]
6.11 Проверяем прочность втулки по выполнению неравенства:
σд![]()
![]() - условие выполнено
- условие выполнено
1,04·108 Па<2,94·108 Па
7 Расчёт точности зубчатой передачи
Исходные данные:
- число витков червяка z1=2;
- число зубьев червячного колеса z2=50;
- окружная скорость колёс
![]() , м/с;
, м/с;
- модуль зубчатой передачи m=5, мм;
- рабочие температуры колёс и корпуса t1=60˚C и t2=25˚C;
- материал колёс: СИЛУМИН; корпуса: СИЛУМИН;
- вид передачи: ДЕЛИТЕЛЬНЫЕ МЕХАНИЗМЫ.
7.1 По величине окружной
скорости ![]() м/с выбираются степени
точности зубчатой передачи [1.табл.5.1]
м/с выбираются степени
точности зубчатой передачи [1.табл.5.1]
8 - степень точности по нормам плавности.
Т.к. для скоростных передач норма контакта принимается на одну степень ниже, то:
9- степень точности по нормам контакта.
8 - 8 – 9
7.2 Определяется межосевое расстояние
![]() мм
мм
7.3 Определяется температурная компенсация зазора
![]() (7.1)
(7.1)
где ![]() температурные коэффициенты
линейного расширения материала втулки и вала[табл.1.2]; α=20˚C –угол зацепления,
град;
температурные коэффициенты
линейного расширения материала втулки и вала[табл.1.2]; α=20˚C –угол зацепления,
град;
![]() мм =68мкм
мм =68мкм
7.4 Оптимальная толщина слоя смазки jn2.
jn2 = 10·m=10·5=50 мкм – для делительных передач;
7.5 Определяется минимальный боковой зазор передачи
jnmin ![]() мкм
мкм
7.6 По таблицам ГОСТ 1643-81[5.10] подбирается вид сопряжения:«В»
8 - 8 - 9В
7.7 Выбор контролируемых параметров и средств их измерения.
Стандарт на допуски зубчатых колёс и передач (ГОСТ 1643-81) предусматривает для каждой нормы точности ряд показателей. Однако на основании многолетнего опыта работы каждый вид машиностроения разрабатывает свои рекомендации по выбору комплексов контролируемых параметров. Для химического и пищевого машиностроения эти рекомендации приведены в работе , по которой и следует подбирать комплексы для контроля зубчатых колёс. Измерительные средства для контроля каждого комплекса выбираются с учётом степени точности и основных характеристик колёс по справочным данным. В пояснительной записке должны быть приведены основные метрологические характеристики измерительных средств (цена деления, пределы измерения и т.д.).
| Степень точности | норма | Контролируемый параметр | Наименование средств измерений, модель |
Цена деления |
Предел измерения |
| 8 | кинема-тическая точность |
радиальное биение
Колебании длинны общей нормали
|
Биеметр Б=10м Нормометр БВ-504-6-26 |
0,001 0,02 |
m=1,0 d=20 |
| 8 |
плавность работы |
Угловое отклонение шага
|
шагомер для основного и окружного шага ШМ-1 | 0,001 |
m d=50 |
| 9 |
контакта зубьев |
Суммарное пятно контакта % по высоте не менее 20 не менее 20 по длине не менее 25 не менее 25 |
контактно-обкаточное приспособление универсальное 5710 | –– | d<120 |
| В |
бокового зазора |
Отклонение средне длинны общей нормали
Допуск на среднюю длину
|
Штангензубомер | 0,02 |
0 |
8 Расчёт и выбор посадки с зазором
Исходные данные:
Номинальный диаметр сопряжения d=60 мм;
Длина сопряжения l=40 мм;
Угловая скорость вращения n=1000 об/мин;
Нагрузка на опору R=2 Кн;
Марка смазочного масла: индустриальное 20
Шероховатость поверхности втулки RzD=4 мкм; вала Rzd=2 мкм
Материал втулки – чугун, вала – сталь 50.
8.1 Рассчитываем угловую скорость:
![]() (8.1)
(8.1)
где n – угловая скорость вращения
![]() [рад/с]
[рад/с]
8.2 Определяем среднее удельное давление:
![]() (8.2)
(8.2)
где R – нагрузка на опору
![]() [Н/м2]
[Н/м2]
8.3 Устанавливаем допустимую минимальную толщину маслянистого слоя – h:
![]() (8.3)
(8.3)
где RzD и Rzd – соответственно шероховатость втулки и вала.
![]() [мм]
[мм]
8.4 В соответствии с заданием определяем вязкость масла [1,табл. 1.3]:
![]() [Па·с]
[Па·с]
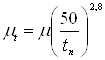 (8.4)
(8.4)
где tп=500С – температура нагрева подшипника в масле
![]() [Па·с]
[Па·с]
8.5 Определяем функциональный комплекс:
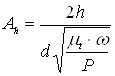 (8.5)
(8.5)
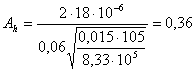
8.6 По графику [1, рис. 1.1] определяем относительные эксцентриситеты:
![]() и
и ![]()
8.7 Рассчитываем минимальный допустимый зазор:
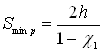 (8.6)
(8.6)
где ![]() - относительный
эксцентриситет при Smin.
- относительный
эксцентриситет при Smin.
![]() [м]
[м]
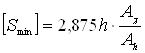 (8.7)
(8.7)
![]() [м],
[м],
где ![]() вычисляется по таблице [1,
табл. 1.6] в зависимости от эксцентриситета и отношения l/d.
вычисляется по таблице [1,
табл. 1.6] в зависимости от эксцентриситета и отношения l/d.
8.8 Определяем температурное изменение зазора:
![]() (8.8)
(8.8)
Где a1 и a2 соответственно коэффициент линейного расширения материала вала и втулки
![]() [м]
[м]
8.9 Рассчитываем минимальный действующий зазор:
![]() (8.9)
(8.9)
![]() [м]
[м]
8.10 Рассчитываем максимальный допустимый зазор:
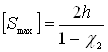 (8.10)
(8.10)
Где ![]() - относительный
эксцентриситет при Smax.
- относительный
эксцентриситет при Smax.
![]() [м]
[м]
8.11 Рассчитываем максимальный действующий зазор:
![]() (8.11)
(8.11)
![]() [м]
[м]
![]() [мм] и
[мм] и ![]() [мм]
[мм]
По таблицам ГОСТ 25347 82 (СТСЭВ 144-88) выбираем предельные зазоры в системе отверстия:
![]() мкм,
мкм, ![]() мкм,
мкм,
![]()
9 Расчёт размерной цепи вероятностным методом
Расчет размерной цеп вероятностным методом позволяет установить на составляющие звенья более широкие допуски, чем те, получаются при решении задачи методом полной взаимозаменяемости
В основе этого метода служит теорема математической статистики, устанавливающие свойства дисперсии. Замыкающее звено размерной цепи принимается за случайную величину, являющейся суммой неизвестных случайных величин, т.е. суммой независимых составляющих звеньев цепи.
Как известно из теории вероятности, при любых законах распределение случайных погрешностей отдельных составляющих звеньев погрешность замыкающего звена также будет случайной погрешностью , получающейся по определенному закону распределения.
Распределения размерах в пределах допуска может проходить по одному из следующих законов:
а. нормального распределения
б. равнобедренного треугольника(Симпсона)
в. равной вероятности
В результате влияния систематических и случайных центр группирования размеров может не совпадать с серединой поля допуска, а зона рассеивания с величиной поля допуска.
Дано:
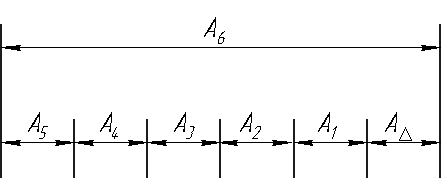
А1 А2 А3 А4 А5 АΔ А6
45 100 30 128 45 ![]() 400
400
Н Н РТ Н Н РТ
Возможный брак: А1=1%; А3=2%.
Выполнение расчета
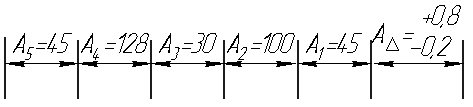
9.1 Номинальный размер замыкающего звена АΔ, мм, рассчитываем по формуле
АΔ= А6-( А1+ А1+А3+А4+А5 ), (9.1)
АΔ=400-(45+100+30+128+45)=52мм
9.2 Расчет средний точности размерной цепи
Введем следующие коэффициенты
![]() - коэффициент относительного
рассеивания, который равен для: нормального распределения 0,333; для закона
равнобедренного треугольника 0,408.
- коэффициент относительного
рассеивания, который равен для: нормального распределения 0,333; для закона
равнобедренного треугольника 0,408.
9.3 В зависимости от
процента брака определяем для каждого звена добавочный множитель ![]() :
:
А1: 1% - 2,57
А2: 0,27% - 3,00
А3: 2% - 2,32
А4: 0,27% - 3,00
А5: 0,27% - 3,00
А6: 0,27% - 3,00
9.4 Определяют произведение i∙t·λi. Возводят это произведение в квадрат, где i- единица допуска, выбирается в зависимости от номинальных размеров по ГОСТ 23347-82
А1 А2 А3 А4 А5 А6
45 100 30 128 45 400
1,56 2,17 1,31 2,52 1,56 3,54
Суммируют все значения величин (i·t·λi)2 и определяют значение среднего коэффициента точности цепи – аср по формуле:
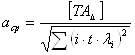
где [![]() ] - заданное значение допуска, имеем
] - заданное значение допуска, имеем
![]() мм=1000мкм
мм=1000мкм
Таблица 5 – Расчёт средней точности размерной цепи
|
Аi ном |
i | t |
λi |
(i · t ·λi)2 |
|
|
А1 =45 А2 =100 А3 =30 А4 =128 А5 =45 А6 =400 |
1,56 2,17 1,31 2,52 1,56 3,54 |
2,57 3,00 2,32 3,00 3,00 3,00 |
0,333 0,333 0,408 0,333 0,333 0,408 |
1,782 4,700 1,538 6,335 2,427 18,775 |
5,963 |
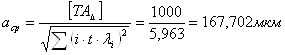
По полученному коэффициенту из табл. 1.2 выбирают ближайший более точный квалитет допусков звеньев размерной цепи [1].
Принимаем ![]() ,
соответствует 12 квалитету.
,
соответствует 12 квалитету.
9.5. Определение вероятностного допуска замыкающего звена. По табл. 1.3.[1] определяют допуски соответствующих звеньев размерной цепи.
Таблица 6 – Расчёт вероятностного допуска замыкающего звена
|
Аi ном |
TAi |
λi |
t |
(TAi · λi · t)2 |
|
|
А1 =45 А2 =100 А3 =30 А4 =128 А5 =45 А6 =400 |
250 350 210 400 250 570 |
0,333 0,333 0,408 0,333 0,333 0,408 |
2,57 3,00 2,32 3,00 3,00 3,00 |
45775,672 122255,123 39512,534 159680,160 62375,063 486757,382 |
957,265 |
Вычисляем вероятностный допуск замыкающего звена по формуле:
![]() =
=![]() мкм
мкм
Условие ТАΔ ≤ [ТАΔ] выполняться , т.к.
957,265<1000
9.6 Полученные допуски составляющих звеньев разбивают на отклонения, пользуясь следующими правилами:
а) если среднее отклонение звена Em(АΔ) = ![]() равно нулю, то отклонения для всех
звеньев принимаются симметричными, т.е.
равно нулю, то отклонения для всех
звеньев принимаются симметричными, т.е. ![]() ТАi;
ТАi;
б) если Em(АΔ) = ![]() положительно, то отклонения
принимаются:
положительно, то отклонения
принимаются:
для увеличивающих звеньев ES(Ai) = + TAi; EI(Ai) = 0;
для уменьшающих звеньев ES(Ai) = 0; EI(Ai) = − TAi.
в) если Em(АΔ) = ![]() отрицательно, то отклонения
принимаются:
отрицательно, то отклонения
принимаются:
для увеличивающих звеньев ES(Ai)=0; EI(Ai)=−TAi;
для уменьшающих звеньев ES(Ai)=+TAi; EI(Ai)= −TAi.
Звено А6 - увеличивающаяся,
звено А1 - А5 - уменьшающиеся.
Em(АΔ) = ![]() мм=300мкм>0,
мм=300мкм>0,
Отклонения принимаются:
А1 : ES(45)=0 мкм; EI(45)=-250 мкм;
А2 : ES(100)=0 мкм; EI(100)=-350 мкм;
А3 : ES(30)=0 мкм; EI(30)=-210 мкм;
А4 : ES(128)=0 мкм; EI(128)=-400 мкм;
А5 : ES(45)=0 мкм; EI(45)=-250 мкм;
А6 : ES(400)=+570мкм; EI(400)=0 мкм;
Для увеличивающегося звена Ç400h12(![]() )
)
Для уменьшающихcя звеньев Ç45H12(![]() ); Ç100H12(
); Ç100H12(![]() ); Ç30H12(
); Ç30H12(![]() ); Ç128H12(
); Ç128H12(![]() );Ç45H12(
);Ç45H12(![]() );
);
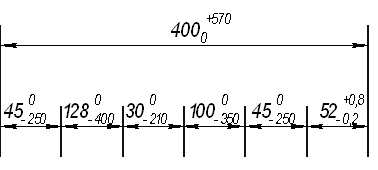
Т.к. разбивка отклонений произвольна, то обязательное условие
![]()
может не выполняться.
![]()
![]() - условие не выполняется,
- условие не выполняется,
тогда принимаем звено А2 в качестве зависимого:
![]()
![]()
![]() .
.
Отклонения зависимого звена находят по правилу:
ES(Азав) = Em(Азав) + ½Тзав;
EI(Азав) = Em(Азав) - ½Тзав.
ES(Азав)![]() мкм
мкм
EI(Азав)![]() мкм
мкм
9.7 Процент годных деталей при сборке размерной цепи вычисляют в следующей последовательности:
а) определяют среднее квадратичное отклонение звена АΔ:
σ = ![]() =
=![]() ;
;
б) находят границы нового допуска
X =![]() =
=![]() мкм;
мкм;
в) находят пределы интегрирования расчётного вероятностного допуска
Z = ![]() =
=![]() ;
;
г) рассчитывают вероятность изготовления годных деталей по формуле
Р = 2Ф(Z);
где Ф(Z) - значение функции Лапласа
Ф(2,87)=0,4979;
Р = ![]()
д) процент годных деталей
П = Р∙100%;
![]()
е) брак Б :
Б= 100% - П=100%-99,59%=0,41%.
Список используемых стандартов
ГОСТ 2.307-68 ЕСКД. Нанесение размеров и предельных отклонений.
ГОСТ 2.308-79 ЕСКД. Указание на чертежах допусков формы и расположения поверхностей.
ГОСТ 2.309-73 ЕСКД. Обозначение шероховатости поверхностей.
ГОСТ 25346-89 ЕСДП. Основные нормы взаимозаменяемости. Общие положения, ряды допусков и основных отклонений.
ГОСТ 25347-89 ЕСДП. Поля допусков и рекомендуемые посадки.
ГОСТ 6636-69 Основные нормы взаимозаменяемости. Нормальные линейные размеры.
ГОСТ 27284-87 Калибры. Термины и определения.
ГОСТ 11708-82 Основные нормы взаимозаменяемости. Резьба. Термины и определения.
ГОСТ 3478-79 Подшипники качения. Основные размеры.
ГОСТ 3325-85 Подшипники качения. Поля допусков и технические требования к посадочным поверхностям валов и корпусов. Посадки.
ГОСТ 1643-81 Основные нормы взаимозаменяемости. Передачи зубчатые цилиндрические. Допуски.
ГОСТ25142-82 Шероховатость поверхности. Термины и определения.
ГОСТ 16319-80 Цепи размерные. Термины и определения. Методы расчёта.
© 2009 База Рефератов