Реферат: Конические сечения

Реферат: Конические сечения

Министерство образования РФ

Калужский государственный педагогический университет

Им. К.Э. Циолковского

Реферат

«Конические сечения»

Калуга

Содержание:

1.    Работы Аполлония

2.    «Конические сечения» Аполлония.

2.1 Вывод уравнения кривой для сечения прямоугольного конуса вращения

2.2 Вывод уравнения для параболы

2.3 Вывод уравнения для эллипса и гиперболы

2.4 Инвариантность конических сечений

2.5 Дальнейшее исследование конических сечений в трудах Аполлония

2.6 Дальнейшее развитие теории конических сечений

3.    Заключение

4.    Список литературы

Работы Аполлония

Аполлоний родился в Пергах в Малой Азии. Расцвет его деятельности падает примерно на 210г. до н.э. В это время он жил в Александрии, куда переехал еще юношей и где учился под руководством математиков школы Евклида. Аполлоний прославился как геометр и астроном. Умер он около 170г. до н. э.

В математике Аполлоний более всего известен своими «Коническими сечениями», в которых он дал полное изложение теории, причем развил аналитические и проективные методы. Аполлоний написал трактат «О вставках», посвященный классификации задач которые решаются с помощью вставок. Такие задачи могут оказаться разрешимыми циркулем и линейкой (плоские задачи), с помощью конических сечений (телесные задачи) и с помощью других кривых (линейные). Выявление того, к какому классу относится та или иная задача, могло означать начало их алгебраической классификации. Интерес Аполлония к алгебраическим проблемам проявился и в другой его работе – «О неупорядоченных иррациональностях», в которой он продолжал классификацию Евклида.

Чисто геометрическими работами Аполлония являются: работа «О спиральных линиях», в которой он рассматривает спирали на поверхности цилиндра, «О касании», где разбирается знаменитая задача Аполлония: «Даны три вещи, каждая из которых может быть точкой, прямой или окружностью; требуется провести окружность, которая проходила бы через каждую из данных точек и касалась бы каждой из данных прямых или окружностей».

Из сочинений «О плоских геометрических местах» можно заключить, что Аполлоний рассмотрел преобразование плоскости на себя, которые переводят прямые и окружности в прямые и окружности. Частным случаем этих преобразований являются преобразования подобия и инверсии некоторой точки.

Некоторые труды Аполлония были утрачены и не дошли до наших дней.

«Конические сечения» Аполлония

«Конические сечения» состоят из восьми книг. Первые четыре, в которых, по словам автора, излагаются элементы теории, дошли до нас по-гречески, следующие три – в арабском переводе Сабита ибн Корры, последняя – восьмая книга - утеряна. Имеется реконструкция ее текста, принадлежащая английскому астроному Э. Галлею (XVIII в.).

Кривые второго порядка были впервые рассмотрены в связи с задачей удвоения куба, Менехм представил их как плоские сечения прямоугольного, тупоугольного и остроугольного конусов вращения. Такое стереометрическое представление гарантировало существование и непрерывность рассматриваемых кривых. Затем Менехм переходил к выводу основного планиметрического свойства сечения, которое древние называли симптомом (уравнение кривой).

Вывод уравнения кривой для сечения прямоугольного конуса вращения

Пусть OAB – сечение этого конуса плоскостью, проходящей через ось OL, и пусть PLK – след плоскости, перпендикулярной к образующей этого конуса (рис. 1). Тогда KM2 = AK•KB, так как AMB – полукруг. Но AK=PP′=√2LP2, а KB=√2KP2, поэтому KM2=2LP•KP.

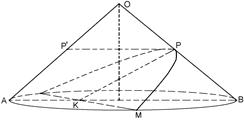
Рис. 1

Обозначим KM через y, KP – через p, тогда получим

y2=2px. (1)

Это уравнение, или симптом, кривой, которое записывается с помощью буквенной символики, а древние записывали в словесно – геометрической форме: квадрат на полухорде KM в каждой точке равен прямоугольнику PKSR, построенному на отрезке PK оси до вершины (x) и на постоянном отрезке PR (рис. 2).

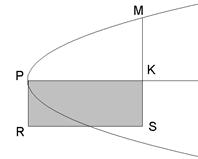
Рис. 2

Аналогично выводилось уравнение для сечений остроугольного и тупоугольного конусов, т.е. эллипса и гиперболы:

 = и =,   (2)

где 2a – большая ось эллипса или действительная ось гиперболы,

а р –постоянная.

В случае, когда р=а, уравнения (2) принимают вид

y2=x(2a-x) и y2=x(2a+x)    (3)

первое из которых является уравнением окружности радиуса а, а второе – уравнением равносторонней гиперболы. Эллипс и гипербола (2) могут быть получены из окружности и гиперболы (3) сжатием к оси абсцисс в отношении √p/a.

Аполлоний прежде всего дает более общее определение. Во – первых, он берет произвольный круговой конус; во – вторых, рассматривает обе его полости ( что дает ему возможность изучать обе ветки гиперболы); наконец, он проводит сечение плоскостью расположенной под любым углом к образующей.

На привычном языке аналитической геометрии, можно сказать, что до Аполлония конические сечения рассматривались по отношению к прямоугольной системе координат, причем одна из осей совпадала с главным диаметром, а вторая проходила перпендикулярно к ней через вершину кривой; Аполлоний же относил кривые к любому диаметру касательной проведенной в одном из его концов, т.е. к некоторой косоугольной системе координат.

После стереометрического определения Аполлоний также дает вывод симптомов – уравнений кривых. При этом он классифицирует полученные кривые по виду определяющего их уравнения, т.е. в основу кладется точка зрения, свойственная аналитической геометрии.

Вывод уравнения для параболы

Пусть BAC – сечение кругового конус плоскостью, проходящей через ось (рис. 3), и пусть проведена плоскость GHD так, что DE перпендикулярна BC, а GH параллельна AB ( GH можно было выбрать параллельной AC). Найдем уравнение кривой DGE, полученной в сечении.

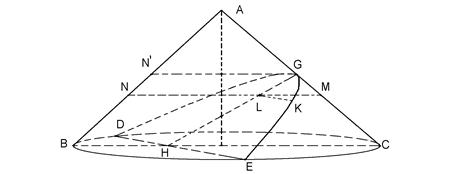
Рис. 3

Пусть К – произвольная точка этой кривой. Проведем KL параллельно DE и MN параллельно BC. Плоскость проходящая через KL и MN, будет параллельна плоскости основания и, как это ранее доказал Аполлоний, будет пересекать конус по кругу. Поэтому KL2=ML•LN.

Но , т.е. ,

, т.е. .

Значит,

Отрезок GL есть переменное расстояние проекции точки Д от вершины, члены  постоянны. Аполлоний выбирает такой отрезок GF, что

Тогда KL2=GF•LG. Это и есть симптом – уравнение сечения.

Если обозначить KL=y, LG=x, GF=2p, то мы получим уравнение в привычной форме: y2=2px.

У Аполлония уравнение записывается также словесно – гречески: если GH – один из диаметров параболы, а KL – полухорда, сопряженная с этим диаметром, то Аполлоний откладывает GR = 2р перпендикулярно к GH. Тогда утверждается, что в каждой точке квадрат, построенный на LK (рис. 4), должен равняться прямоугольнику GRSL, т.е. GL•GR.

Название «парабола» происходит от названия Аполлония παραβολή (приложение), так как задача о построении точки этой кривой сводится к задаче о приложении (до Аполлония параболу называли сечением прямоугольного конуса вращения).

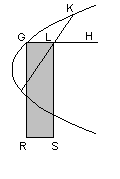
Рис. 4

Вывод уравнения для эллипса и гиперболы

Аналогично Аполлоний получает уравнение эллипса и гиперболы.

Так, для эллипса доказывается, что LK2= пл. GLL′G′ (рис. 5), где GH=2a – некоторый диаметр эллипса, LK – полухорда, сопряженная с ним, GR=2p – постоянная, причем GR перпендикулярна GH. Чтобы перейти к более привычной форме записи, заметим, что

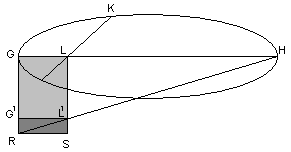Рис. 5

,

т.е.

,

или

.

Таким образом, задача о построении точек эллипса сводится к задаче о приложении с недостатком («эллиптическая задача»), чем и объясняется название «эллипс» ( έλλειψις недостаток). Это название было введено Аполлонием, до него эллипс называли сечением остроугольного конуса вращения.

Аналогично для гиперболы (рис. 6) получается уравнение

LK2= пл. GLL′G′, т.е. , или .

Следовательно, задача о построении точек гиперболы сводится к задаче о приложении с избытком («гиперболическая задача»), чем и объясняется название «гипербола» ( ύπερβολή избыток). Это название также было введено Аполлонием, до него гиперболу называли сечением тупоугольного конуса вращения.

Построенный отрезок GR=2p, откладываемый перпендикулярно диаметру GH, Аполлоний назвал «прямой стороной».

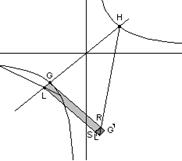
Рис. 6

В настоящее время величину p именуют параметром канонического сечения (в случае эллипса и гиперболы с полуосями a и b p=b2/a, и коэффициент сжатия √p/a, преобразующего окружность или равностороннюю гиперболу в данный эллипс или гиперболу, равен b/a).

Классификация конических сечений у Аполлония была по существу, алгебраической.

Инвариантность конических сечений

Аполлоний прекрасно понимал (и это сближало его с геометрами Нового времени), что такая классификация законна только в том случае, если вид уравнения не изменяется при отнесении кривой к другому ее диаметру и сопряженным с ним хордам.

В первой книге он исследует данный вопрос. Для этого необходимо было определить направление хорд, сопряженных с любым диаметром. При стереометрическом определении сопряженные направления получаются автоматически. Однако для решения задачи, поставленной Аполлонием, нужно определение, независимое от стереометрии. Аполлоний и делает это: он доказывает, что прямая проведенная через точку A канонического сечения параллельно направлению хорд, сопряженных с диаметром, проходящим через A, есть касательная. После этого он строит касательную к параболе, эллипсу, кругу и гиперболе.

Пусть P – некоторая точка на параболе и АА′ один из диаметров (рис. 7). Аполлоний доказывает, что касательная PR отсечет от продолжения диаметра отрезок AR=AQ, если PL хорда, сопряженная с AA′. Для гиперболы, эллипса и круга он получает соотношение  (рис. 8, для эллипса)

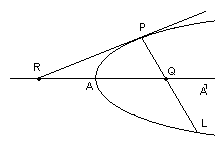
Рис. 7

RA:RA′=QA:QA′.

Аполлоний преобразует затем уравнение эллипса и гиперболы так, что начало координат оказывается в центре кривой, а уравнение параболы так, что начало координат совмещается с вершиной этой кривой.

Таким образом, здесь осями координат служат два сопряженных диаметра. После этого он показывает, что вид уравнения не изменяется, если в качестве новых осей взять любой из диаметров кривой и касательную, проведенную в одном из его концов.

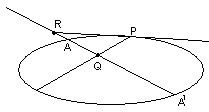
Рис. 8

В первой книги Аполлоний рассматривает множество систем координат, зависящее от одного параметра, так как эти системы координат определяются одной точкой кривой – концом диаметра, и доказывает инвариантность уравнений эллипса, гиперболы и параболы относительно преобразований соответствующих систем координат.

В конце первой книги Аполлоний показывает, что можно выбрать диаметр, который будет перпендикулярен к сопряженным с ним хордам. Тогда рассматриваемую кривую можно представить как сечение любого тупоугольного, либо остроугольного, либо прямоугольного конусов вращения плоскостью, перпендикулярной к образующей. Этим устанавливается тождество кривых, введенных Аполлонием, с каноническими сечениями, которые рассматривались до него.

Основная идея первой книги состоит в том, чтобы за основу классификации кривых принять свойства их алгебраических уравнений, и именно те которые остаются инвариантными при допустимых преобразованиях координат. Только в XIX в. Эта мысль понята до конца, когда Клейн в «Эрлангенской программе» установил новый взгляд на геометрию, как науку об инвариантах определенных групп преобразований плоскости или пространства.

Дальнейшее исследование конических сечений в трудах Аполлония

В последующих трех книгах Аполлоний развивает теорию конических сечений: выясняет основные свойства сопряженных диаметров асимптот, получает уравнение гиперболы относительно асимптот (xy=const) и устанавливает основные свойства фокусов эллипса и гиперболы. Здесь же впервые появляются полюсы и поляры относительно конических сечений: если из точки можно провести две касательные к коническому сечению, то прямая соединяющая точки касания, называется полярой данной точки, а точка полюсом этой прямой. Если передвигать полюс по прямой, пересекающей сечение, то поляра будет вращаться вокруг полюса этой прямой, если же передвигать полюс по прямой, не пересекающей сечение, то поляра тоже будет вращаться вокруг некоторой точки, причем в этом случае точку вокруг которой вращается поляра, и прямую, по которой движется полюс, также называют полюсом и полярой. В четвертой книге Аполлоний рассматривает вопрос о числе точек пересечения двух конических сечений.

В пятой книге Аполлоний определяет все нормали к коническому сечению (перпендикуляры к касательной, восстановленные в точке касания). В шестой книге изучаются подобные конические сечения.

В седьмой книге содержатся знаменитые теоремы Аполлония:

a)         сумма квадратов на сопряженных диаметрах эллипса равна сумме квадратов на главных осях;

b)         разность квадратов на двух сопряженных диаметрах гиперболы равна разности квадратов на главных осях;

c)         параллелограмм, построенный на двух сопряженных диаметрах эллипса или гиперболы, имеет постоянную площадь.

Дальнейшее развитие теории конических сечений

В древности методы исследования кривых созданные Аполлонием, не получили развития, хотя до начала V в. н.э. его труды изучались и комментировались. Что касается самих конических сечений, то они были применены еще Архимедом для решения и исследования кубического уравнения. Для тех же целей применяли конические сечения позднейшие античные геометры и ученые стран ислама.

В математическом естествознании долгое время не получили ни какого применения, если не считать изучение отражения света от параболических зеркал. Только в XVII в. наступило возрождение идей Аполлония: Ферма и Декарт перевели его метод на язык новой алгебры, основав аналитическую геометрию, а Ньютон, применил эти методы для описания и исследования кривых третьего порядка. Но еще раньше теория конических сечений получила самое широкое применение в механике земных и небесных тел: Кеплер установил, что планеты нашей солнечной системы движутся по эллипсам, в одном из фокусов которой находится Солнце; Галилей показал, что брошенный камень летит в пустоте по параболе. Наконец, в 80-х годах XVII в. Ньютон создал свои «Математические начала натуральной философии», непосредственно опираясь на труды Аполлония.

Заключение

Конические сечения Аполлонием являются примером математической теории, созданной задолго до того как она оказалась необходимой. По этому поводу А. Эйнштейн писал: «К восхищению перед этим замечательным человеком (речь идет о Кеплере) еще одно чувство восхищения и благоговения, но относящееся не к человеку, а к загадочной гармонии природы, которые соответствуют простейшим законам. Наряду с прямой и окружностью среди них были эллипс и гипербола. Последние мы видим реализованными в орбитах небесных тел, во всяком случае, с хорошим приближением».

Список литературы:

1.         Пути и лабиринты. Очерки по истории математики. Даан – Дальмедико А., Пейффер Ж. Пер. с франц. М.: Мир, 1986.

2.         История математики с древних времен до начала XIX столетия. Юшкевич А.П. – М.: Наука, 1970.