Учебное пособие: Амплитудно-частотные характеристики и настройка связанных контуров

Учебное пособие: Амплитудно-частотные характеристики и настройка связанных контуров

Академия России

Кафедра Физики

Лекция: Амплитудно-частотные характеристики и настройка

связанных контуров

Орел-2009

СОДЕРЖАНИЕ

Вступительная часть

АЧХ связных контуров при критической связи

АЧХ связных контуров при связи больше критической

Настройка и применение связных контуров

Заключение

Литература

Вступительная часть

В технике радиосвязи находят применение усилители со связанными контурами. Каскад подобного усилителя содержит усилительный прибор (транзистор или электронную лампу) и два, чаще всего одинаковых колебательных контура между которыми существует индуктивная или емкостная связь.

Приступим к исследованию АЧХ как функции частотной переменной x (обобщенной расстройки контура).

АЧХ СВЯЗАННЫХ КОНТУРОВ ПРИ КРИТИЧЕСКОЙ СВЯЗИ ()

Выражения АЧХ для связанных контуров с индуктивной и емкостной связями получились одинакового вида при соответствующих величинах, имеющих смысл, перечислены в прошлой лекции. Поэтому анализ АЧХ проведем по следующему выражению:

.

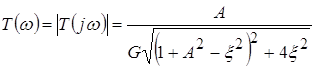При  выражение для АЧХ имеет вид:

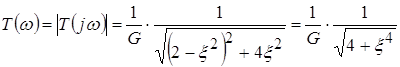
или .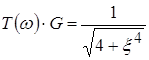

Функция , т. е. нормированное значение АЧХ имеет максимальное значение при . Это соответствует . Действительно:

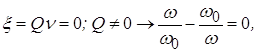 т. е.

Максимальное значение АЧХ будет равно:

.

По выражению  вычертим график (рисунок 1):

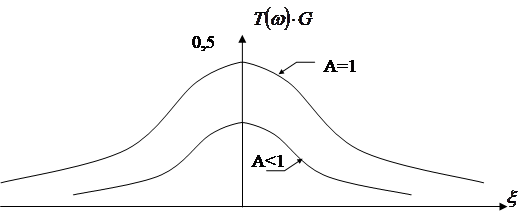Рис. 1.

При критической связи АЧХ получается максимально плоской.

Это можно пояснить исходя из формулы: при малых абсолютных значениях , т. е. при   входит в формулу в четвертой степени и мало влияет на знаменатель . С ростом  при  происходит резкое  изменение АЧХ, что является признаком улучшения избирательности.

Найдем ПП при критической связи. Т. к. ПП определяется на уровне 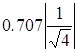  от максимального значения АЧХ (в рассматриваемом случае равного 0,5), то

.

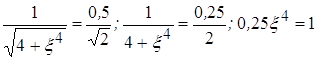Откуда  и  Т. к. то .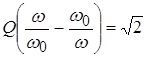

В силу геометрической симметрии резонансных характеристик колебательных контуров, выражение можно представить в виде:

.

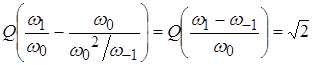Следовательно, ширина ПП связанных контуров при критической связи:

.

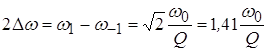Сравнивая данный результат с ПП одиночного контура, замечаем, что у связанных контуров, при критической связи ПП в  раз больше. Граничные частоты ПП определяются в предположении, что резонансная характеристика обладает арифметической симметрией, т. е.

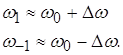
Можно показать (по аналогии с одиночным контуром), что  в этом случае меньше (), т. е. избирательность лучше, чем у одиночного контура ().

Примечание. Отметим, что 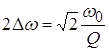 и  т. е. при  справедливо соотношение:

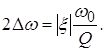
АЧХ СВЯЗАННЫХ КОНТУРОВ ПРИ СВЯЗИ БОЛЬШЕ КРИТИЧЕСКОЙ ()

В данном случае имеем три экстремальных значения АЧХ при

 .

Легко понять, что здесь имеет место один минимум и два максимума:

При  получим:

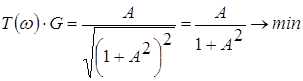 (т. к. ).

При  имеем:

.

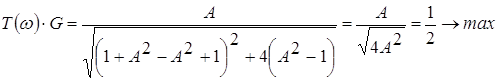График  при имеет вид (рис. 2).

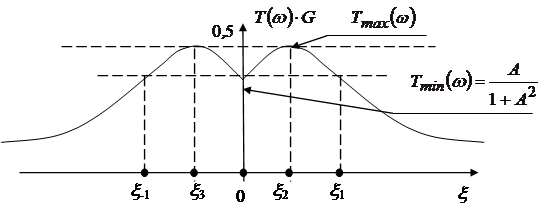
Рис. 2

Отношение 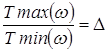 называют неравномерностью АЧХ связанных контуров. Если в это выражение подставить полученные выше значения max и min АЧХ получим:

.

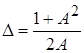Величина D зависит от параметра связи . При , т. е.  неравномерность АЧХ отсутствует.

Найдем ПП связанных контуров при связи больше критической.

Т. к. ПП определяется на уровне 0,707 от максимального значения АЧХ, а , то

,

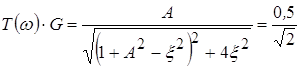и при этом неравномерность АЧХ имеет максимально допустимое значение  Найдем параметр связи  соответствующий этой наравномерности:

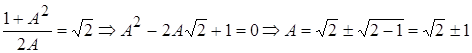
 (удовлетворяет условию )

 (не удовлетворяет условию ).

Подставив полученное значение  в исходное соотношение для АЧХ, получим величины  и , соответствующие граничным частотам ПП:

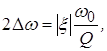 и . Т. к.  то ПП .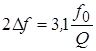

Граничные частоты ПП можно найти по приближенным формулам, отражающим арифметическую симметрию АЧХ:

 и .

Проведенный анализ показывает, что в зависимости от параметра связи  ПП связанных контуров может меняться в пределах

.

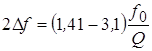где 1,41 – соответствует критической связи ();

3,1 – соответствует предельному значению ПП при связи большей критической ().

Выводы по первому и второму вопросам:

Важным преимуществом связанных контуров является то, что за пределами ПП их АЧХ убывает значительно быстрее чем у одиночного контура, т. е. избирательность их лучше (при ). Этим обеспечивается более совершенное подавление частот, которые лежат вне заданной ПП.

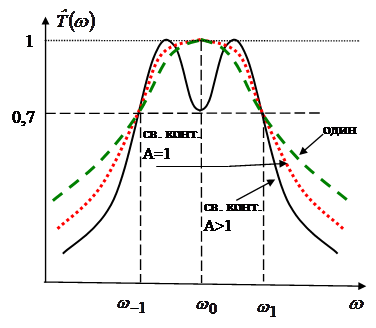
Рис. 3.

Приведем сравнительные данные для одиночного и связанных контуров (рисунок 3)

Пусть под заданную полосу пропускания  с заданной неравномерностью  рассчитаны одиночный колебательный контур и связанные контуры при критической и сильной связи. Тогда их АЧХ будет иметь вид, изображенный на рис. 3, причем максимальное значение каждой из характеристик принято считать равным единице.

Для получения одной и той же заданной полосы пропускания добротности контура должны быть различными: наибольшей будет добротность связанных контуров с сильной связью, меньшее значение имеет добротность связанных контуров при критической связи и наименьшее добротность одиночного контура.

Как видно, наилучшей избирательностью обладают связанные контуры при параметре связи .

Примечание: К. п. ф.

,

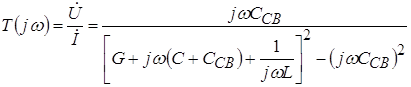м. б. представлена и построена как произведение 3-х к. п. ф.

Действительно, если знаменатель представить в виде разности квадратов, то получим

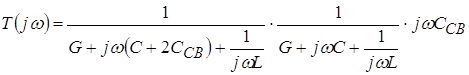
Тогда график результирующей АЧХ может быть построен как произведение  Обычно .

Рис. 4

Изменяя,  меняем расположение частоты ω0,1 (т. е. 1-го max). Если  мало, то ω0,1 и ω0,2 практически сливаются и результирующая кривая совпадает с графиком АЧХ одиночного контура, при некоторой связи () равной критической получаем максимально плоскую характеристику АЧХ (), а при связи большей критической – 2-х горбую” характеристику (). При дальнейшем увеличении  левый “горб” смещается по частоте влево () и график имеет  на частоте ω0,2, определяемой только элементами L и С.

НАСТРОЙКА И ПРИМЕНЕНИЕ СВЯЗАННЫХ КОНТУРОВ

Настройка системы связанных контуров заключается в подборе параметров контуров, обеспечивающих на заданной частоте получения максимального значения реакции на приложенное воздействие.

В случае внешнеемкостной связи задача сводится к получению максимального напряжения на контуре. Поскольку активные проводимости контуров, как правило, заданы и не подлежат изменению, процесс настройки сводится к подбору оптимальных значений реактивных параметров контуров.

Представим упрощенную эквивалентную схему связанных контуров с емкостной связью в виде (рис. 5).

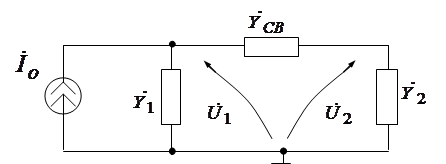
Рис. 5.

В этой схеме

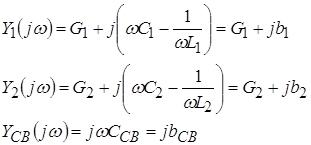
В зависимости от изменяемого реактивного параметра  и  или  определяют следующие виды настройки (резонанса):

– простой резонанс;

– сложный резонанс;

– основной (индивидуальный) резонанс;

– полный резонанс.

Дадим качественную характеристику каждого из этих резонансов, имя в виду, что настройка, как правило, ведется на критическую связь () (при которой АЧХ максимально плоская).

а) Простой резонанс

Настройка осуществляется одним из контуров: либо 1, либо-2. При этом имеет место 1-й частный резонанс, либо 2-й частный резонанс в зависимости от используемого для настройки контура (рис. 6).

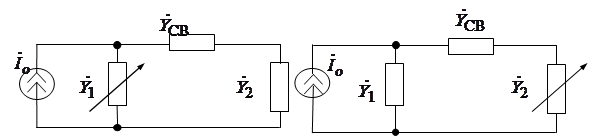
1-ый частотный резонанс             2-ой частотный резонанс

Рис. 6.

На практике настройка связанных контуров по методу получения простого резонанса осуществляется в тех случаях, когда меняется частота источника возбуждения. Например, настройка входных цепей приемников и выходных цепей некоторых передатчиков малой и средней мощности. Критерий настройки – наилучший эффект на выходе приемника или наибольший ток в антенне радиостанции.

б) Сложный резонанс.

Настройка осуществляется одним из контуров и емкостью связи  (рис. 7).

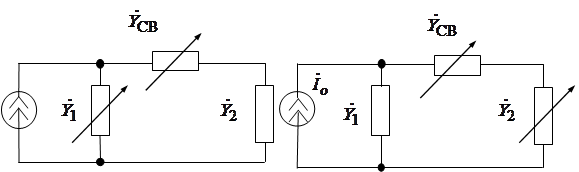
Рис. 7

Порядок настройки:

– при некотором значении  добиваются в одном из контуров простого резонанса (max показания вольтметра, подключенного к контуру, при изменении  или );

– изменением  добиваются больших показаний вольтметра.

Т. к. при изменении  нарушаются условия простого резонанса, то данные операции производят несколько раз до получения максимума.

Данный способ настройки применяется в выходном каскаде передатчиков средней и большой мощности (Р-102, Р-118, и др.).

в) Основной (индивидуальный) резонанс.

Настройка осуществляется в каждом контуре отдельно при закороченном другом контуре и при . (рисунок 8).

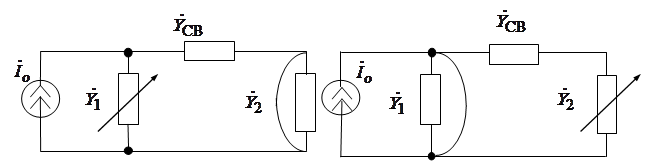
Рис. 8.

Порядок настройки:

– установить ;

– закоротить 2-й контур (при этом  подключить параллельно 1-му контуру);

– настроить 1-й контур на max напряжения, т. е. получить 1-й частный резонанс;

– аналогично настроить 2-й контур, закоротив 1-й, т. е. получить 2-й частный резонанс.

Данный метод применяется в заводских условиях для настройки селективных систем.

г) Полный резонанс.

Настройка выполняется после достижения основного резонанса, когда с помощью   добиваются max напряжения на контуре. При этом АЧХ получается максимально плоской.

Если требуется получить 2-х горбую характеристику, то связь между контурами увеличивают до тех пор, пока не будет получена допустимая неравномерность АЧХ ().

Настройка на полный резонанс применяется в трактах, где частота источника является неизменной, например в УПЧ.

При настройке должны быть приняты меры, чтобы ламповый вольтметр не шунтировал контур.

Отметим, что рассмотренные виды настройки применимы и к другим видам связанных контуров.

ЗАКЛЮЧИТЕЛЬНАЯ ЧАСТЬ

В лекции приведены АЧХ связанных контуров при сильной (А>1) и критической (А=1) связи, а также одиночного колебательного контура с одинаковыми ПП и неравномерностью характеристик. Сопоставление этих характеристик показывает, что за пределами ПП АЧХ связанных контуров убывают значительно быстрее, чем у одиночного колебательного контура. Тем самым обеспечивается более эффективное подавление тех гармонических составляющих воздействия, частоты которых лежат вне заданной ПП. Это объясняется тем, что связанные контуры, имея большее число элементов, позволяют получить более совершенные характеристики. Следует также отметить, что применение сильной связи позволяет получить большую крутизну спада АЧХ за пределами полосы пропускания, чем в случае критической связи при одинаковых неравномерностях в их полосах пропускания.

ЛИТЕРАТУРА

 1.Белецкий А. Ф. Теория линейных электрических цепей. – М.: Радио и связь, 1986.

2.Бакалов В. П. и др. Теория электрических цепей. – М.: Радио и связь, 1998;

3.Качанов Н. С. и др. Линейные радиотехнические устройства. М.: Воен. издат., 1974;

4. В. П. Попов Основы теории цепей М.: Высшая школа, 2000.