Учебное пособие: Гидравлика, гидропневмопривод

Учебное пособие: Гидравлика, гидропневмопривод

Министерство образования и науки Украины

Севастопольский национальный технический университет

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по дисциплине

«ГИДРАВЛИКА, ГИДРО-, ПНЕВМОПРИВОД»

для выполнения расчетно-графического задания №1

и самостоятельной работы студентов дневной

формы обучения

и контрольных работ студентов заочной формы обучения

специальности 7.090258

«Автомобили и автомобильное хозяйство»

Севастополь

2001

УДК 629.114.6

Методические указания по дисциплине «Гидравлика, гидро- и пневмопривод» по выполнению расчетно-графического задания №1 для студентов дневной формы обучения и контрольных работ для студентов заочной формы обучения специальности 7.090258 «Автомобили и автомобильное хозяйство»/ Сост. Ю.Л. Рапацкий.- Севастополь: Изд-во СевНТУ, 2001.- 16с.

Целью методических указаний является оказание помощи студентам специальности «Автомобили и автомобильное хозяйство» при изучении дисциплины «Гидравлика, гидро- и пневмопривод» и самостоятельном выполнении расчетно-графического задания №1 студентами дневной формы обучения и контрольных работ заочниками.

Методические указания предназначены для студентов специальности 7.090258 «Автомобили и автомобильное хозяйство» дневной и заочной форм обучения. Могут также использоваться студентами дневной и заочной форм обучения специальностей 7.090202 «Технология машиностроения» и 7.090203 «Металлорежущие станки и системы» при изучении ими соответствующих разделов аналогичной дисциплины.

Методические указания рассмотрены и утверждены на заседании кафедры АТИП (протокол №4 от 29.12.2001 г.)

Допущено учебно-методическим центром СевНТУ в качестве методических указаний.

Рецензент: Харченко А.О. канд. техн. наук, доцент кафедры Машиностроения и транспорта. Заслуженный изобритатель Украины.

Выбор вариантов на расчетно-графические задания для студентов дневной формы обучения и на контрольные работы для заочников

Студенты дневной формы обучения выполняют в течении семестра два расчетно-графических задания (РГЗ). Выбор вариантов – по последней цифре зачетной книжки. РГЗ оформляются в соответствии с действующими стандартами Украины для текстовых документов на стандартных листах формата А4. Допускается оформление РГЗ на листах в клетку, а схем и чертежей на миллиметровой бумаге. Рекомендуется использовать ПЭВМ для оформления РГЗ, в том числе целесообразно выполнять расчеты с применением одного из доступных математических пакетов типа Maple или Mathcad.

Защита студентами выполненных РГЗ производится индивидуально на консультациях, после проверки преподавателем правильности расчетов и оформления РГЗ.

РГЗ №1 должно быть защищено на 10-11 неделе семестра.

РГЗ №1 включает в себя пять задач в соотвествии с таблицей 1.

Таблица 1

Номера вариантов задач для первого РГЗ

При решении задач необходимо изобразить графически схемы и рисунки, поясняющие работу гидравлических устройств.

Студенты заочной формы обучения выполняют одну контрольную работу, в которую входят все задачи, которые включены в РГЗ №1 и РГЗ №2 ( выполняются по соотвествующим методическим указаниям). Выбор вариантов осуществляется аналогично приведенному выше.

1. ГИДРОСТАТИКА

Давление в неподвижной жидкости называется гидростатическим и обладает следующими двумя свойствами:

– на внешней поверхности жидкости оно всегда направленно по нормали внутрь объема жидкости;

– в любой точке внутри жидкости оно по всем направлениям одинаково, т.е. не зависит от угла наклона площадки, по которой действует.

Уравнение, выражающее гидростатическое давление P в любой точке неподвижной жидкости в том случае, когда из числа массовых сил на неё действует лишь одна сила тяжести, называется основным уравнением гидростатики:

P = Pa + hρg = Pa + γh, (1.1)

Где Pa – давление на какой либо поверхности уровня жидкости; h – глубина рассматриваемой точки, отсчитанная от поверхности с давлением Pa .

В тех случаях, когда рассматриваемая точка расположена выше поверхности с давлением Pa , второй член в формуле отрицателен. Другая форма записи того же уравнения имеет вид:

Где Z, Z0 – вертикальные координаты произвольной точки и свободной поверхности, отсчитываемые от горизонтальной поверхности; P/(ρg) – пьезометрическая высота.

Сила давления жидкости на плоскую стенку равна произведению гидростатического давления P на плоащдь стенки S

F=PS

Указания по решению задач.

При решении задач по гидростатике прежде всего нужно хорошо усвоить и не смешивать такие понятия как давление P и сила F. При решении задач на определение давления в той или иной точке неподвиджной жидкости следует пользоваться основным уравнением гидростатики. Применяя это уравнение, нужно иметь ввиду его второй член в правой части этого уравнения может быть как положительным так и отрицательным.

Необходимо твердо различать давления абсолютное, избыточное и вакуум, и обязательно знать связь между давлением, удельным весом и высотой, соответствующей этому давлению ( пьезометрической высотой).

При решении задач, в которых даны поршни или системы поршней, следует писать уравнение равновесия, т.е. равенство нулю всех сил, действующих на поршень.

Задача 1.1

Определиль силу давления жидкости (воды) на крышку люка диаметром D = 1м при показаниях манометра Pм = 0,08 Мпа, H0 = 1.5 м,

ρ = 1000 кг/м3.

Задача 1.2

Определить давление в гидросистеме и вес груза G, лежащего на поршне I1, если для его подъема к поршню I приложена сила F = 1 кН. Диаметры поршней D = 0,3 м; d = 0,08 м. Разностью высот пренебречь.

Задача 1.3

Определить давление Px жидкости, которую необходимо подвести к цилиндру, чтобы преодолеть усилие, направленное вдоль штока F = 1кН. Диаметры цилиндра D = 0,05 м, штока d = 0,025 м. Давление в бачке P0 = 50 кПа, высота H0 = 5 м. Силу трения не учитывать. Плотность жидкости ρ = 1000 кг/ м3.

Задача 1.4

Определить показание манометра Pм, если к штоку поршня приложена сила F = 0,1кН, его диаметр d = 0,1 м, высота H = 1.5 м. плотность жидкости ρ = 800 кг/ м3.

Задача 1.5

Определить силу F на штоке золотника, если показание вакуметра Pвак = 60 кПа, избыточное давление P1 = 1 Мпа, высота H = 3 м, диаметр поршней D = 0,02 м, d = 0,015 м; ρ = 1000 кг/ м3.

Задача 1.6

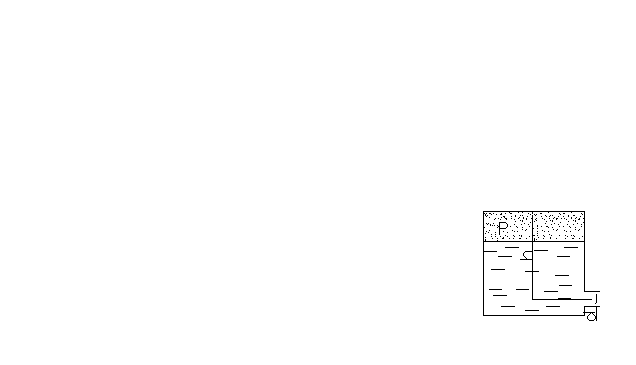
Определить давление P1, необходимое для удержания штоком трехпозиционного гидроцилиндра нагрузки F = 50 кН; давление P2 = P3 = 0,3 кПа; диаметры D = 0,04 м, d = 0,02 м.

Задача 1.7

Определить давление P1, необходимое для удержаниея цилиндром нагрузки F = 70 кН. Противодавление в полости 2 равно P2 = 0,3 МПа, давление полости 3 равно атмосферному. Размеры D4 = 0,08 м; Dш = 0,07 м, d1 = 0,05 м.

Задача 1.8

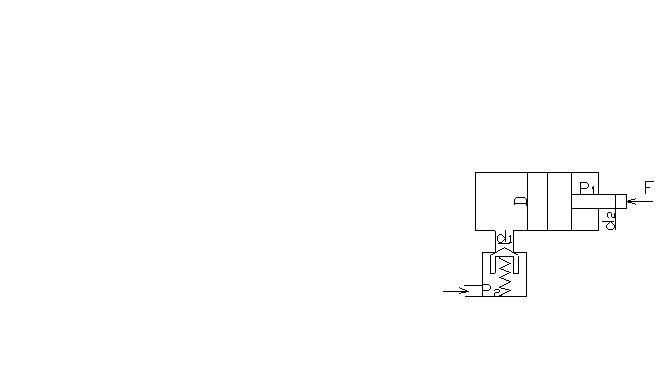
Определить минимальное значение силы F, приложеной к штоку, под действием которой начинается движение поршня диаметром D = 0,8 м, если сила пружины, прижимающая клапан к седлу, равна Fа = 100 Н, а давление жидкости P2 = 0,2 МПа. Диаметр входного отверстия клапана (седла) d1 = 0,01 м, даметр штока d2 = 0,04 м, давление жидкости в штоковой полости гидроцилиндра P1 = 1 МПа.

Задача 1.8

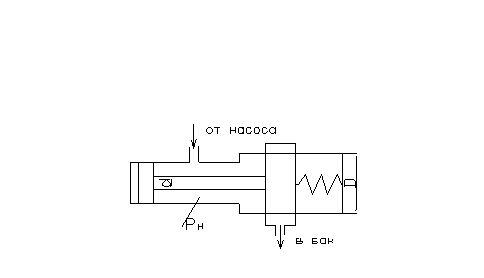
Определить величину предварительного поджатия пружины дифференциального предохранительного клапана (мм), обеспечивающую начало открытия клапана при P1 = 0,8 МПа. Диаметр клапана D = 0,024 м, d = 0,018 м; жесткость пружины С = 6 н/мм. Давление справа от большого и слева от малого поршней – атмосферное.

2. ПРИМЕНЕНИЕ УРАВНЕНИЯ БЕРНУЛЛИ

Основными уравнениями, позволяющими решать простейшие задачи о движении идеальной жидкости,являеться уравнение расхода и уравнение Бернулли.

Уравнение расхода основано на условии неразрывности потока жидкости и представляет собой равенство объемных расходов во всех сечениях потока

Q1 = Q2 или V1 S1 = V2 S2 (2.1)

где Q1 и Q2 – расходы в сечении потока площадью S1 , S2 ; V1 , V2 - скорости потока жидкости в этих сечениях.

Уравнение Бернулли для потока идеальной жидкости выражает собой закон сохранения удельной энергии жидкости вдоль потока. Уравнение Бернулли, отнесенное к еденице веса и записанное для сечения 1, 2, имеет вид:

где Z – вертикальные координаты центров тяжести сечений; P/ρg - пневмотическая высота (напор) ; V2/2g - скоростная высота (напор); H – полный напор.

Задача 2.1

Из напорного бака вода течет по трубе диаметром d1 = 0,02 м и затем вытекает в атмосферу через насадок с диаметром выходного отеврстия d2 = 0,01 м. Избыточное давление воздуха в баке P0 = 0,2 МПа; высота H = 1,6 м. Пренебрегая потерями энергии определить скорость течения жидкости (воды) в трубопроводе V1 и на выходе из насадки V2.

Задача 2.2

Определить расход керосина, вытекающего из бака по трубопроводу диаметром d = 0,05 м, если избыточное давление воздуха в баке P0 = 16 кПа; высота уровня H0 = 1 м; высота подъема керосина в пьезометре, открытом в атмосферу, H = 1,75 м. Потерями энергии принебречь. Плотность керосина ρ = 800 кг/ м3.

Задача 2.3

Жидкость вытекает из открытого резервуара в атмосферу через трубу, имеющую главное сужение до диаетра d1. Истечение происходит под действием напора H = 3 м. Пренебрегая потерями энергии, определить абсолютное давление в узком сечении трубы 1-1, если соотношение соответсвует h0 = 750 мм рт. ст. , плотность жидкости ρ = 1000 кг/ м3 . Найти напор Hкр, при котором абсолютное давление в сечении 1-1 будет равно нулю.

Указание: 1 мм рт. ст. – 133,3 Па. Уравнение Бернулли следует записать два раза, например, для сечения 0-0 и 2-2, а затем для сечения 1-1 и 2-2.

Задача 2.4

По длинной трубе диаметром d = 0,05 м протекает жидкость (ν = 2*10-4 м2/с; ρ = 900 кг/ м3 ). Определить расход жидкости и давление в сечении, где установлен пьезометр (h =0,6 м) и трубка П то (H = 0,8 м).

Задача 2.5

Вода течет по трубе диаметром D = 0,02 м, имеющей отвеод (d = 0,008 м). Пренебрегая потерями напора, определить расход жидкости в отводе Q1, если расход в основной трубе Q = 1,2*10-3 м3/с; высоты H = 2 м, h = 0,5 м. Режим течения указать турбулентным, ρ = 1000 кг/ м3.

Указание: считать, что давление перед отводом расходится на создание скоростного напора в отводе и подъем жидкости на высоту.

3.               ГИДРАВЛИЧЕСКИЕ ПОТЕРИ.

Различают два вида гидравлических потерь: местные потери и потери на трение по длине. Местные потери напора происходят в так называемых гидравлических сопротивлениях, т.е. в местных изменениях формы и размеров русла. Местны потери выражаются формулой Вейсбаха

hм = ξм . (3.1)

где V – средняя скорость потока в сечении перед местным сопротивлением или за ним; ξМ = безразмерный коэффициент местного сопративления.

Числовое значение коэффициента ξМ в основном определяется формой метсного сопративления, но иногда влияет число Рейнольдса, которое для труб диаметром d выражается формулой

Re = = (3.2)

где ν - кинематическая вязкость жидкости (м2/с).

При Re < Rе кр, где Rе кр ≈ 2300 режим движения ламинарный.

При Re > Rе кр – режим течения турбулентный.

Потери наопра на трение по длине l определяется ощей формулой Дарси

hпр = λ . V2/2g (3.3)

где λ – безразмерный коэффициент на трение по длине и определяется в зависимости от режима течения:

при ламинарном режиме λл однозначно определяется число Рейнольдса, т.е.

λл = (3.4)

Потери давления от местных сопротивлений определяются выражением

ΔP=ρg hм

(3.5)

ΔP= ξм ρ (3.6)

Если режим течения ламинарный, то потери давления по длине трубопровода считают по формуле Пуваейлля

ΔP= ν ρ Q (3.6)

где ν кинематическая вязкость жидкости; ρ – плотность жидкости; Q – расход жидкости через сечение трубопровода диаметром d.

Если режим течения турбулентный, то потери давления по дилне трубопроода считают по формуле Дарон-Вейсбаха

ΔP= λ ρ

Для гидравлических гладких труб

λ=0,315.Re-0,2

Задача 3.1

Определить потери давления в трубопроводе, если известно, что давление на его входе P = 0,4 МПа и коэффициент местных потерь ξ1 = 0,5;

ξ2 = 4,24; ξ3 = 0,2; ξ4 = 1,5. Плотность жидкости ρ = 900 кг/ м3 . Средняя скорость жидкости во всех сечениях трубопровода принять равной V = 2 м/с. Потерями на трение по длине пренебречь.

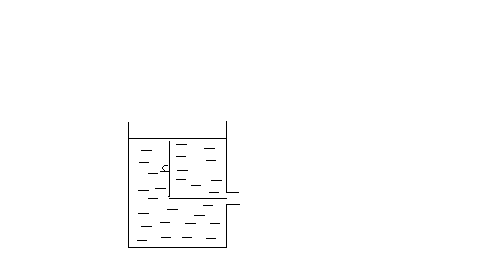
Задача 3.2

Определить потери давления на участке трубопровода, представленного на рис. 3.2, если известна скорость движения потока жидкости V = 3 м/с и плотность жидкости ρ = 1000 кг/ м3 . Коэффициенты местных поетрь ξ1 = 6; ξ2 = 1,2; ξ3 = 1,7; ξ4 = 0,8. ξ5 = 6. Потерями на трение по длине пренебречь.

Задача 3.3

Определить давление на выходе трубопровода длиной l = 3м и диаметром d = 0,03 м, если расход трубопровода Q = 1,5 *10 -3 м3/с, коэффициент кинематической вязкости жидкости ν= 3* 10-5 м2/с. Давление на входе трубопровода P = 0,4 МПа, ρ = 1000 кг/ м3 .

Задача 3.4

Рпеделить потери давления в трубопроводе длиной l = 5м и диаметром d = 0,01 м, если расход трубопровода Q = 4 *10 -3 м3/с, коэффициент кинематической вязкости жидкости ν= 3,6* 10-5 м2/с.

Задача 3.5

Трубопровод длиной l = 4 м и диаметром d = 0,05 м имеет расход Q = 1 *10 -3 м3/с, коэффициент кинематической вязкости жидкости

ν= 3* 10-5 м2/с. Давление на входе трубопровода P = 0,5 МПа. В конце участка трубопровода установлен патрубок с местными сопративлениями. Коэффициенты местных потерь ξ1 = 0,5; ξ2 = 0,8; ξ3 = 1,2; ρ = 800 кг/ м3 . Определить потери давления.

4. ИСТЕЧЕНИЕ ЖИДКОСТИ ЧЕРЕЗ ОТВЕРСТИЯ, НАСАДКИ, ДРОССЕЛИ

В процессе истечения жидкости происходит преобразование потенциальной энергии жидкости в кинетическую.

Из уравнения Бернулли легко выводится выражение для скорости истечения:

V=φ.

где H расчетный напор, который в общем уравнении равен сумме геометрического и пьезометрического напоров, т.е

H=ΔZ +

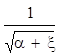φ – коэффициент скорости, определенный так

φ=

Здесь α коэффициент Керполиса; ξ – коэффициент местного сопративления.

Расход жидкости при истечении через отверстия, насадки, дроссели определяется произведением скорости течения на площадь сечения струи:

Q = μ. S0.

Указания к решению задач:

Отверстие в тонкой стенке для приближенных расчетов обычно принимают: φ = 0,97; α = 1; ξ = 0,065; μ = 0,62.

При внешнем цилиндрическом насадке μ = φ = 0,82; ξ = 0,5; α = 1.

Задача 4.1

Определить расход жидкости (ρ = 800 кг/ м3), вытекающей из бака через отверстие плащадью S0 = 1 см2 . Показание трутного прибора, измеряющего давление воздуха, h = 268 мм, высота H0 = 2 м, коэфициент расхода отверстия μ = 0,6 (1 мм рт. ст. = 133,3 Па).

Задача 4.2

Определить скорость перемещения поршня вниз, если к его штоку приложена сила F = 10 кН. Поршень диаметром D = 50 мм имеет пять отверстий диаметром d = 2 мм каждое. Отверстия рассматривать как внешние цилиндрические насадки с коэффициентом расхода μ = 0,82; ρ = 900 кг/ м3.

Задача 4.3

Определить скорость истечения жидкости через насадок диаметром d = 10 мм, если высота жидкости h = 1 м и плотность ρ = 900 кг/ м3 ,

Избыточное давление в баке P = 0,03 МПа.

Задача 4.4

Определить расход жидкости через насадок диаметром

d = 0,02 м, если высота жидкости h = 10 м и плотность ρ = 900 кг/ м3 , μ = 0,8. Считать объем бака неограниченым и падением высоты h пренебречь.

5.   ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ТРУБОПРОВОДОВ

В основе расчета трубопроводов лежат формула Дарси (3.3) для определения потерь напора на трение по длине и формула Вейсбаха (3.1) для местных потерь.

При ламинарном режиме течения вместо формулы (3.3) обычно бывает удобно пользоваться зависимостью, называемой законом Празеля

Формулу Дарси обычно выражают через расход и получают

Коэффициент Дарси при турбулентных режимах можно определить

Задача 5.1

Жидкость с плотностью ρ = 800 кг/ м3 и вязкостью ν= 2.10-4 м2/с подается на расстояние l = 20 м по горизонтальной трубе d = 0,02 м в количестве Q = 0,00157 м3/с. Определить давление и мощность, которые требуются для указанной подачи. Местные гидравлические сопротивления отсутствуют.

Задача 5.2

Керосин перекачивается по горизонтальной трубе длиной l = 50 м и диаметром d = 0,03 м в количестве Q = 0,0098 м3/с. Определить потребноедавление и необходимую мощность, если свойства керосина: ν= 0,025.10-4 м2/с; ρ = 800 кг/ м3 . Местными гидравлическими сопротивлениями пренебрегаем.

Задача 5.3

По трубопроводу диаметром d = 0,01 м и длиной l = 10 м подается жидкость с взякостью ν= 1.10-4 м2/с под действием перепада давления ΔP = 4 МПа; ρ = 1000 кг/ м3 . Определить режим движения жидкости в трубопроводе.

Задача 5.4

Определить режим течения жидкости при температуре 10 °С (ν= 0,4*10-4 м2/с) по трубопроводу длиной l = 3 м, который при перепаде давления ΔP = 2 МПа должен обеспечить расход Q = 0,001 м3/с. Плотность ρ = 850 кг/ м3 ; d = 0,02 м.

Задача 5.5

При каком Диаметре трубопровода подача насоса составит Q =1. 10-8 м3/с, если на выходе из него напор распыляется на 9,6 м; длина трубопровода l = 10 м; давление в баке P0 = 30 кПа; высота H0 = 4 м; вязкость жидкости ν= 1,5.10-6 м2/с и её плотность ρ = 1000 кг/ м3 . Метсными гидравлическими сопротивлениями пренебречь.

ЛИТЕРАТУРА

1.         Федорец В.А. , Подченко М.Н. и др. Гидроприводы и гидропневмоавтоматика станков. – К. : Виша шк. Головное изд-во1987. – 365с.

2.         Некрасов Б.Б. Задачник по гидравлике, гидромашинам и гидроприводу. – М. : Высш. шк. , 1989. 192с.