
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Контрольная работа: Финансовая математика
Контрольная работа: Финансовая математика
Задание 1
Правило торговца.
Кредит в Z = 15 000 руб. выдан на N = 10 месяцев под i = 10% годовых. Договор предусматривает погашение двумя промежуточными платежами. Первая выплата в сумме R1 = 600 руб. производится через n1 = 6 месяцев, вторая выплата в сумме R2 = 9 000 руб. - через n2 = 9 месяцев. Найти выплату в конце срока кредита.
Решение.
Продолжительность кредита в долях года равна
T =10/12=5/6.
Тогда долг (кредит с процентами) составит 15 000(1 + 0,1⋅0,83) = 16 245.
Интервал времени (в долях года) от момента первого платежа до окончания срока кредита
t1 =(10-6) /12=1/3.
Сумма первого платежа с процентами равна
R1=(1+ i t1) = 600(1+0,1·1/3) =620.
Остаток долга после первого платежа будет равен
Z1 = 16245-620=15625.
Интервал времени (в долях года) от момента второго платежа до окончания срока кредита
t2 =(10-9) /12=1/12.
Сумма второго платежа с процентами равна
R2=(1+ i t2) =9000(1+0,1·1/12) =9075.
Остаток долга будет равен
Z2 = 15625-9075=6550.
Отсюда следует, что в конце срока кредита погашающий платеж равен
R3= 6550 руб.
Таким образом, заемщиком будет выплачена сумма
R1+ R2+R3= 600+9000+6550=16150 руб.
При этом его долг кредитору составляет 16 245 руб.
Задание 2
Клиент получил ссуду Р = 200000 руб. сроком на n = 8 лет под 6% процентов годовых. Погашение кредита производится в конце каждого года равными долями.
Вычислить размер ежегодного платежа и его разбиение на погашение основного долга и погашение процентов. Вычисления по формулам проверить с помощью функций ПЛТ, ОСПЛТ, ПРПЛТ.
Решение.
Клиент должен каждый год выплачивать банку сумму
R=P∙ i/(1-(1+i) - n) =200000∙0,06/(1-(1+0,06) - 8) =32207, 19
Этот ответ можно получить, используя таблицу коэффициентов приведения a(i,k),
R=P/(a(6%,8)) =200000/6, 20979=32207, 19
найдем выплаты по процентам и основного долга в конце первого года, т.е. при j = 1, Z0 = P = 200 000:
D1 = i·Z0 = 0,06·200 000 = 12 000,B1 = R - D1 = 32207,19 - 12000 =20207, 19.
Тогда остаток долга в конце первого года будет равен
Z1 = Z0 - B1 = 200 000 - 20207,19 = 179792,81.
В конце второго года, т.е. при j = 2 выплаты по процентам
D2 = i·Z1 = 0,06·179792,81 ≈ 10787,57,выплаты основного долга
B2 = R - D2 = 32207,19 - 10787,57 = 21419,62.
Тогда остаток долга в конце второго года будет равен
Z2= Z1 - B2 = 179792,81 - 21419,62 = 158373, 19.
В конце третьего года, т.е. при j = 3 выплаты по процентам
D3= i·Z2 = 0,06·158373,19 ≈ 9502,39,
выплаты основного долга
B3 = R - D3 =32207,19 -9502,39= 22704,8.
Тогда остаток долга в конце третьего года будет равен
Z3 = Z2 - B3 = 158373,19 - 22704,8 =135668,39.
В конце четвертого года, т.е. при j = 4 выплаты по процентам
D4 = i·Z3 = 0,06·135668,39 =8140,10,выплаты основного долга
B4 = R - D4 =32207,19 -8140,10= 24067,08.
Тогда остаток долга в конце четвертого года будет равен
Z4 = Z3 - B4 = 135668,39 - 24067,08 = 111601,31.
В конце пятого года, т.е. при j = 5 выплаты по процентам
D5 = i·Z4 = 0,06·111601,31 =6696,08,выплаты основного долга
B5 = R - D5 =32207,19 -6696,08= 25511,11.
Тогда остаток долга в конце пятого года будет равен
Z5 = Z4 - B5 = 111601,31 - 25511,11 = 86090,2.
В конце шестого года, т.е. при j = 6 выплаты по процентам
D6 = i·Z5 = 0,06·86090,2 =5165,41,выплаты основного долга
B6 = R - D6 =32207,19 -5165,41= 27041,78.
Тогда остаток долга в конце шестого года будет равен
Z6 = Z5 - B6 = 86090,2 - 27041,78= 59048,42.
В конце седьмого года, т.е. при j = 7 выплаты по процентам
D7 = i·Z6 = 0,06·59048,42=3542,91,выплаты основного долга
B7 = R - D7 =32207,19 -3542,91= 28664,28.
Тогда остаток долга в конце седьмого года будет равен
Z7 = Z6 - B7 = 59048,42 - 28664,28= 30384,14.
В конце восьмого года, т.е. при j = 8 выплаты по процентам
D8 = i·Z7 = 0,06·30384,14 =1823,05,выплаты основного долга
B8 = R - D8 =32207,19 -1823,05= 30384,14.
Тогда остаток долга в конце восьмого года будет равен
Z8 = Z7 - B8 = 30384,14 - 30384,14= 0.
Теперь проверим вычисления с помощью функций ПЛТ, ОСПЛТ, ПРПЛТ
| кредит | 200 000,00 | ||||
| срок | 8 | ежегодная выплата R | |||
| проц ставка | 6% | -32 207, 19р. | |||
| год | основные Bi | проценты Di | остатки долга Zi | ||
| 0 | 200 000,00 | ||||
| 1 | -20 207, 19р. | -12 000,00р. | 179 792,81р. | ||
| 2 | -21 419,62р. | -10 787,57р. | 158 373, 19р. | ||
| 3 | -22 704,80р. | -9 502,39р. | 135 668,39р. | ||
| 4 | -24 067,08р. | -8 140,10р. | 111 601,31р. | ||
| 5 | -25 511,11р. | -6 696,08р. | 86 090, 20р. | ||
| 6 | -27 041,78р. | -5 165,41р. | 59 048,42р. | ||
| 7 | -28 664,28р. | -3 542,91р. | 30 384,14р. | ||
| 8 | -30 384,14р. | -1 823,05р. | 0,00р. | ||
Задание 3
Проект рассчитан на два года и требует инвестиции в I0 = $ 15 000. В конце первого года доход составит R1= $ 7 000, а в конце второго года - R2= $ 12 000.
Найти при заданной ставке приведения i=10%:
1) чистый приведенный доход NPV;
2) чистый наращенный доход NFV;
3) cрок окупаемости без учета и с учетом времени;
4) внутреннюю ставку дохода.
Вычисления по формулам проверить помощью функций ЧПС и ВСД.
Решение.
Из формулы при n = 2, i = 10% найдем чистый приведенный доход n
NPV=∑ * Rk / (1+i) k-I0
k=1
NPV=7000/1,1+12000/1,12-15000=6363,64+9917,36-15000=1281
или NPV=R1*v(10%,1) +R2*v(10%,2) - I0
=7000*0,909091+12000*0,826446-15000=6363,64+9917,36-15000=1281
Заметим, что величина $ 6363,64 соответствует современной стоимости $ 7 000, а величина инвестиции $ 9 917,36 соответствует современной стоимости $ 12 000.
NFV = (1+i) 2 ·NPV = 1,12 · 1281 = 1550,01
Найдем срок окупаемости без учета времени по формуле
R1+R2+…+R [nok] +R [nok] +1=I0,
что приводит к уравнению
7000 + 12000x = 15 000.
Отсюда дробная часть срока окупаемости
x=7000/12000=0,58
Срок окупаемости равен 1 + x = 1,58.
Срок окупаемости с учетом времени по формуле:
v(i,1) R1+v(i,2) R2+…+v(i, [nok]) R [nok] +xv(i, [nok] +1) R [nok] +1=I0
приводит к уравнению
7000/1,1+12000/1,12x=15000; 7000*v(10%,1) +12000*v(10%,2) x=15000;
6363,64+9917,36x=15000; x=(15000-6363,64) /9917,36=0,87
Срок окупаемости с учетом времени поступления доходов равен 1,87.
Внутреннюю ставку дохода по определению находим из решения уравнения относительно i.
7000/(1+i) +12000/(1+i) 2=15000 или
15000х2-7000х-12000=0
где x = 1 + i. Сокращая на 1000, получим квадратное уравнение
15x2 - 7x - 12 = 0.
Положительный корень этого уравнения x1= 1,1577
Отсюда находим, что внутренняя ставка дохода
IRR = x1- 1 = 1,1577 - 1 =0,1577.
Вычисления по формулам проверим в Excel с помощью функций ЧПС и ВСД.
| Исходные данные | ||||
| ставка приведения | инвестиции | доходы | ||
| в конце 1 года | в конце 2 года | |||
| 10% | -15 000,00р. | 7000 | 12000 | |
| Решение | ||||
| приведенные доходы | 16 280,99р. | |||
| чистый приведенный доход | 1 280,99р. | |||
| внутренняя ставка дохода | 16% | |||
Задание 4
На финансовом рынке может сложиться одна из четырех ситуаций A1, A2, A3, A4.
В условиях полной неопределенности инвестор выбирает из четырех финансовых операций F1, F2, F3, F4. Доходы инвестора определяются матрицей
![]()

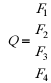
Определить оптимальный выбор финансовой операции по критериям Вальда и Сэвиджа.
1. Оптимальный выбор финансовой операции по критерию Вальда.
Найдем наихудший исход каждой финансовой операции, т.е. определим наименьшее число в каждой строке матрицы доходов:
a1= 14, a2= 8, a3= 11, a4= 12.
Согласно правилу Вальда, наибольшее среди найденных чисел определяет оптимальный доход. Следовательно, оптимальный доход равен 14, и он гарантируется выбором финансовой операции F1.
2. Оптимальный выбор финансовой операции по критерию Сэвиджа.
Сначала получим из матрицы доходов матрицу рисков. Для этого в каждом столбце матрицы доходов найдем наибольшее число
b1=17, b2=18, b3=18, b4=17.
Вычитая из наибольшего значения столбца все его элементы, получаем столбец матрицы рисков. Следовательно, матрица рисков имеет вид
Q=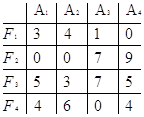
Найдем наихудший исход каждой финансовой операции, т.е. определим наибольший риск в каждой строке матрицы рисков:
q1= 4, q2= 9, q3= 7, q4= 6.
Согласно правилу Сэвиджа наименьшее среди найденных чисел определяет оптимальный доход. Следовательно, оптимальный доход равен 4, и он гарантируется выбором финансовой операции F1.
© 2009 База Рефератов