
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Контрольная работа: Оценка значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента
Контрольная работа: Оценка значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента
Содержание
Введение. 2
1. Оценка значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента. 3
2. Расчет значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента. 6
Заключение. 15
Список литературы.. 16
Введение
Актуальность работы состоит в том, что оценку значимости отдельных коэффициентов уравнения регрессии с помощью t-статистики Стьюдента применяют во всевозможных отраслях, начиная от математических вычислений и заканчивая промышленностью.
Целью нашей работы стоит рассмотрение оценки значимости отдельных коэффициентов уравнения регрессии с помощью t-статистики Стьюдента.
Для этого нужно решить следующие вопросы:
1. Оценка значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента
2. Расчет значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента
1. Оценка значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента
Необходимость применения многофакторного корреляционного анализа. Этапы многофакторного корреляционного анализа. Правила отбора факторов для корреляционной модели. Обоснование необходимого объема выборки данных для корреляционного анализа. Сбор и статистическая оценка исходной информации. Способы обоснования уравнения связи. Основные показатели связи в корреляционном анализе и их интерпретация. Сущность парных (общих), частных и множественных коэффициентов корреляции и детерминации. Оценка значимости коэффициентов корреляции. Порядок расчета уравнения множественной регрессии шаговым способом. Интерпретация его параметров. Назначение коэффициентов эластичности и стандартизированных бетта-коэф-фициентов. [1]
После построения уравнения регрессии необходимо сделать проверку его значимости: с помощью специальных критериев установить, не является ли полученная зависимость, выраженная уравнением регрессии, случайной, т.е. можно ли ее использовать в прогнозных целях и для факторного анализа. В статистике разработаны методики строгой проверки значимости коэффициентов регрессии с помощью дисперсионного анализа и расчета специальных критериев (например, F-критерия). Нестрогая проверка может быть выполнена путем расчета среднего относительного линейного отклонения (ё), называемого средней ошибкой аппроксимации:
Перейдем теперь к оценке значимости коэффициентов регрессии bj и построению доверительного интервала для параметров регрессионной модели Ру (J=l,2,..., р).
Блок 5 - оценка значимости коэффициентов регрессий по величине ^-критерия Стьюдента. Расчетные значения ta сравниваются с допустимым значением
Блок 5 - оценка значимости коэффициентов регрессий по величине ^-критерия. Расчетные значения t0n сравниваются с допустимым значением 4,/, которое определяется по таблицам t - распределения для заданной вероятности ошибок (а) и числа степеней свободы (/).
Кроме проверки значимости всей модели, необходимо провести проверки значимости коэффициентов регрессии по /-критерию Стюдента. Минимальное значение коэффициента регрессии Ьг должно соответствовать условию bifob- ^t, где bi - значение коэффициента уравнения регрессии в натуральном масштабе при i-ц факторном признаке; аь. - средняя квадратическая ошибка каждого коэффициента. несопоставимость между собой по своей значимости коэффициентов D;
Дальнейший статистический анализ касается проверки значимости коэффициентов регрессии. Для этого находим значение ^-критерия для коэффициентов регрессии. В результате их сравнения определяется наименьший по величине ^-критерий. Фактор, коэффициенту которого соответствует наименьший ^-критерий, исключается из дальнейшего анализа.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стъюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Но о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:
Оценка значимости коэффициентов чистой регрессии с помощью /-критерия Стьюдента сводится к вычислению значения
Качество труда - характеристика конкретного труда, отражающая степень его сложности, напряженности (интенсивности), условия и значимость для развития экономики. К.т. измеряется посредством тарифной системы, позволяющей дифференцировать заработную плату в зависимости от уровня квалификации (сложности труда), условий, тяжести труда и его интенсивности, а также значимости отдельных отраслей и производств, районов, территорий для развития экономики страны. К.т. находит выражение в заработной плате работников, складывающейся на рынке труда под воздействием спроса и предложения рабочей силы (конкретные виды труда). К.т. - сложная по структуре
Полученные баллы относительной значимости отдельных экономических, социальных и экологических последствий осуществления проекта дают далее основу для сравнения альтернативных проектов и их вариантов с помощью "комплексного балльного безразмерного критерия социальной и эколого-экономической эффективности" проекта Эк, рассчитываемого (в усредненных баллах значимости) по формуле
Внутриотраслевое регулирование обеспечивает различия в оплате труда работников данной отрасли промышленности в зависимости от значимости отдельных .видов производства данной отрасли, от сложности и условий труда, а также от применяемых форм оплаты труда.
Полученная рейтинговая оценка анализируемого предприятия по отношению к предприятию-эталону без учета значимости отдельных показателей является сравнительной. При сравнении рейтинговых оценок нескольких предприятий наивысший рейтинг имеет предприятие с минимальным значением полученной сравнительной оценки.
Понимание качества товара как меры его полезности ставит практически важный вопрос об её измерении. Его решение достигается изучением значимости отдельных свойств в удовлетворении определенной потребности. Значимость даже одного и того же свойства может быть неодинаковой в зависимости от условий потребления продукта. Следовательно, и полезность товара в разных обстоятельствах её использования различна.
Второй этап работы - изучение статистических данных и выявление взаимосвязи и взаимодействия показателей, определение значимости отдельных факторов и причин изменения общих показателей. [2]
Все рассматриваемые показатели сводятся в один таким образом, что в результате получается комплексная оценка всех анализируемых сторон деятельности предприятия с учетом условий его деятельности, с учетом степени значимости отдельных показателей для различных типов инвесторов:
Коэффициенты регрессии показывают интенсивность влияния факторов на результативный показатель. Если проведена предварительная стандартизация факторных показателей, то Ь0 равняется среднему значению результативного показателя в совокупности. Коэффициенты Ь,, Ь2 ..... Ьл показывают, на сколько единиц уровень результативного показателя отклоняется от своего среднего значения, если значения факторного показателя отклоняются от среднего, равного нулю, на одно стандартное отклонение. Таким образом, коэффициенты регрессии характеризуют степень значимости отдельных факторов для повышения уровня результативного показателя. Конкретные значения коэффициентов регрессии определяют по эмпирическим данным согласно методу наименьших квадратов (в результате решения систем нормальных уравнений).
2. Расчет значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента
Рассмотрим линейную форму многофакторных связей не только как наиболее простую, но и как форму, предусмотренную пакетами прикладных программ для ПЭВМ. Если же связь отдельного фактора с результативным признаком не является линейной, то производят линеаризацию уравнения путем замены или преобразования величины факторного признака.
Общий вид многофакторного уравнения регрессии имеет вид:
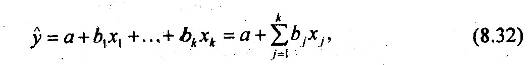
где k - число факторных признаков.
Чтобы упростить систему уравнений МНК, необходимую для вычисления параметров уравнения (8.32), обычно вводят величины отклонений индивидуальных значений всех признаков от средних величин этих признаков.
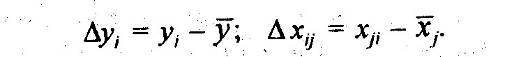
Получаем систему k уравнений МНК:
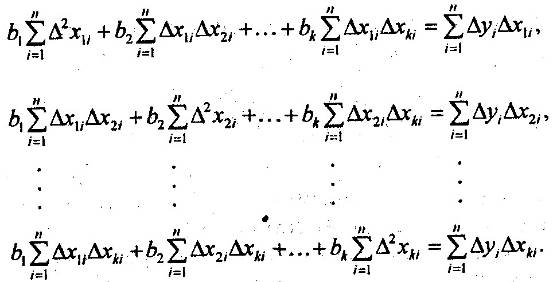
Решая эту систему, получаем значения коэффициентов условно-чистой регрессии b. Свободный член уравнения вычисляется по формуле

Термин «коэффициент условно-чистой регресии» означает, что каждая из величин bj измеряет среднее по совокупности отклонение результативного признака от его средней величины при отклонении данного фактора хj от своей средней величины на единицу его измерения и при условии, что все прочие факторы, входящие в уравнение регрессии, закреплены на средних значениях, не изменяются, не варьируют.
Таким образом, в отличие от коэффициента парной регрессии коэффициент условно-чистой регрессии измеряет влияние фактора, абстрагируясь от связи вариации этого фактора с вариацией остальных факторов. Если было бы возможным включить в уравнение регрессии все факторы, влияющие на вариацию результативного признака, то величины bj. можно было бы считать мерами чистого влияния факторов. Но так как реально невозможно включить все факторы в уравнение, то коэффициенты bj. не свободны от примеси влияния факторов, не входящих в уравнение.
Включить все факторы в уравнение регрессии невозможно по одной из трех причин или сразу по ним всем, так как:
1) часть факторов может быть неизвестна современной науке, познание любого процесса всегда неполное;
2) по части известных теоретических факторов нет информации либо таковая ненадежна;
3) численность изучаемой совокупности (выборки) ограничена, что позволяет включить в уравнение регрессии ограниченное число факторов.[3]
Коэффициенты условно-чистой регрессии bj. являются именованными числами, выраженными в разных единицах измерения, и поэтому несравнимы друг с другом. Для преобразования их в сравнимые относительные показатели применяется то же преобразование, что и для получения коэффициента парной корреляции. Полученную величину называют стандартизованным коэффициентом регрессии или ?-коэффициентом.

?-коэффициент при факторе хj, определяет меру влияния вариации фактора хj на вариацию результативного признака у при отвлечении от сопутствующей вариации других факторов, входящих в уравнение регрессии.
Коэффициенты условно-чистой регрессии полезно выразить в виде относительных сравнимых показателей связи, коэффициентов эластичности:

Коэффициент эластичности фактора хj говорит о том, что при отклонении величины данного фактора от его средней величины на 1% и при отвлечении от сопутствующего отклонения других факторов, входящих в уравнение, результативный признак отклонится от своего среднего значения на ej процентов от у. Чаще интерпретируют и применяют коэффициенты эластичности в терминах динамики: при увеличении фактора х.на 1% его средней величины результативный признак увеличится на е. процентов его средней величины.
Рассмотрим расчет и интерпретацию уравнения многофакторной регрессии на примере тех же 16 хозяйств (табл. 8.1). Результативный признак - уровень валового дохода и три фактора, влияющих на него, представлены в табл. 8.7.
Напомним еще раз, что для получения надежных и достаточно точных показателей корреляционной связи необходима более многочисленная совокупность.
Таблица 8.7
Уровень валового дохода и его факторы
| Номера хозяйств | Валовой доход, руб./ra у | Затраты труда, чел.-дни/га х1 |
Доля пашни, % x2 |
Надой молока на 1 корову, кг, x3 |
| 1 | 704 | 265 | 45,1 | . 3422 |
| 2 | 293 | 193 | 35,1 | 1956 |
| 3 | 346 | 229 | 69,4 | 2733 |
| 4 | 420 | 193 | 60,2 | 3254 |
| 5 | 691 | 225 | 59,0 | 3323 |
| 6 | 679 | 255 | 63,4 | 3179 |
| 7 | 457 | 201 | 58,1 | 3073 |
| 8 | 503 | 208 | 51,8 | 3257 |
| 9 | 314 | 170 | 73,2 | 2669 |
| 10 | 803 | 276 | 59,0 | 4235 |
| 11 | 691 | 188 | 42,5 | 3790 |
| 12 | 775 | 232 | 50,5 | 3658 |
| 13 | 584 | 173 | 48,6 | 3801 |
| 14 | 504 | 183 | 51,9 | 3266 |
| 15 | 777 | 236 | 58,9 | 5173 |
| 16 | 1138 | 265 | 38,8 | 5526 |
| Сумма | 9679 | 3492 | 865,5 | 56315 |
| Средняя | 604,9 | 218,2 | 54,1 | 3520 |
| s | 221,9 | 34,6 | 10,6 | 887 |
| v,% | 36,7 | 15,9 | 19,6 | 25,2 |
Таблица 8.8 Показатели уравнения регрессии
| Dependent variable: у | |||||
| Var. | Regression coefficient | Std. error | T(DF=12) | Prob. | Partial г2 |
| Х1 | 2,260978 | ,680030 | 3,325 | ,00606 | ,4795 |
| х2 | -4,307303 | 1,982283 | -2,173 | ,05053 | ,2824 |
| хЗ | ,166091 | ,027050 | 6,140 | ,00005 | ,7586 |
| Constant-240,112905 | |||||
| Std. error оf est. = 79,243276 | |||||
Решение проведено по программе «Microstat» для ПЭВМ. Приведем таблицы из распечатки: табл. 8.7 дает средние величины и средние квадратические отклонения всех признаков. Табл. 8.8 содержит коэффициенты регрессии и их вероятностную оценку:
первая графа «var» - переменные, т. е. факторы; вторая графа «regression coefficient» - коэффициенты условно-чистой регрессии bj; третья графа «std. errror» - средние ошибки оценок коэффициентов регрессии; четвертая графа - значения t-критерия Стьюдента при 12 степенях свободы вариации; пятая графа «prob» - вероятности нулевой гипотезы относительно коэффициентов регрессии;
шестая графа «partial r2» — частные коэффициенты детерминации. Содержание и методика расчета показателей в графах 3-6 рассматриваются далее в главе 8. «Constant» - свободный член уравнения регрессии a; «Std. error of est.» - средняя квадратическая ошибка оценки результативного признака по уравнению регрессии. Было получено уравнение множественной регрессии:
у= 2,26x1 - 4,31х2 + 0,166х3 - 240.
Это означает, что величина валового дохода на 1 га сельхозугодий в среднем по совокупности возрастала на 2,26 руб. при увеличении затрат труда на 1 ч/га; уменьшалась в среднем на 4,31 руб. при возрастании доли пашни в сельхозугодиях на 1% и увеличивалась на 0,166 руб. при росте надоя молока на корову на 1 кг. Отрицательная величина свободного члена вполне закономерна, и, как уже отмечено в п. 8.2, результативный признак - валовой доход становится нулевым задолго до достижения нулевых значений факторов, которое в производстве невозможно.
Отрицательное значение коэффициента при х^ - сигнал о существенном неблагополучии в экономике изучаемых хозяйств, где растениеводство убыточно, а прибыльно только животноводство. При рациональных методах ведения сельского хозяйства и нормальных ценах (равновесных или близких к ним) на продукцию всех отраслей, доход должен не уменьшаться, а возрастать с увеличением наиболее плодородной доли в сельхозугодиях - пашни.
На основе данных предпоследних двух строк табл. 8.7 и табл. 8.8 рассчитаем р-коэффициенты и коэффициенты эластичности согласно формулам (8.34) и (8.35).[4]
Как на вариацию уровня дохода, так и на его возможное изменение в динамике самое сильное влияние оказывает фактор х3 - продуктивность коров, а самое слабое - х2 - доля пашни. Значения Р2/ будут использоваться в дальнейшем (табл. 8.9);
Таблица 8.9 Сравнительное влияние факторов на уровень дохода
| Факторы хj | j | .ej | 2j |
| x1 | 0,352 | 0,816 | 0,138 |
| x2 | -0,206 | -0,385 | 0,042 |
| x3 | 0,664 | 0,966 | 0,441 |

Итак, мы получили, что ?-коэффициент фактора хj относится к коэффициенту эластичности этого фактора, как коэффициент вариации фактора к коэффициенту вариации результативного признака. Поскольку, как видно по последней строке табл. 8.7, коэффициенты вариации всех факторов меньше коэффициента вариации результативного признака; все ?-коэффициенты меньше коэффициентов эластичности.
Рассмотрим соотношение между парным и условно-чистым коэффициентом регрессии на примере фактора -с,. Парное линейное уравнение связи у с х, имеет вид:
y = 3,886x1 – 243,2
Условно-чистый коэффициент регрессии при x1, составляет только 58% парного. Остальные 42% связаны с тем, что вариации x1 сопутствует вариация факторов x2 x3, которая, в свою очередь, влияет на результативный признака. Связи всех признаков и их коэффициенты парных регрессий представлены на графе связей (рис. 8.2).
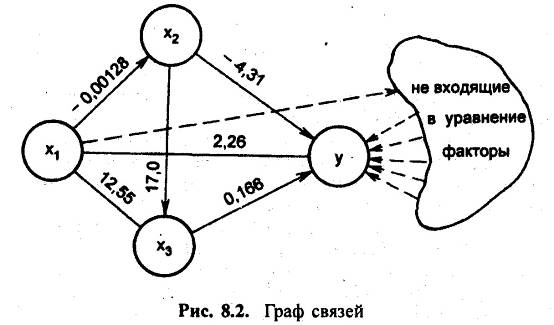
Если сложить оценки прямого и опосредованного влияния вариации х1 на у, т. е. произведения коэффициентов парных регрессий по всем «путям» (рис. 8.2), получим: 2,26 + 12,55·0,166 + (-0,00128)·(-4,31) + (-0,00128)·17,00·0,166 = 4,344.
Эта величина даже больше парного коэффициента связи x1 с у. Следовательно, косвенное влияние вариации x1 через не входящие в уравнение признаки-факторы - обратное, дающее в сумме:
3,886 - 4,344 = - 0,458.
Заключение
Итак, мы рассмотрели оценку значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента и вывели расчет значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента в работе также указана актуальность данных вычеслений.
В работе рассматриваются только самые общие вопросы этой сложной проблемы и дается начальное представление о методике построения уравнения множественной регрессии и показателей связи.
1 Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. Учебник для вузов. - М.: ЮНИТИ, 2008,– 311с.
2 Джонстон Дж. Эконометрические методы. - М.: Статистика, 1980,. – 282с.
3 Доугерти К. Введение в эконометрику. - М.: ИНФРА-М, 2004, – 354с.
4 Дрейер Н., Смит Г., Прикладной регрессионный анализ. - М.: Финансы и статистика, 2006,– 191с.
5 Магнус Я.Р., Картышев П.К., Пересецкий А.А. Эконометрика. Начальный курс.-М.: Дело, 2006, – 259с.
6 Практикум по эконометрике/Под ред. И.И.Елисеевой.- М.: Финансы и статистика, 2004, – 248с.
7 Эконометрика/Под ред. И.И.Елисеевой.- М.: Финансы и статистика, 2004, – 541с.
8 Кремер Н., Путко Б. Эконометрика.- М.:ЮНИТИ-ДАНА,200, – 281с.
[1] Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. Учебник для вузов. - М.: ЮНИТИ, 2008,–с. 23.
[2] Кремер Н., Путко Б. Эконометрика.- М.:ЮНИТИ-ДАНА,200, –с.64
[3] Дрейер Н., Смит Г., Прикладной регрессионный анализ. - М.: Финансы и статистика, 2006,– с57.
[4] Практикум по эконометрике/Под ред. И.И.Елисеевой.- М.: Финансы и статистика, 2004, –с 172.
© 2009 База Рефератов