Реферат: Имитационные модели

Реферат: Имитационные модели

Реферат по теме:

Имитационные модели

Введение

Одна из важных особенностей АСУ – принципиальная невозможность проведения реальных экспериментов до завершения проекта. Возможным выходом является использование имитационных моделей. Однако их разработка и использование чрезвычайно сложны, возникают затруднения в достаточно точном определении степени адекватности моделируемому процессу. Поэтому важно принять решение – какую создать модель.

Другой важный аспект использование имитационных моделей в процессе эксплуатации АСУ для принятия решений. Такие модели создаются в процессе проектирования, чтобы их можно было непрерывно модернизировать и корректировать в соответствии с изменяющимися условиями работы пользователя.

Эти же модели могут быть использованы для обучения персонала перед вводом АСУ в эксплуатацию и для проведения деловых игр.

1. Понятие имитационного моделирования

Имитационное моделирование это метод исследования, заключающийся в имитации на ЭВМ с помощью комплекса программ процесса функционирования системы или отдельных ее частей и элементов. Сущность метода имитационного моделирования заключается в разработке таких алгоритмов и программ, которые имитируют поведение системы, ее свойства и характеристики в необходимом для исследования системы составе, объеме и области изменения ее параметров.

Принципиальные возможности метода весьма велики, он позволяет при необходимости исследовать системы любой сложности и назначения с любой степенью детализации. Ограничениями являются лишь мощность используемой ЭВМ и трудоемкость подготовки сложного комплекса программ.

В отличие от математических моделей, представляющих собой аналитические зависимости, которые можно исследовать с помощью достаточно мощного математического аппарата, имитационные модели, как правило, позволяют проводить на них лишь одиночные испытания, аналогично однократному эксперименту на реальном объекте. Поэтому для более полного исследования и получения необходимых зависимостей между параметрами требуются многократные испытания модели, число и продолжительность которых во многом определяются возможностями используемой ЭВМ, а также свойствами самой модели.

Использование имитационных моделей оправдано в тех случаях, когда возможности методов исследования системы с помощью аналитических моделей ограничены, а натурные эксперименты по тем или иным причинам нежелательны или невозможны.

Даже в тех случаях, когда создание аналитической модели для исследования конкретной системы в принципе возможно, имитационное моделирование может оказаться предпочтительным по затратам времени ЭВМ и исследователя на проведение исследования. Для многих задач, возникающих при создании и функционировании АСУ, имитационное моделирование иногда оказывается единственным практически реализуемым методом исследования. Этим в значительной степени объясняется непрерывно возрастающий интерес к имитационному моделированию и расширение класса задач, для решения которых оно применяется.

Методы имитационного моделирования развиваются и используются в основном в трех направлениях: разработка типовых методов и приемов создания имитационных моделей; исследование степени подобия имитационных моделей реальным системам; создание средств автоматизации программирования, ориентированных на создание комплексов программ для имитационных моделей.

Различают два подкласса систем, ориентированных на системное и логическое моделирование. К подклассу системного моделирования относят системы с хорошо развитыми общеалгоритмическими средствами; с широким набором средств описания параллельно выполняемых действий, временных последовательностей выполнения процессов; с возможностями сбора и обработки статистического материала. В таких системах используют специальные языки программирования и моделирования – СИМУЛА, СИМСКРИПТ, GPSS и др. Первые два из этих языков являются подмножествами процедурно-ориентированных языков программирования типа ФОРТРАН, ПЛ/1, расширенными средствами динамических структур данных, операторами управления квазипараллельными процессами, специальными средствами сбора статистики и обработки списков. Эти дополнительные возможности позволяют вести статистические исследования моделей, поэтому такие системы иногда называют системами статистического моделирования.

К подклассу логического моделирования относят системы, позволяющие в удобной и сжатой форме отражать логические и топологические особенности моделируемых объектов, обладающие средствами работы с частями слов, преобразования форматов, записи микропрограмм. К этому подклассу систем относят языки программирования АВТОКОД, ЛОТИС и др.

В большинстве случаев при имитационном моделировании экономических, производственных и других организационных систем управления исследование модели заключается в проведении стохастических экспериментов. Отражая свойства моделируемых объектов, эти модели содержат случайные переменные, описывающие как функционирование самих систем, так и воздействия внешней среды. Поэтому наибольшее распространение получило статистическое моделирование.

Имитационная модель характеризуется наборами входных переменных

наблюдаемых или управляемых переменных

управляющих воздействий

возмущающих воздействий

Состояние системы в любой момент времени

 и начальные условия Y(t0), R(t0), W(t0) могут быть случайными величинами, заданными соответствующим распределением вероятностей. Соотношения модели определяют распределение вероятностей величин в момент t + ∆t:

Существуют два основных способа построения моделирующего алгоритма – принцип ∆t и принцип особых состояний.

Принцип ∆t. Промежуток времени (t0, t), в котором исследуется поведение системы, разбивают на интервалы длиной ∆t. В соответствии с заданным распределением вероятностей для начальных условий по априорным соображениям или случайным образом выбирают для начального момента t0 одно из возможных состояний z0(t0). Для момента t0 + ∆t вычисляется условное распределение вероятностей состояний (при условии состояния z0(t0)). Затем аналогично предыдущему выбирают одно из возможных состояний z0(t0 + ∆t), выполняют процедуры вычисления условного распределения вероятностей состояний для момента t0 + 2∆t и т.д.

В результате повторения этой процедуры до момента t0 + n∆t = T получают одну из возможных реализаций исследуемого случайного процесса. Таким же образом получают ряд других реализаций процесса. Описанный способ построения моделирующего алгоритма занимает много машинного времени.

Принцип особых состояний. Все возможные состояния системы Z(t) = {zi(t)} разбивают на два класса обычные и особые. В обычных состояниях характеристики zi(t) меняются плавно и непрерывно. Особые состояния определяются наличием входных сигналов или выходом, по крайней мере, одной из характеристик zi(t) на границу области существования. При этом состояние системы меняется скачкообразно.

Моделирующий алгоритм должен предусматривать процедуры определения моментов времени, соответствующих особым состояниям, и величин характеристик системы в эти моменты. При известном распределении вероятностей для начальных условий выбирают одно из возможных состояний и по заданным закономерностям изменений характеристик zi(t) находят их величины перед первым особым состоянием. Таким же образом переходят ко всем последующим особым состояниям. Получив одну из возможных реализаций случайного многомерного процесса, с использованием аналогичных процедур строят другие реализации. Затраты машинного времени при использовании моделирующего алгоритма по принципу особых состояний обычно меньше, чем по принципу ∆t.

Имитационное моделирование используют в основном для следующих применений:

1) при исследовании сложных внутренних и внешних взаимодействий динамических систем с целью их оптимизации. Для этого изучают на модели закономерности взаимосвязи переменных, вносят в модель изменения и наблюдают их влияние на поведение системы;

2) для прогнозирования поведения системы в будущем на основе моделирования развития самой системы и ее внешней среды;

3) в целях обучения персонала, которое может быть двух типов: индивидуальное обучение оператора, управляющего некоторым технологическим процессом или устройством, и обучение группы людей, осуществляющих коллективное управление сложным производственным или экономическим объектом.

В системах обоих типов комплекс программ задает некоторую обстановку на объекте, однако между ними имеется существенное различие. В первом случае программное обеспечение имитирует функционирование объектов, описываемых технологическими алгоритмами или передаточными функциями; модель ориентирована на тренировку психофизиологических характеристик человека, поэтому такие модели называются тренажерами. Модели второго типа гораздо сложнее. Они описывают некоторые аспекты функционирования предприятия или фирмы и ориентированы на выдачу некоторых технико-экономических характеристик при воздействии на входы чаще всего не отдельного человека, а группы людей, выполняющих различные функции управления;

4) для макетирования проектируемой системы и соответствующей части управляемого объекта с целью прикидочной проверки предполагаемых проектных решений. Это позволяет в наиболее наглядной и понятной заказчику форме продемонстрировать ему работу будущей системы, что способствует взаимопониманию и согласованию проектных решений. Кроме того, такая модель позволяет выявить и устранить возможные неувязки и ошибки на более ранней стадии проектирования, что на 2–3 порядка снижает стоимость их исправления.

2. Имитационные модели производственных процессов

Вид модели производственного процесса зависит в значительной степени от того, является ли он дискретным или непрерывным. В дискретных моделях переменные изменяются дискретно в определенные моменты имитационного времени. Время может приниматься как непрерывным, так и дискретным в зависимости от того, могут ли дискретные изменения переменных происходить в любой момент имитационного времени или только в определенные моменты. В непрерывных моделях переменные процесса являются непрерывными, а время может быть как непрерывным, так и дискретным в зависимости от того, являются непрерывные переменные доступными в любой момент имитационного времени или только в определенные моменты. В обоих случаях в модели предусматривают блок задания времени, который имитирует продвижение модельного времени, обычно ускоренного относительно реального.

Разработка имитационной модели и проведение моделирующих экспериментов в общем случае могут быть представлены в виде нескольких основных этапов, приведенных на рис. 1.

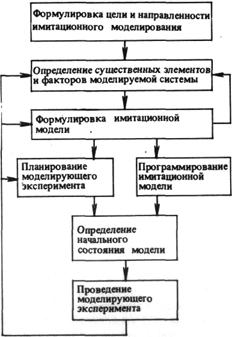
Рис. 1

Компонента модели, отображающая определенный элемент моделируемой системы, описывает набором характеристик количественного или логического типа. В зависимости от длительности существования различают компоненты условно-постоянные и временные. Условно-постоянные компоненты существуют в течение всего времени эксперимента с моделью, а временные – генерируются и уничтожаются в ходе эксперимента. Компоненты имитационной модели делят на классы, внутри которых они имеют одинаковый набор характеристик, но отличаются их значениями.

Состояние компоненты определяется значениями ее характеристик в данный момент модельного времени, а совокупность значений характеристик всех компонент определяет состояние модели в целом.

Изменение значений характеристик, являющееся результатом отображения в модели взаимодействия между элементами моделируемой системы, приводит к изменению состояния модели. Характеристика, значение которой в ходе моделирующего эксперимента изменяется, является переменной, в противном случае это параметр. Значения дискретных переменных не изменяются в течение интервала времени между двумя последовательными особыми состояниями и меняются скачком при переходе от одного состояния к другому.

Моделирующий алгоритм представляет собой описание функциональных взаимодействий между компонентами модели. Для его составления процесс функционирования моделируемой системы разбивается на ряд последовательных событий, каждое из которых отражает изменение состояния системы в результате взаимодействия ее элементов или воздействия на системы внешней среды в виде входных сигналов. Особые состояния возникают в определенные моменты времени, которые планируются заранее, либо определяются в ходе эксперимента с моделью. Наступление событий в модели планируется путем составления расписания событий по временам их свершения либо проводится анализ, выявляющий достижение переменными характеристиками установленных значений.

Для этой цели наиболее удобно использовать СИВС. Представленные на них материальные и информационные потоки легко анализировать для выявления особых состояний. Такими состояниями являются отражаемые на СИВС моменты окончания обработки изделия на каждом рабочем месте или его транспортировки; приема и выдачи на постоянное или временное хранение; сборки деталей в узлы, узлов в изделие и т.п. Для дискретного производства изменение характеристик между особыми состояниями можно также считать дискретным, имея в виду переход условным скачком от исходного материала к заготовке, от заготовки к полуфабрикату, от полуфабриката к детали и т.д.

Таким образом, каждая производственная операция рассматривается как оператор, изменяющий значение характеристик изделия. Для простых моделей последовательность состояний можно принимать детерминированной. Лучше отражают действительность случайные последовательности, которые можно формализовать в виде случайных приращений времени, имеющих заданное распределение, либо случайного потока однородных событий, аналогично потокам заявок в теории массового, обслуживания. Аналогичным образом можно проанализировать и выявить с помощью СИВС особые состояния при движении и обработке информации.

На рис. 2 представлена структура обобщенной имитационной модели.

При моделировании непрерывных производственных процессов по принципу ∆t датчик временных интервалов выдает тактовые импульсы для работы моделирующего алгоритма. Блоки случайных и управляющих воздействий, а также начальных условий служат для ручного ввода условий проведения очередного модельного эксперимента.

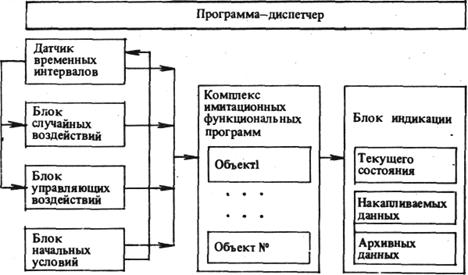
Рис. 2

Комплекс имитационных функциональных программ по каждому моделируемому объекту определяет условное распределение вероятностей состояний объекта к окончанию каждого момента ДЛ При случайном выборе одного из возможных состояний это осуществляется функциональной подпрограммой; при выборе экспериментатором – программой, заложенной в блоке управляющих воздействий, или, при желании осуществлять этот выбор вручную на каждом такте, вводом новых начальных условий исходя из текущего состояния, определяемого с помощью блока индикации.

Функциональная программа определяет параметры технологической установки на каждом такте в зависимости от заданных начальных условий – характеристик сырья, заданного режима, свойств и условий работы установки. Из модели технологической части программным путем могут быть добавлены соотношения весового и объемного баланса.

Координацию и взаимодействие всех блоков и программ осуществляет программа-диспетчер.

При моделировании дискретных процессов, при котором обычно используют принцип особых состояний, структура имитационной модели изменяется незначительно. Вместо датчика временных интервалов вводится блок, определяющий наличие особого состояния и выдающий команду на переход к следующему. Функциональная программа имитирует на каждом переходе одну операцию на каждом рабочем месте. Характеристики таких операций могут быть детерминированными во времени, например при работе станка-автомата, либо случайными с заданными распределениями. Кроме времени могут имитироваться и другие характеристики – наличие или отсутствие брака, отнесение к некоторому сорту или классу и т.п. Аналогично имитируются сборочные операции, с той разницей, что на каждой операции изменяются не характеристики обрабатываемого материала, а вместо одних наименований – детали, узлы – появляются другие узлы, изделия – с новыми характеристиками. Однако принципиально операции сборки имитируются аналогично операциям обработки – определяются случайные или детерминированные затраты времени на операцию, значения физических и производственных характеристик.

3. Имитационные модели предприятий и производственных объединений

Для имитации сложных производственных систем требуется создание логико-математической модели исследуемой системы, позволяющей проведение с нею экспериментов на ЭВМ. Модель реализуют в виде комплекса программ, написанных на одном из универсальных языков программирования высокого уровня либо на специальном языке моделирования. С развитием имитационного моделирования появились системы и языки, сочетающие возможности имитации как непрерывных, так и дискретных систем, что позволяет моделировать сложные системы типа предприятий и производственных объединений.

При построении модели, прежде всего, следует определить ее назначение. В модели должны быть отражены все существенные с точки зрения цели ее построения функции моделируемого объекта и в то же время в ней не должно быть ничего лишнего, иначе она будет слишком громоздкой и мало эффективной.

Основным назначением моделей предприятий и объединений является их исследование с целью совершенствования системы управления либо обучения и повышения квалификации управленческого персонала. При этом моделируется не само производство, а отображение производственного процесса в системе управления.

Для построения модели используется укрупненная СИВС. Методом единичной нити выявляют те функции и задачи, в результате которых может быть получен искомый результат в соответствии с назначением модели. На основании логико-функционального анализа строят структурную схему модели. Построение структурной схемы позволяет выделить ряд самостоятельных моделей, входящих в виде составных частей в модель предприятия. На рис. 3 приведен пример построения структурной схемы моделирования финансово-экономических показателей предприятия. Модель учитывает как внешние факторы – спрос на продукцию, план поставок, так и внутренние – затраты на производство, существующие и планируемые производственные возможности.

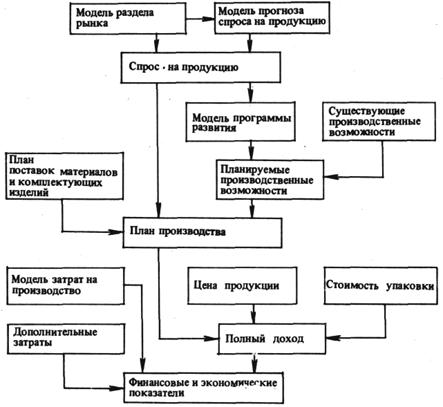
Рис. 3

Некоторые из моделей являются детерминированными – расчет планируемого полного дохода по номенклатуре и количествам в соответствии с планом производства при известных ценах и стоимости упаковки. Модель плана производства является оптимизационной, настраиваемой на один из возможных критериев – максимизацию дохода или использования производственных мощностей; наиболее полное удовлетворение спроса; минимизацию потерь поставляемых материалов и комплектующих изделий и пр. В свою очередь модели спроса на продукцию, планируемых производственных мощностей и плана поставок являются вероятностными с различными законами распределения.

Взаимосвязь между моделями, координация их работы и связь с пользователями осуществляется с помощью специальной программы, которая на рис. 3 не показана. Эффективная работа пользователей с моделью достигается в режиме диалога.

Построение структурной схемы модели не формализовано и во многом зависит от опыта и интуиции ее разработчика. Здесь важно соблюдать общее правило – лучше на первых этапах составления схемы включить в нее большее число элементов с последующим их постепенным сокращением, чем начать с некоторых, кажущихся основными, блоков, намереваясь в последующем их дополнять и детализировать.

После построения схемы, обсуждения ее с заказчиком и корректировки переходят к построению отдельных моделей. Необходимая для этого информация содержится в системных спецификациях перечень и характеристики задач, необходимые для их решения исходные данные и выходные результаты и т д. Если системные спецификации не составлялись, эти сведения берут из материалов обследования, а иногда прибегают к дополнительным обследованиям.

Важнейшими условиями эффективного использования моделей являются проверка их адекватности и достоверность исходных данных. Если проверка адекватности осуществляется известными методами, то достоверность имеет некоторые особенности. Они заключаются в том, что во многих случаях исследование модели и работу с нею лучше проводить не с реальными данными, а со специально подготовленным их набором. При подготовке набора данных руководствуются целью использования модели, выделяя ту ситуацию, которую хотят промоделировать и исследовать.