
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Курсовая работа: Анализ электрического состояния линейных электрических цепей постоянного тока
Курсовая работа: Анализ электрического состояния линейных электрических цепей постоянного тока
Министерство образования Республики Беларусь
Гомельский государственный дорожно-строительный техникум
Специальность 2-400202
Группа ВТ-21
Пояснительная записка
к курсовому проекту
по предмету
“Теоретические основы электротехники”
КП 2-400202.021.022 ПЗ
Выполнил: Лукашевич Алексей Николаевич
Проверил: Авраменко Светлана Прокофьевна
Гомель 2005
Содержание
Введение. 4
1. Анализ электрического состояния линейных электрических цепей постоянного тока. 5
1.1 Составляем на основании законов Кирхгофа системы уравнений для определения токов во всех ветвях схемы.. 5
1.2 Определяем токи во всех ветвях схемы на основе метода контурных токов 6
1.3 Определение токов во всех ветвях схемы на основе метода наложения 8
1.4 Составляем баланс мощностей для заданной схемы.. 12
1.5 Представление результатов расчетов в виде таблицы и их сравнение. 12
1.6 Определение тока во второй ветви методом эквивалентного генератора 12
1.7 Построение потенциальной диаграммы для замкнутого контура, включающего два источника. 14
2 Анализ электрического состояния нелинейных электрических цепей постоянного тока. 15
2.1 Построение ВАХ для заданной схемы (рис.2.0) 15
2.2 Определение на основе ВАХ токов во всех ветвях схемы и напряжений на отдельных элементах. 16
3. Анализ электрического состояния однофазных линейных электрических цепей переменного тока. 17
3.1 Расчет реактивных сопротивлений элементов электрической цепи. 17
3.2 Определение действующих значений токов во всех ветвях электрической цепи 18
3.3 Составление уравнения мгновенного значения тока источника. 18
3.4 Построение векторной диаграммы токов, совмещенной с топографической векторной диаграммой напряжений. 19
4. Анализ электрического состояния трехфазных линейных электрических цепей переменного тока. 20
4.1 Построение схемы замещения электрической цепи соответствующей заданному варианту (рис.4.0) 20
4.2 Расчет реактивных сопротивлений элементов электрической цепи. 20
4.3 Определение действующих значений токов во всех ветвях электрической цепи 21
4.4 Составление уравнения мгновенного значения тока источника. 21
4.5 Составление баланса активных и реактивных мощностей. 21
5. Исследование переходных процессов в электрических цепях. 24
5.1 Определение постоянной времени τи длительности переходного процесса 24
5.2 Определение тока в цепи и энергии электрического (магнитного) поля при t = 3 τи 25
5.3 Построение графиков I=f(t); (Uc=f(t)) 25
Заключение. 27
Введение
Целью данного курсового проекта является формирование у учащегося навыков по решению различных типов задач.
Задача анализа электрического состояния цепей постоянного/переменного тока заключается в определении токов в отдельных ветвях, напряжения между двумя любыми узлами цепи или конкретно на отдельном элементе, а также построение необходимых диаграмм. Расчеты производятся различными методами: по I и II закону Кирхгофа, методом наложения, методом эквивалентного генератора, используется метод расчета электрической цепи с помощью комплексных чисел. При этом задаются: конфигурация и параметры цепи, параметры элементов включенных в цепь, а также параметры источников питания. Если цепь содержит хотя бы один нелинейный элемент, то к ней применяется графический метод решения. Если исследуются переходные процессы в электрической цепи, то необходимо знать начальные значения токов на индуктивностях и напряжения на емкостях.
Работа над данным курсовым проектом позволяет решить следующие задачи:
закрепление теоретических знаний, полученных на лекционном курсе;
развитие творческого технического мышления;
усвоение методики выполнения расчетов;
развитие навыков по работе со справочной литературой;
развитие умения составления и оформления пояснительной записки и графической части проекта;
Курсовое проектирование по предмету “Теоретические основы электротехники” является завершающим этапом изучения данного предмета и занимает важное место в процессе подготовки будущего специалиста к работе на производстве.
1. Анализ электрического состояния линейных электрических цепей постоянного тока
Схема электрической цепи постоянного тока:
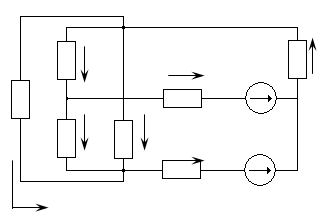
R2 I2 R7
I5 E1,r02 I7
R1
I3 R5
R3 R4 I4 I6
I1 E2,r02
R6
Рис.1.0
Числовые параметры:
E1=30B. r01=3Om. R1=16Om. R3=22Om. R5=43Om R7=55Om.
E2=40B. r02=2Om R2=27Om. R4=33Om. R6=51Om.
1.1 Составляем на основании законов Кирхгофа системы уравнений для определения токов во всех ветвях схемы
![]()
![]() I2-I5-I3=0;
I2-I5-I3=0;
I2-I5-I3=0;
I2-I5-I3=0;
I5+I6-I7=0; I5+I6-I7=0;
I7-I1-I2-I4=0; I7-I1-I2-I4=0;
E2-E1=R3I3-(R5+r01) I5+(R6+r02) I6; 10=53I6-46I5+22I3;
E1=R2I2+(R5+r01) I5+R7I7; 0=55I7+27I2+46I5;
0=R4I4-R3I3-R2I2; 0=33I4-22I3-27I2;
0=I1R1-I4R4; 0=16I1-33I4;
Решив данную систему, мы найдем истинные токи в ветвях.
1.2 Определяем токи во всех ветвях схемы на основе метода контурных токов
Преобразуем схему (рис.1.0) в эквивалентную (рис.1.1):
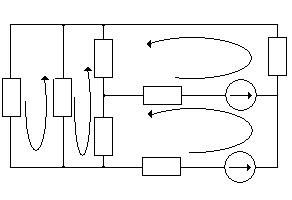
IK3 IK2
IK4 R2 R5 E2,r02 R7
R1 R4
IK1
R3 R6
E1,r01
Рис.1.1
Составляем уравнения для 4-х. контуров:
I-й. Контур:
E2-E1=IK1(R6+r02+r01+R5+R3) +IK2(R5+r01) - IK3R3;
II-й. Контур:
E1= IK2(R5+r01+R7+R2) +IK3R2-IK1(R5+r01);
III-й. Контур:
0=IK3(R4+R3+R2) - IK2R2-IK1R3-IK4R4;
IV-й. Контур:
0=IK4(R1+R4) - IK3R4;
![]() Решаем систему:
Решаем систему:
10=121IK1-46IK2-22IK2;
30=128IK2-27IK3-46IK1;
0=82IK3-27IK2-22IK1-33IK4;
0=49IK4-33IK3;
49IK4-33IK3 => 49IK4=33IK3 => IK4=0,67347IK3;
0=59,77549IK3-27IK2-22IK1;
10=121IK1-46IK2-22IK2;
![]() 30=128IK2-27IK3-46IK1;
30=128IK2-27IK3-46IK1;
0=59,77549IK3-27IK2-22IK1;
IK1=(128IK2-27IK3-30) /46;
10=121((128IK2-27IK3-30) /46) - 46IK2-22IK3 =>
IK2=(93,02174IK3+88,91304) /290,69566;
IK1=(13,95962IK3+9,15046) /46;
0=59,77549IK3-8,63992IK3-8,3583-6,67634IK3-4,37631
12,63461=44,45923IK3 =>
IK3=0,28418 A;
IK4=0, 19139 A;
IK2=0,39680 A;
IK1=0,28516 A;
Вычисляем истинные токи ветвей электрической цепи, выполняя алгебраическое сложение контурных токов, учитывая их направление:
I1=IK4=0, 19139 A.
I2=IK2-IK3=0,11262 A.
I3=IK1-IK3=0,00098 A.
I4=IK3-IK4=0,09279 A.
I5=IK2-IK1=0,11164 A.
I6=IK1=0,28516 A.
I7=IK2= 0,39680 A.
1.3 Определение токов во всех ветвях схемы на основе метода наложения
a) Нахождение частных токов при исключении источника питания Е2:
Преобразовываем схему (рис.1.0) в эквивалентные схемы на (рис.1.2), (рис.1.3) и (рис.1.4) без Е2, оставив лишь его внутреннее сопротивление r02:
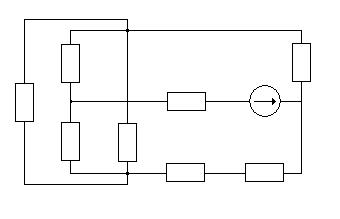
![]()
![]() R2
R7 I/7
R2
R7 I/7
I/2 I/5 E1,r01
![]()
![]() R5
R5
R1 I/1
![]()
![]() R4
R4
![]() R3 I/3 I/4 I/6
R3 I/3 I/4 I/6
R6 r02
Рис.1.2
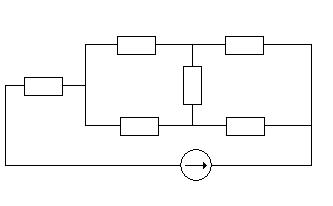
R2 R7
R5
R14
R3 R602
E1, r01
Рис.1.3
R14=(R1R4)/(R1+R4)=(16*33)/(16+33)=10,77551 Om;
R602=R6+r02=51+2=53 Om;
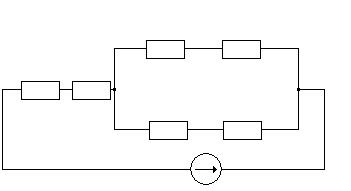
R214 R7
R5 R23
R314 R602
E1,r01
Рис.1.4
R214=(R2R14) /(R2+R3+R14) =(27*10.7755) /(27+10.7755+22) =4,86719 Om;
R23=(R2R3) /(R2+R3+R14) =(27*22) /(27+22+10.7755) =9,93718 Om;
R314=(R3R14) /(R3+R14+R2) =(22*10.7755) /(22+10.7755+27) =3,96586 Om;
R2147=R214+R7= 4.8672+55=59,86719 Om;
R314602=R314+R602= 3.9659+53=56,96586 Om;
RЭКВ. =R5+R23+(R2147R314602) /(R2147+R314602) +r1= =43+9.9372+(59.8672*56.9659) /(59.8672+56.9659) +3=85,12743 Om;
I/=E1/RЭКВ. = 30/85.1275=0,35241 A.
I/5=I/=0,35241 A.
I/7=I/(R314+R602) /(R214+R7+R314+R602) = =0.35241*(3.96586+53) /(4.86719+55+3.96586+53) =0,17182 A.;
I/602=I/6=I/(R214+R7) /(R214+R7+R314+R602) = =0.35241*(9.93718+55) /(9.93718+55+3.96586+53) =0,18058 A.;
По II закону Кирхгофа находим частный ток (I/14):
I/14R14-I/602R602+I/7R7=0;
I/14=(I/602R602-I/7R7) /R14= (0.18058*53-0.17182*55) /10.77551=0,0111 A.;
U14=I/14R14= 0.0111*10.77551=0,11961 B.;
I/1=U14/R1= 0,11961/16=0,00748 A.;
I/4=U14/R4= 0.11961/33=0,00362 A.;
I/2=I/7-I/14= 0,17182-0,0111=0,16072 A.;
I/3=I/1+I/4+I/6= 0,00748+0,00362+0,18058=0, 19168 A.;
b) Нахождение частных токов при исключении источника питания Е1:
Преобразуем схему (рис.1.0) в эквивалентные схемы на (рис.1.5), (рис.1.6) и (рис.1.7) без Е1, оставив лишь его внутреннее сопротивление r01:
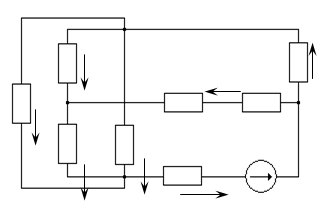
R2
I//5 R7 I//7
R5 r01
R1 I//1
R3 I//3 I//4 I//6
R4
R6 E2,r02
Рис.1.5
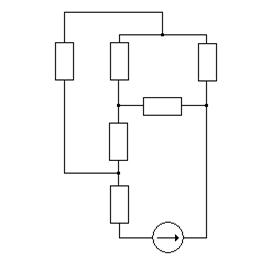
R14 R2 R7
R501
R3
R6 E2,r02
Рис.1.6
R14=(R1R4)/(R1+R4)=(16*33)/(16+33)=10,7755 Om;
R501=R5+r01=43+3=46 Om;
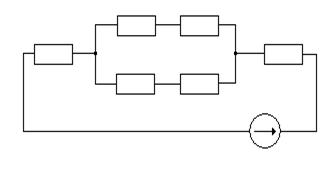 R14 R27
R14 R27
R3 R2501
R6 R751
E2,r02
Рис.1.7
R27=(R2R7)/(R2+R7+R501)=(27*55)/(27+55+46)=11,60156 Om;
R2501=(R2R501)/(R2+R7+R501)=(27*46)/(27+55+46)=9,70313 Om;
R7501=(R7R501)/(R2+R7+R501)=(55*46)/(27+55+46)=19,76563 Om;
R1427=R14+R27=10,7755+11,60156=22,37707 Om;
R32501=R3+R2501=22+9,70313=31,70313 Om;
RЭКВ=R6+R7501+(R1427R32501)/(R1427+R32501)+r02=51+19,76563+(22,37707*31,70313)/
/(22,37707+31,70313)+2=85,8836 Om;
I//=E2/RЭКВ=40/85,8836=0,46575 A.;
I//6=I//=0,46575 A.;
I//14=I//((R3+R2501)/(R14+R27+R3+R2501))=0,46575*((22+9,70313)/ /(10,7755+11,60156+22+9,70313))= 0,27303 A.;
I//3=I//*((R14+R27)/(R14+R27+R3+R2501))=0,46575*((10,7755+11,60156)/ /(10,7755+11,60156+22+9,70313))=0.19272 A.;
U14=I//14*R14=0,27303*10,77551=2,94204 B.;
I//1=U14/R1=2,94204/16=0,18388 A.;
I//4=U14/R4=2,94204/33=0,08915 A.;
По II закону Кирхгофа находим частный ток (I // 5):
E2=I // 6(R6+r02) +I // 5(R5+r01) +I // 3R3;
I // 5=(E2-I // 6(R6+r02) - I // 3R3) /(R5+r01) =(40-0,46575*(51+2) - 0, 19272*22) /(43*3) =
=0,24077 A.;
По I закону Кирхгофа находим частный ток (I // 7 и I // 2):
I // 7=I // 6-I // 5=0,46575-0,24077=0,22498 A.;
I // 2=I // 7-I // 1-I // 4=0,22498-0,18388-0,08915=-0,04805 A.;
Вычисляем токи, текущие в ветвях электрической цепи, выполняя алгебраическое сложение частных токов, учитывая их направление:
I1=I/1+I // 1=0,00748 +0,18388 =0,2151 A.;
I2=I/2-I // 2=0,16072-0,04805=0,11267 A.;
I3=I/3-I // 3=0, 19168-0, 19272=-0,00104 A.;
I4=I/4+I // 4=0,00362+0,08915=0,09277 A.;
I5=I/5-I // 5=0,3524-0,24077=0,11163 A.;
I6=I // 6-I/6=0,46575-0,1877=0,27805 A.;
I7=I/7+I // 7=0,1718+0,22498=0,39678 A.;
1.4 Составляем баланс мощностей для заданной схемы
E1I5+E2I6=I21R1+I22R2+I23R3+I24R4+I25(R5+r01) +I26(R6+r02) +I27R7;
3,88263+10,6064=1,124957+0, 20347+0,03994+0,059915+0,77049+3,726420+8,563179;
14,48903 Вт≈14,48837 Вт;
1.5 Представление результатов расчетов в виде таблицы и их сравнение
| I | Метод контурных токов | Метод наложения | Погрешность |
| I1 | 0, 19139 | 0, 19136 | 0,003% |
| I2 | 0,11262 | 0,11267 | -0,005% |
| I3 | 0,00098 | 0,00104 | -0,006% |
| I4 | 0,09279 | 0,09277 | 0,002% |
| I5 | 0,11164 | 0,11164 | 0% |
| I6 | 0,28516 | 0,28517 | -0,001% |
| I7 | 0,39680 | 0,3968 | 0% |
1.6 Определение тока во второй ветви методом эквивалентного генератора
Удаляем резистор R2 и находим интересующие нас токи электрической цепи в режиме холостого хода (рис.1.8):
I1 I4 IK2 R7 I7
I5
E1,r01
R1 R4
I3
IK3 IK1
R3 I6
R6 E2,rO2
Рис.1.8
Используем метод контурных токов:
Для I контура: E2-E1=IK1(R6+r02+r01+R5+R3)-IK2(R5+r01)-IK3R3;
Для II контура: E1=IK2(R7+R5+r01)-IK1(R5+r01);
Для III контура: 0=Ik3(R4+R3)-IK3R3;
![]() 10=121IK1-46IK2-22IK3;
10=121IK1-46IK2-22IK3;
=101IK2-46IK1;
0=55IK3-22IK1; => IK1=55IK3/22;
10=280,5IK3-46IK2; => IK2=(280,5IK3-10)/46;
30=615,88043IK3-21,95652-115IK3; =>
IK3=0,10391 A.;
IK2=0,41623 A.;
IK1=0,25978 A.;
Истинные токи:
I5=Ik2-I1=0,156455 A.;
I7=IK2=0,41623 A.;
I3=IK1-IK3=0,155865 A.;
I4=IK3=0,10391 A.;
Находим эквивалентное сопротивление данной электрической цепи:
R143=(R1R3R4) /(R1+R3+R4) =11616/71=163,60563 Om.;
R143602=R143+R6+r02=216,60563 Om.;
R143602501=(R143602(R5+r01))
/(R143602+R5+r01) =9963,85898/262,60563=37,94229 Om.;
RЭКВ. =R7+R1-6=92,94229 Om.;
Рассмотрим III контур (рис.1.9):
![]() a
φa=φb+I3R3+I4R4;
a
φa=φb+I3R3+I4R4;
I4 b φa-φb=I3R3+I4R4;
![]() R4 Uab= φa-φb=3,42903+3,42903=6,85806 B.;
R4 Uab= φa-φb=3,42903+3,42903=6,85806 B.;
I3 R3
I2=Uab/R2+RЭКВ=6,85806/119,94229=0,05718 A.;
Рис.1.9
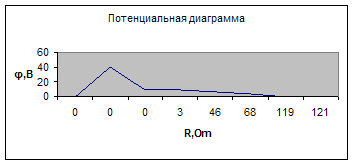
1.7 Построение потенциальной диаграммы для замкнутого контура, включающего два источника
Возьмем контур ABCDEFG (рис.1.10). Обход контура будем проводить против часовой стрелки и заземлим точку А.
I=(E2-E1) /(R5+R3+R6+r01+r02) =10/121=0,08264 A.;
 E R5 D
r01 C E1 B
E R5 D
r01 C E1 B
![]()
R3 I
F R6 G r02 A E2
Рис.1.10
φA=0;
φB=φA+E2=40 B.;
φC=φB-E1=40-30=10 B.;
φD=φC-Ir01=9,75 B.;
φE=φD-IR5=6,2 B.;
φF=φE-IR3=4,4 B.;
φG=φE-IR6=0,2 B.;
φA=φG-Ir02=0 B.;
Потенциальная диаграмма:
2 Анализ электрического состояния нелинейных электрических цепей постоянного тока
2.1 Построение ВАХ для заданной схемы (рис.2.0)
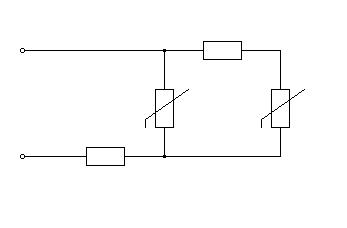
R4
![]() +
+
U HЭ1 НЭ2
R3
-
Рис.2.0
Числовые параметры:
U=200 B.; R3=27 Om.; R4=30 Om.; ВАХ нелинейных элементов (рис.2.1);
I, A
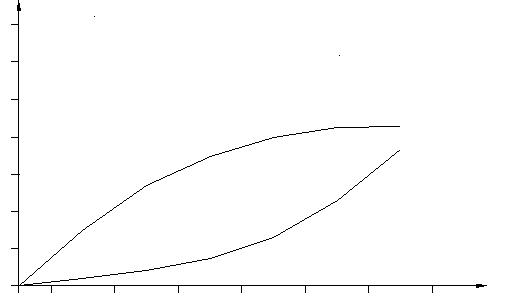 7
7
6
5
НЭ1
4
НЭ2
3
2
1
0
40 80 120 160 200 240 280 U, B
Рис. 2.1
2.2 Определение на основе ВАХ токов во всех ветвях схемы и напряжений на отдельных элементах.
По формуле I=U/R строим ВАХ линейных элементов совмещенной с ВАХ нелинейных элементов (рис.2.2).
I3=U/R3=200/27=7,4 A.;
I4=U/R4=200/30=6,7 A.;
Элементы R4 и НЭ2 соединены последовательно, следовательно строим их результирующую ВАХ (H24) путем алгебраического сложения напряжений при выбранном токе UH4=UHЭ2+UR4;
Элемент Н24 и НЭ1 соединены параллельно, следовательно строим их результирующую ВАХ (H124) путем алгебраического сложения токов при выбранном напряжении IH124=IH24+IHЭ1;
Элементы Н124 и R3 соединены последовательно, следовательно строим их результирующую ВАХ (H1234) таким же образом, что и в первом случае UH1234=UH124+UR3;
С помощью полученной ВАХ H1234 определяем токи в ветвях и напряжения на элементах.
В результате получаем:
3. Анализ электрического состояния однофазных линейных электрических цепей переменного тока
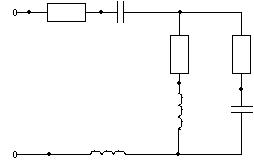 e R1 d C1 a
e R1 d C1 a
+
![]()
R2 R3
~U
c f
L2 C2
-
k L2 b
Рис.3.0
Числовые параметры:
U=Umsin(ωt+ψ) R1=16Om L1=33 mkГн
f=18 kГц R2=30 Om L2=5,1 mkГн
Um=56 B R3=42 Om C1=22 mkФ
ψ=-60 град C2=5,0 mkФ
3.1 Расчет реактивных сопротивлений элементов электрической цепи
XL1=2πfL1=3,7303 Om;
XL2=2πfL2=0,5765 Om;
XC1=1/(2πfC1) =0,4021 Om;
XC2=1/(2πfC2) =1,7693 Om;
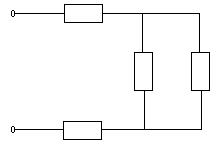
Представим схему (рис.3.0) в виде (рис.3.1):
Z1
![]()
![]()
![]() I1 I3 I4
I1 I3 I4
I2 Z3 Z4
![]() Z2
Z2
Рис.3.1
Находим комплексные сопротивления ветвей, затем участков цепи и всей цепи:
Z1=R1-j XC1=16,0051e-j1,4 Om;
Z2=jXL1=3,7303ej90 Om;
Z3=R2+jXL2=30,0055ej1,1 Om;
Z4=R3-jXC2=42,0373 Om;
Z34=(Z3Z4) /(Z3+Z4) =17,5161-j0,0917=17,5163e-j0,3 Om;
ZЭКВ=Z1+Z34+Z2=33,6720ej5,5 Om;
Нaходим действительное значение напряжения:
Ů=Um/![]() =40e-j60 B;
=40e-j60 B;
3.2 Определение действующих значений токов во всех ветвях электрической цепи
İ=Ů/ZЭКВ=1,1879e-j65,5 A;
İ1=İ2=İ=1,1879e-j65,5 A;
Ů34=İZ34=20,8076e-j65,8 A;
İ3=Ů34/Z3=0,6935e-j66,9 A;
İ4=Ů34/Z4=0,495e-j63,4 A;
3.3 Составление уравнения мгновенного значения тока источника
i=Imsin(ωt+ψ) A;
i=0,01513sin(113043t-65,50) A;
3.4 Составление баланса активных и реактивных мощностей:
Š=Ůİ=47,516ej5,5=47,2972+j4,5542,
где
SИСТ=47,516 ВА (полная мощность источника);
PИСТ=47,2972 Вт (активная мощность источника);
QИСТ=4,5542 Вар (реактивная мощность);
PПР=I21R1+I22R2+I23R3=47,297 Bт;
QПР=I21(-XC1) +I22XL1+I23XL2+I24(-XC2) =4,5402 Вар;
U1=İ1Z1=19,0125e-j66,9 B;
U2=İ2Z2=4,4312e-j24,5 B;
U3=U4=U34=20,8076e-j65,8 B;
Š=Š1+Š2+Š3+Š4=U1I1+U2I2+U3I3+U4I4;
47,2972+j4,5547≈47,2964+j4,5577;
![]()
3.4 Построение векторной диаграммы токов, совмещенной с топографической векторной диаграммой напряжений
Выбираем масштаб:
MI=0,05 A/cм;
MU=1,4 A/см;
Определяем длину вектора по формулам lI=İ/MI и lU=U/MU:
lI=lI1=lI2=23,8 см;
lI3=13,9 см;
lI4=9,9 см;
lU=28,6 см;
lUed=13,6 см;
lUda=0,3 см;
lUac=14,9 см;
lUcb=0,29 см;
lUkb=3,2 см;
lUaf=14,9 см;
lUfb=0,6 см;
4. Анализ электрического состояния трехфазных линейных электрических цепей переменного тока
Схема соединения:
4.1 Построение схемы замещения электрической цепи соответствующей заданному варианту (рис.4.0)
RA XLA
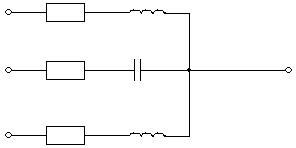
A
RB XCB
0
B
RC XLC
C
Рис.4.0
Числовые параметры:
RA=280 Om; XLA=314 Om; UФ=340 B;
RB=118 Om; XCB=280 Om;
RC=147 Om; XLC=560 Om;
Графоаналитический метод
4.2 Расчет реактивных сопротивлений элементов электрической цепи
![]()
ZA= R2A+X2LA =420,70893 Om;
![]()
ZB= R2B+X2CB =303,84865 Om;
![]()
ZC= R2C+X2LC =578,97237 Om;
cosφA=RA/ZA=0,66554 => φA=480
cosφB=RB/ZB=0,38835 => φB=670
cosφC=RC/ZC=0,25389 => φC=750
4.3 Определение действующих значений токов во всех ветвях электрической цепи
IA=UA/ZA=0,80816 A;
IB=UB/ZB=1,11898 A;
IC=UC/ZC=0,58725 A; c
Определяем ток в нулевом проводе, для этого строим векторную диаграмму.
Под углом 1200 относительно друг друга строятся векторы фазных напряжений одинаковой длинны, векторы же фазных токов строятся в масштабе под углами φ относительно соответствующих фазных напряжений. Если нагрузка носит индуктивный характер, то вектор тока отстает от напряжения на угол φ, если же емкостной, то опережает на угол φ.
MI=0,2 A/см;
Из диаграммы видно, что ток в нулевом проводе равен I0=0,16 A;
4.4 Составление уравнения мгновенного значения тока источника
i=Imsin(ωt+ψ) A; i=
4.5 Составление баланса активных и реактивных мощностей
PA=UIAcosφA=182,87335 Вт;
PB=UIBcosφB=147,749 Bт;
PC=UICcosφC=50,69295 Bт;
PОБЩ=PA+PB+PC=381,3153 Bт;
QA=UIAsinφA=204, 19717 Вар;
QB=UIBsinφB=350, 20901 Вар;
QC=UICsinφC=192,96158 Вар;
QОБЩ=QA+QB+QC=747,26776 Вар;
SA=UIA=247,7744 ВА;
SB=UIB=380,4532 ВА;
SC=UIC=199,665 ВА;
![]()
SОБЩ= P2ОБЩ+Q2ОБЩ = 838,93412 ВА;
Символический метод
Выражаем фазные напряжения в комплексной форме:
UA=UA=340ej0 B;
UB=UB=340e-j120 B;
UC=UC=340e-j240 B;
Выражаем фазные сопротивления в комплексной форме:
ZAejφA=ZA=420,70893ej48 Om;
ZBejφB=ZB=303,84865ej67 Om;
ZCejφC=ZC=578,97237ej75 Om;
Выражаем фазные токи в комплексной форме:
İA=UA/ZA=0,80816e-j48 A;
İB=UB/ZB=1,11898e-j187 A;
İC=UC/ZC=0,58725e-j315 A;
Вычисляем ток в нулевом проводе:
I0=İA+İB+İC=0,16219ej18 A;
Находим активные мощности:
PA=UIAcosφA=182,87335 Вт;
PB=UIBcosφB=147,749 Bт;
PC=UICcosφC=50,69295 Bт;
PОБЩ=PA+PB+PC=381,3153 Bт;
Находим реактивные мощности:
QA=UIAsinφA=204, 19717 Вар;
QB=UIBsinφB=350, 20901 Вар;
QC=UICsinφC=192,96158 Вар;
QОБЩ=QA+QB+QC=747,26776 Вар;
Находим полную мощность цепи:
SA=UAIA=247,7744ej48 BA;
SB=UBIB=380,4532ej67 BA;
SC=UCIC=199,665ej75 BA;
SОБЩ=SA+SB+SC=384, 19197+j747,26777=840,24555ej63 BA;
5. Исследование переходных процессов в электрических цепях
Схема электрической цепи:
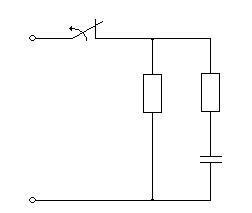 2
2
+ 1
![]()
R1 R2
U
C
-
Рис.5.0
Числовые параметры:
U=220 B;
C=15 мkФ;
R1=106 Om;
R2=106 Om;
Определить:
1. Закон изменения тока и ЭДС в цепи постоянного тока;
2. Длительность переходных процессов (t=5τ);
3. Энергию магнитного поля в момент времени t=3τ;
5.1 Определение постоянной времени τи длительности переходного процесса
Разомкнем переключатель в положение 1. Конденсатор отключается от источника и образуется контур разряда:
τ=(R1R2) /(R1+R2) *C=7,5 c;
uC=uУСТ+uСВ=ue-t/τ;
i=-Ie-t/τ;
Длительность переходного процесса:
t=5τ=5*7,5=37,5 c;
5.2 Определение тока в цепи и энергии электрического (магнитного) поля при t = 3 τи
Определяем ток в цепи в момент времени t = 3 τи:
i=-Ie-t/τ=-1,09 мкА;
Определяем энергию электрического поля конденсатора в момент времени t = 3 τи:
WЭ=C*uC32/2= 0,00089 Дж;
5.3 Построение графиков I=f(t); (Uc=f(t))
Вычисляем значения напряжений на конденсаторе в различные моменты времени по формуле: uC=ue-t/τ;
Изменение напряжения на
конденсаторе при его разрядке (рис.5.1)
| t,c | 0 | τ | 2τ | 3τ | 4τ | 5τ |
| u,B | 220 | 80,9 | 29,8 | 10,9 | 4,03 | 1,5 |
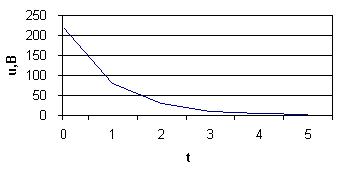
Рис.5.1
Изменение тока на конденсаторе при его разрядке (рис.5.2)
| t,c | 0 | τ | 2τ | 3τ | 4τ | 5τ |
| i, мкА | -110 | -42,98 | -8,046 | -1,09 | -0,1612 | -0,021 |
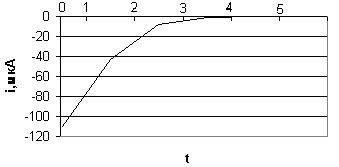
Рис.5.2
Заключение
В данном курсовом проекте я проводил:
анализ электрического состояния линейных электрических цепей постоянного тока
анализ электрического состояния нелинейных электрических цепей постоянного тока
анализ электрического состояния однофазных нелинейных электрических цепей переменного тока
анализ электрического состояния трехфазных нелинейных электрических цепей переменного тока
исследование переходных процессов в электрических цепях
© 2009 База Рефератов