
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Курсовая работа: Анализ сложных электрических цепей постоянного тока и однофазного переменного тока
Курсовая работа: Анализ сложных электрических цепей постоянного тока и однофазного переменного тока
Министерство высшего и профессионального образования
Российской Федерации
Иркутский Государственный Технический Университет
Курсовая работа
По электротехнике и электронике
Анализ сложных электрических цепей постоянного тока и однофазного переменного тока
Выполнил:
Проверила:
Василевич М.Р.
Иркутск 2006г
Содержание:
1. Анализ электрических цепей постоянного тока
Расчёт токов с помощью законов Кирхгофа
Расчёт токов методом контурных токов
Расчёт токов методом узлового напряжения
Исходная таблица расчётов токов
Потенциальная диаграмма для контура с двумя Э.Д.С
Баланс мощности
Определение показания вольтметра
2. Анализ электрических цепей переменного тока
Расчёт токов с помощью законов Кирхгофа
Расчёт токов методом контурных токов
Расчёт токов методом узлового напряжения
Исходная таблица расчётов токов
Векторная диаграмма токов и топографическая диаграмма напряжений на комплексной плоскости
Определение показания вольтметра
1. Анализ электрических цепей постоянного тока
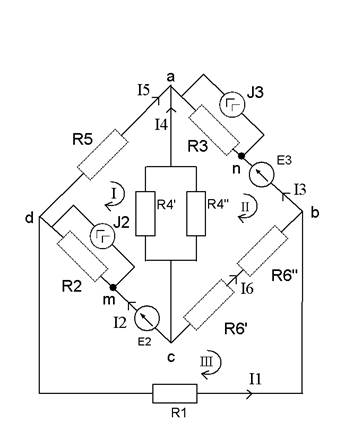
![]() =9 Ом
=9 Ом
![]() =7,5 Ом
=7,5 Ом
![]() =12 Ом
=12 Ом
![]() =22,5 Ом
=22,5 Ом
![]() =315 Ом
=315 Ом
![]() =10,5 Ом
=10,5 Ом
![]() =0
=0
![]() =12 Ом
=12 Ом
![]() =-
=-
![]() =15 В
=15 В
![]() =33 В
=33 В
![]() =-
=-
![]() =2 В
=2 В
![]() =0 В
=0 В
В предложенной электрической цепи заменяем источники тока на источники ЭДС.
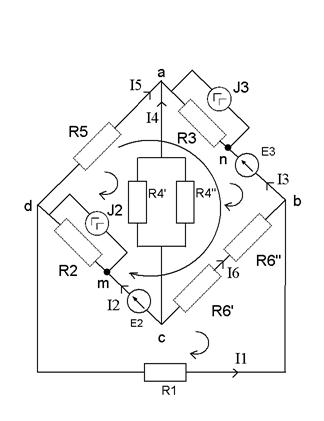 2)Выбираем
условно положительное направление токов.
2)Выбираем
условно положительное направление токов.
3)Выбираем направление обхода независимых контуров.
Находим эквиваленты:
![]() =
=![]() *
*![]() / (
/ (![]() +
+![]() ) =
) =![]() 21
21
![]() =
=![]() +
+![]() =0+12=12 Ом
=0+12=12 Ом
![]() =
=![]() +
+![]() =15+2=17
=15+2=17
![]() =
=![]() +
+![]() =33+0=33
=33+0=33
1.1 Расчёт токов с помощью законов Кирхгофа
Записываем систему уравнений для расчета электрических цепей с помощью законов Кирхгофа. По 1 закону составляем (у-1) уравнение, где у количество узлов. По 2 закону Кирхгофа составляем [b-(y-1)] уравнение, где b – количество ветвей.
a) ![]() +
+![]() +
+![]() =0
=0
b) ![]() -
-![]() +
+![]() =0
=0
c)- ![]() -
-![]() -
-![]() =0
=0
I) ![]()
![]() -
-![]()
![]() +
+![]()
![]() =
=![]()
II) ![]()
![]() -
-![]()
![]() -
-![]()
![]() =-
=-![]()
III)- ![]()
![]() +
+ ![]()
![]() -
-![]()
![]() =-
=-![]()
Рассчитываем систему
уравнений с помощью ЭВМ, векторы решения находятся в приложении 1.
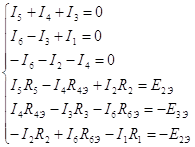
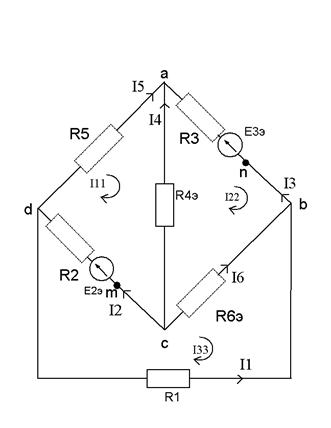
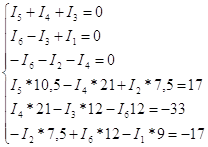
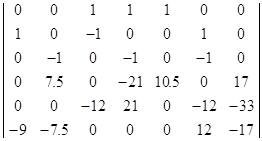
(Данные расчета находятся в приложении 1)
После расчета на ЭВМ записываем:
![]() =1.29 A
=1.29 A ![]() =-0.80 A
=-0.80 A
![]() =0.77 A
=0.77 A ![]() =-0.52 A
=-0.52 A
![]() =1.32 A
=1.32 A ![]() =0.03 A
=0.03 A
1.2 Расчёт токов методом контурных токов
Находим действующие в цепи токи с помощью метода контурных токов. Предполагается, что каждый контурный ток имеет свое собственное контурное сопротивление, которое равно арифметической сумме всех сопротивлений входящих в контур. Контурное ЭДС равно сумме всех ЭДС входящих в контур.
В каждом независимом контуре рассматривают независимые и граничащие ветви. В каждой граничащей ветви находят общее сопротивление, которое равно сопротивлению этой ветви. Составляют систему уравнений, количество которых равно количеству контурных токов. В результате расчета находят контурные токи и переходят к действующим.
1) Предположим, что в
каждом независимом контуре течет свой контурный ток ![]() ,
,![]() ,
,![]() . Выберем произвольно
положительное направление обхода токов в одно направление.
. Выберем произвольно
положительное направление обхода токов в одно направление.
2)Находим полно контурное сопротивление всех контурных токов.
![]() =
=![]() +
+![]() +
+![]() =7,5+10,5+21=39
Ом
=7,5+10,5+21=39
Ом
![]() =
=![]() +
+![]() +
+![]() =21+12+12=45
Ом
=21+12+12=45
Ом
![]() =
=![]() +
+![]() +
+![]() =9+7,5+12=28,5
Ом
=9+7,5+12=28,5
Ом
Находим общее сопротивление
![]() =
=![]() =
=![]()
![]() =
=![]() =
=![]()
![]() =
=![]() =
=![]()
Находим полные контурные ЭДС
![]() =
=![]()
![]() =
=![]()
![]() =-
=-![]()
Составляем систему уравнений для нахождения контурных токов
Согласно второму закону Кирхгофа
![]()
![]() -
-![]()
![]() -
-![]()
![]() =
=![]()
-![]()
![]() +
+![]()
![]() -
-![]()
![]() =
=![]()
-![]()
![]() -
-![]()
![]() +
+![]()
![]() =
=![]()
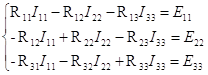
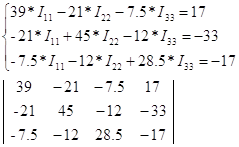
(Данные расчета находятся в приложении 2)
После расчета на ЭВМ записываем:
![]() =-0.52455258749889799877 (А)
=-0.52455258749889799877 (А)
![]() =-1.3224896411883981310 (А)
=-1.3224896411883981310 (А)
![]() =-1.2913691263334214934 (А)
=-1.2913691263334214934 (А)
4.Ток в независимой цепи равен контурному току с учетом знаков, а ток в зависимой цепи равен алгебраической сумме.
![]() =-I33=1.29 A
=-I33=1.29 A
![]() =I11-I33=-0.52455258749889799877-(-1.2913691263334214934)
=0,77 A
=I11-I33=-0.52455258749889799877-(-1.2913691263334214934)
=0,77 A
![]() =-I22=1.32 A
=-I22=1.32 A
![]() =I22-I11=-1.3224896411883981310-(-0.52455258749889799877)
-0,8 A
=I22-I11=-1.3224896411883981310-(-0.52455258749889799877)
-0,8 A
![]() =I11=-0.52 A
=I11=-0.52 A
![]() =I33-I22=-1.2913691263334214934-(-1.3224896411883981310)
=0,03 A
=I33-I22=-1.2913691263334214934-(-1.3224896411883981310)
=0,03 A
В результате токи равны:
![]() =1.29 A
=1.29 A
![]() =0,77 A
=0,77 A
![]() =1.32 A
=1.32 A
![]() = -0,8 A
= -0,8 A
![]() = -0.52 A
= -0.52 A
![]() = 0,03 A
= 0,03 A
1.3 Расчёт токов методом узлового напряжения
Проверяем правильность нахождения токов в заданной электрической цепи методом узловых потенциалов. Согласно этому методу предполагается, что в каждом узле схемы имеется свой узловой ток который равен алгебраической сумме всех токов за счет проводимости ветвей. Этот метод основан на первом законе Кирхгофа и законе Ома.
Заземляем узел 3, φ3=0
Если в электрической схеме заземляется один из узлов, потенциал этой точки равен 0, а тока распределение не меняется.
Находим собственные проводимости ветвей присоединенных к оставшимся узлам 1,2,4. Собственная проводимость ветвей равна арифметической сумме проводимостей ветвей присоединенных к соответствующим узлам.
![]()
![]()
![]()
![]()
![]()
![]()
Находим взаимные проводимости, которые равны проводимости общих ветвей между соседними узлами.
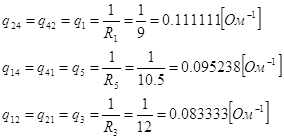
Находим полный узловой ток, который равен сумме произведений ЭДС на соответствующую проводимость.
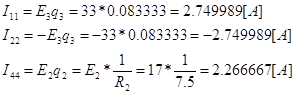
Составляем уравнение в соответствии с первым законом Кирхгофа.
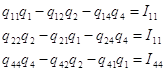
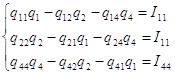
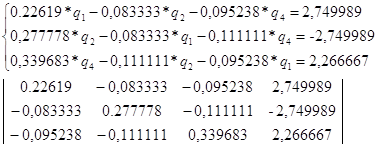
(Данные расчета находятся в приложении 3)
После расчета на ЭВМ записываем:
![]() =16,756645482734525139
=16,756645482734525139 ![]()
![]() -0,37345273475483642976
-0,37345273475483642976 ![]()
![]() 11,248845822938816704
11,248845822938816704 ![]()
1. По закону Ома находим искомые токи.
![]() =(
=(![]() -
-![]() )/
)/![]() =(11,248845822938816704-( -0,37345273475483642976))/9=1,291367
A
=(11,248845822938816704-( -0,37345273475483642976))/9=1,291367
A
![]() =(
=(![]() -
-![]() +
+![]() )/
)/![]() =((0,083333-11,248845822938816704)+17)/7,5=0,777932
A
=((0,083333-11,248845822938816704)+17)/7,5=0,777932
A
![]() =(
=(![]() -
-![]() +
+![]() )/
)/![]() =(0-,37345273475483642976-16,756645482734525139+33)/12=
1,322492 A
=(0-,37345273475483642976-16,756645482734525139+33)/12=
1,322492 A
![]() =(
=(![]() -
-![]() )/
)/![]() =(0,083333-16,756645482734525139)/21=-0,79397 A
=(0,083333-16,756645482734525139)/21=-0,79397 A
![]() =(
=(![]() -
-![]() )/
)/![]() =(11,248845822938816704-16,756645482734525139)/10,5=-0,52455 A
=(11,248845822938816704-16,756645482734525139)/10,5=-0,52455 A
![]() =(
=(![]() -
-![]() )/
)/![]() =(0,083333-( -0,37345273475483642976))/12=0,038065
A
=(0,083333-( -0,37345273475483642976))/12=0,038065
A
Округляем искомые токи до сотых долей:
![]() =1,29
A
=1,29
A
![]() =0,78
A
=0,78
A
![]() =1,32
A
=1,32
A
![]() =-0,79 A
=-0,79 A
![]() =-0,52 A
=-0,52 A
![]() =0,04
A
=0,04
A
1.4 Исходная таблица расчётов токов
V Составляем исходную таблицу расчетов токов всеми методами
|
I токи Метод |
I1,A | I2,A | I3,A | I4,A | I5,A | I6,A |
| Закон Кирхгофа | 1,29 | 0,77 | 1,32 | -0,8 | -0,52 | 0,03 |
| Контурных Токов | 1,29 | 0,77 | 1,32 | -0,8 | -0,52 | 0,03 |
| Узловых Потенциалов | 1,29 | 0,78 | 1,32 | -0,79 | -0,52 | 0,04 |
1.5 Потенциальная диаграмма для контура с двумя Э.Д.С
VI Строим потенциальную диаграмму

∑R=![]() =42 Ом
=42 Ом
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.6Определение показания вольтметра
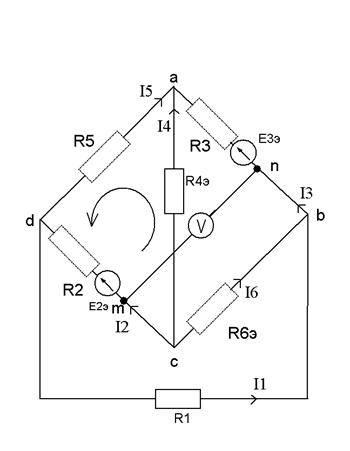
VII Находим показания вольтметра по второму закону Кирхгофа
![]()
pV=![]() -17+33+0,77*7.5+(-0,52)*10.5-1,32*12=
-17+33+0,77*7.5+(-0,52)*10.5-1,32*12=
=0.475 В
1.7 Баланс мощности
XIII Составляем баланс мощности
![]()
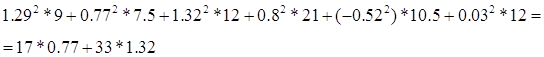
56.62Вт=56.65Вт
2. Анализ электрических цепей переменного тока
1) Начертим электрическую цепь без ваттметра и записать данные.
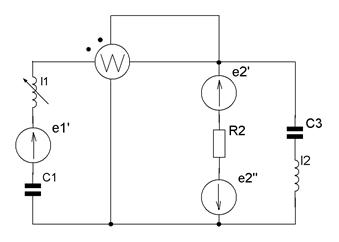
![]() =40.5 мГн
=40.5 мГн
![]() =0 мГн
=0 мГн
![]() =35.4 мкФ
=35.4 мкФ
![]() =53 мкФ
=53 мкФ
![]() =25 Ом
=25 Ом
f=150 Гц
![]() =70.5 cos(ωt+275)
=70.5 cos(ωt+275)
![]() ’=68.5 cos(ωt-174)
’=68.5 cos(ωt-174)
![]() ’=56 sin(ωt-170)
’=56 sin(ωt-170)
2)Найдем сопротивление
элементов входящих в цепь.
![]()
![]() Ом
Ом
![]()
![]() Ом
Ом
![]()
![]() Ом
Ом
![]()
![]() Ом
Ом
3) Находим комплексы ЭДС, входящие в цепь.
Ė= Ė’+ Ė’’
![]()
![]()
![]()
![]() 70.5 В
70.5 В
![]() 68.5 В
68.5 В
![]() =56 В
=56 В
![]()
![]()
![]()
![]()
2.1 Расчёт токов с помощью законов Кирхгофа
4)Производим расчет предложенной схемы методом законов Кирхгофа.
Выбираем условно положительное направление токов. Рассчитываем искомые токи.
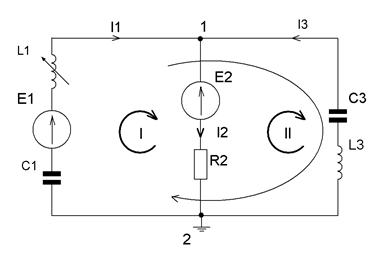
Записываем систему уравнений для мгновенных значений токов и напряжений в соответствии с первым и вторым законами Кирхгофа в интегро-дифференциальной форме, причем по первому закону Кирхгофа составляем (у-1) –уравнений, а по второму закону Кирхгофа –[b-(y-1)]-уравнений.
(у-1)=1
[b-(y-1)]=2
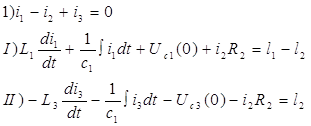
Или в комплексной форме:
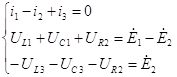
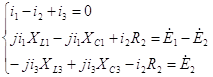
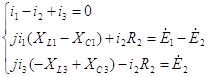
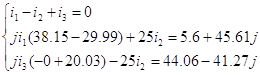
Решаем данную систему уравнений с помощью ЭВМ.
(Данные расчета находятся в приложении 4)
После расчета на ЭВМ записываем значения комплексных токов:
![]() [A]
[A]
![]() [A]
[A]
![]() =
=![]() =4.69
[A]
=4.69
[A]
Находим действующие значения токов:
![]()
![]() =6.37 [A]
=6.37 [A]
![]()
![]() =2.2 [A]
=2.2 [A]
![]()
![]() =4.69 [A]
=4.69 [A]
2.2 Расчёт токов методом контурных токов
5. Производим расчет данной схемы методом контурных токов.
Находим полные контурные сопротивления:
![]() j(38.15-29.99)+25=25+8.16j [Ом]
j(38.15-29.99)+25=25+8.16j [Ом]
![]() j(0-20.03)+25=25-20.03j [Ом]
j(0-20.03)+25=25-20.03j [Ом]
Находим взаимное сопротивление:
![]()
![]()
![]() =25 [Ом]
=25 [Ом]
Находим комплексы полных контурных ЭДС:
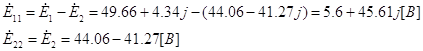
Записываем систему уравнений:
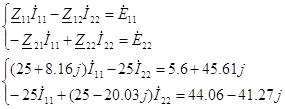
Решаем систему уравнений с помощью ЭВМ.
(Данные расчета находятся в приложении 5)
После расчета на ЭВМ Записываем значения контурных токов:
![]() =3.08+5.57j [A]
=3.08+5.57j [A]
![]() =1.04+4.75j [A]
=1.04+4.75j [A]
Причем контурный ток ![]() равен току в независимой
ветви, т.е. току
равен току в независимой
ветви, т.е. току ![]() . Контурный ток
. Контурный ток ![]() равен току
равен току ![]() в независимой ветви, но
направлен навстречу. Искомый ток
в независимой ветви, но
направлен навстречу. Искомый ток ![]() =
=![]() -
-![]() .
.
Таким образом:
![]() =3.08+5.57j [A]
=3.08+5.57j [A]
![]() =0.24+0.82j [A]
=0.24+0.82j [A]
![]() =-1.04-4.75j [A]
=-1.04-4.75j [A]
2.3Расчёт токов методом узлового напряжения
6) Проверяем правильность нахождения расчета методом узловых потенциалов.
Для этого узел 2 заземляем, а для остальных составляем систему уравнений.
φ2=0
Находим полную комплексную проводимость узла.
![]() =
=![]() 0.04-0.07j
0.04-0.07j ![]()
(Данные расчета находятся в приложении 6)
Находим комплекс узлового тока.
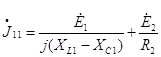 =
=
=![]()
![]()
(Данные расчета находятся в приложении 7)
Находим комплексный потенциал:
![]()
В результате решения этого уравнения находим комплекс потенциала
![]() и по закону Ома находим искомые
токи.
и по закону Ома находим искомые
токи.
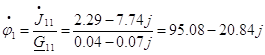
(Данные расчета находятся в приложении 8)
По закону Ома находим искомые токи:
![]() =
=![]() [A]
[A]
(Данные расчета находятся в приложении 9)
![]() =
=![]() [A]
[A]
(Данные расчета находятся в приложении 10)
![]() =
=![]() [A]
[A]
(Данные расчета находятся в приложении 11)
2.4 Исходная таблица расчётов токов
7)Составляем сводную таблицу искомых токов:
|
токи Метод |
|
|
|
| Законы Кирхгофа | 3,08+5,57j | 2.04+0.82j | -1.04-4.75j |
| Контурных Токов | 3,08+5,57j | 2.04+0.82j | -1.04-4.75j |
| Узловых Потенциалов | 3,08+5,57j | 2.04+0.82j | -1.04-4.75j |
2.5 Векторная диаграмма токов и топографическая диаграмма напряжений на комплексной плоскости
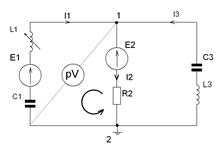
8) Строим на комплексной плоскости векторную диаграмму токов и топографическую диаграмму напряжений и график изменения тока в неразветвленной части цепи.
1.
![]() [B]
[B]
![]() [B]
[B]
2.
![]() [B]
[B]
3.
![]() [B]
[B]
4.
![]() [B]
[B]
![]() =
=![]()
![]() =3.08+5.57j=6.36
=3.08+5.57j=6.36![]() [A]
[A]
![]() =
=![]() [A]
[A]
![]() рад
рад
![]()
(Данные расчета находятся в приложении 12)
2.6 Определение показания вольтметра
9)Определяем показания вольтметра по второму закону Кирхгофа:
pV-![]()
![]()
pV=![]() +
+![]()
![]() =44.06-41.27j+(2.04+0.82j)*25=95.06-20.77j
=44.06-41.27j+(2.04+0.82j)*25=95.06-20.77j
pV=![]() =97 B
=97 B
Приложения
Приложение 1:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
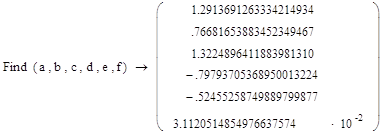
Приложение 2:
![]()
![]()
![]()
![]()
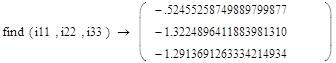
Приложение 3:
![]()
![]()
![]()
![]()
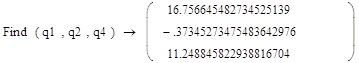
Приложение 4:
![]()
![]()
![]()
![]()
![]()
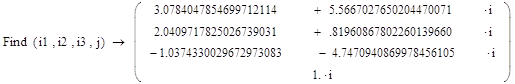
Приложение 5:
![]()
![]()
![]()
![]()
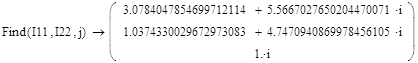
Приложение 6:
![]()
![]()
![]()
![]()
Приложение 7:
![]()
![]()
![]()
![]()
Приложение 8:
![]()
![]()
![]()
![]()
Приложение 9:
![]()
![]()
![]()
![]()
Приложение 10:
![]()
![]()
![]()
![]()
Приложение 11:
![]()
![]()
![]()
![]()
Приложение 12:
График изменения тока в
неразветвленной части цепи 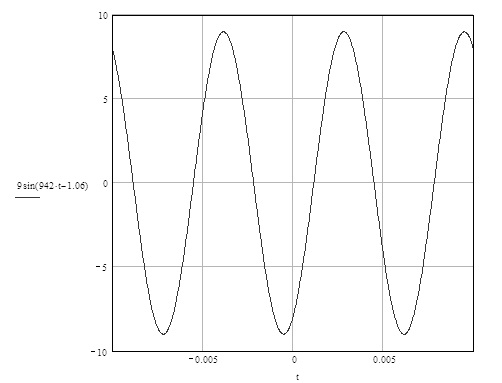
© 2009 База Рефератов