Курсовая работа: Методы расчета линейных электрических цепей при импульсном воздействии. Спектральный анализ сигналов

Курсовая работа: Методы расчета линейных электрических цепей при импульсном воздействии. Спектральный анализ сигналов

ГОСУДАРСТВЕННЫЙ КОМИТЕТ РФ ПО РЫБОЛОВСТВУ

МУРМАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра электрооборудования судов

Пояснительная записка

к курсовой работе по курсу "Основы теории цепей"

Тема: "Методы расчета линейных электрических цепей при импульсном воздействии. Спектральный анализ сигналов"

Мурманск

2009

Оглавление

Формулировка задачи

Качественный анализ переходного процесса

Расчет переходного процесса классическим методом

Расчет переходного процесса операторным методом

Построение графика изменения искомой величины

Составление передаточной функции между заданными переменными

Составление переходной функции

Расчет закона изменения искомой величины при подаче на вход цепи импульса заданной формы

Расчет и построение графика спектральной плотности прямоугольного импульса

Расчет и построение графика спектральной плотности искомой переменной

Список использованной литературы

Формулировка задачи

1.     Выполнить качественный анализ переходных процессов напряжений и токов на реактивных элементах. Построить необходимые графики.

2.     Определить закон изменения во времени тока или напряжения после коммутации, используя классический метод расчета.

3.     Определить закон изменения во времени тока или напряжения после коммутации, используя операторный метод расчета.

4.     На основании полученного аналитического выражения построить график изменения искомой величины во времени в интервале от 0 до , где ,  - наименьший по модулю корень характеристического уравнения.

5.     Записать выражение передаточной функции между искомой величиной и входным напряжением.

6.     Используя выражение передаточной функции, записать выражение соответствующей ей переходной функции.

7.     Рассчитать закон изменения искомой величины при подаче на вход цепи импульса заданной формы.

8.     Рассчитать и построить график спектральной плотности амплитуд одиночного прямоугольного импульса с амплитудой E, длительностью tи=0.2 мс в диапазоне частот, в котором сосредоточено 90℅ энергии этого сигнала.

9.     Рассчитать и построить график спектральной плотности амплитуд искомой величины при подаче на вход цепи одиночного прямоугольного импульса, используя результаты пп. 5 и8. Построение произвести в том же диапазоне и на тех же частотах.

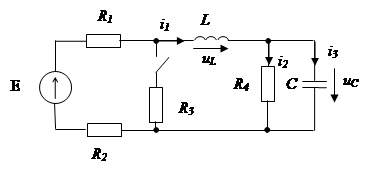
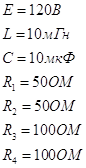
Определить .

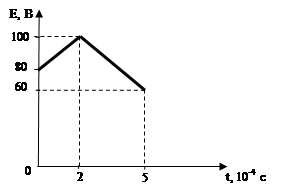
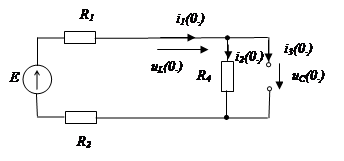
Качественный анализ переходного процесса

Качественный анализ переходного процесса представляет собой метод грубой инженерной оценки. Он заключается в нахождении искомых переменных в определенные моменты времени, в частности, перед коммутацией, в момент коммутации и в установившемся режиме.

1.                Расчет токов и напряжений до коммутации ().

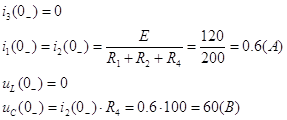
2.                Расчет токов и напряжений в момент коммутации ().

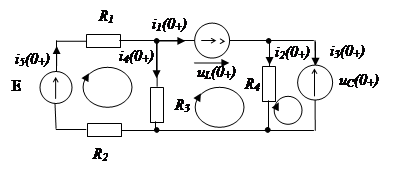
Первый закон коммутации: ток в индуктивности в момент коммутации не может изменятся мгновенно, он остается таким же, каким был непосредственно перед коммутацией, а затем плавно изменяется. Поэтому можно записать, что .

Второй закон коммутации: напряжение на емкости в момент коммутации не может изменятся скачком. Оно остается таким же, каким было перед коммутацией, а затем плавно изменяется. Таким образом .

Для того, чтобы составить систему уравнений Кирхгофа, построим дерево графа цепи. Граф – это изображение электрический цепи без элементов.

Источник тока и источник ЭДС, обозначающие в момент коммутации индуктивность и емкость соответственно, могут не являться идеальными, и иметь конечные значения сопротивлений, поэтому отображаются в графе ребрами.

Таким образом по первому закону Кирхгофа необходимо составить 2 уравнения, а по второму – 3 уравнения.

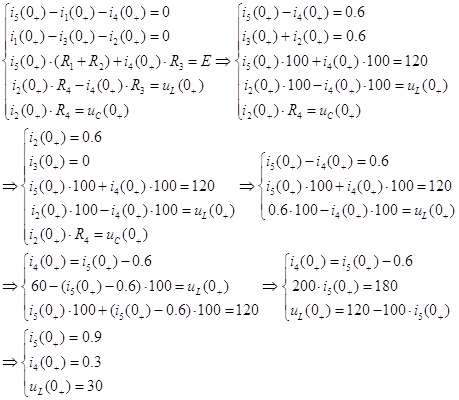
Таким образом получаем

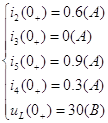
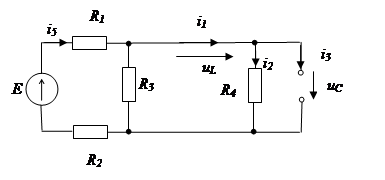
3.                Расчет токов и напряжений в установившемся режиме ().

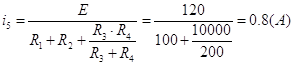
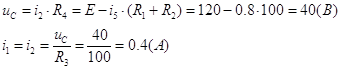
4.                Построение графиков переходного процесса.

Точки А соответствуют значениям переменных в момент до коммутации (). Эти значения были рассчитаны в пункте 1. Точки В соответствуют значениям в момент коммутации (). Это было найдено в пункте 2. Точки С и проходящие через них прямые соответствуют значениям токов и напряжений в установившемся режиме (), что было вычислено в пункте 3.

Линии ВС проведены приблизительно в предположении, что во время переходного процесса токи и напряжения принимают большие значения, чем в установившемся режиме.

Расчет переходного процесса классическим методом

При расчете переходного процесса классическим методом он представляется в виде двух накладывающихся друг на друга процессов: принужденного (который соответствует новому установившемуся режиму) и свободного, затухающего (который существует во время переходного процесса). Благодаря затуханию переходной ток все время приближается к принужденному току.

Так как переходной процесс длится от момента коммутации , до момента установления , то физически реальной является только свободная составляющая.

Вид функции  зависит от формы ЭДС или тока источника и характеризуется структурой цепи и ее элементной базой. Вид функции  зависит только от характера цепи (структуры и элементной базы).

Функция  рассчитывается в схеме после коммутации (ключ в рабочем положении). Вид  определяется корнями характеристического уравнения, которое может быть составлено, например, по входному сопротивлению цепи. То есть в цепи выбирается ветвь без источника тока, в этой ветви делается разрыв, из цепи исключаются все источники и со стороны разрыва записывается уравнение для входного сопротивления . Далее в этом сопротивлении  заменяют на p и приравнивают к нулю.

1.                Составление характеристического уравнения.

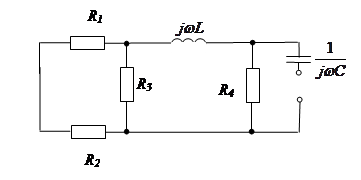
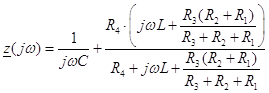
Характеристическое уравнение:

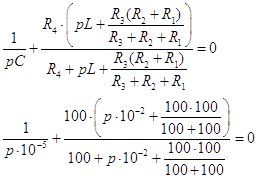
Так как  при любом p, то

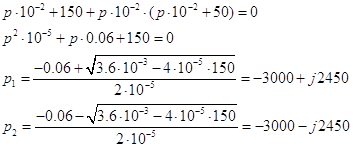
2.                Напряжение .

Так как полученные корни характеристического уравнения являются комплексными сопряженными, то  представляет собой затухающий колебательный процесс и ищется как функция вида , где A и ψ – постоянные интегрирования, а δ – декремент затухания. Все эти константы находятся из следующих условий:

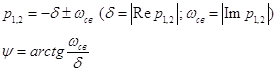
Тогда

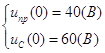 (рассчитано при проведении качественного анализа)

Так как , то . Решая это уравнение, получим значение константы А:

В результате получаем формулу для переходного напряжения на конденсаторе:

Расчет переходного процесса операторным методом

Суть операторного метода заключается в том, что каждому числу из области функций действительной переменной t ставится во взаимнооднозначное соответствие с помощью операторного отображения по Лапласу некоторое число в области функций комплексной переменной частоты ω. В дифференциальное уравнение или интегро-дифференциальное уравнения функции времени заменяется алгебраическим уравнением в функции частоты.

Операции в области отображений осуществляются с помощью простых алгебраических преобразований, а полученные результаты и помощью отображения Лапласа переводятся в область функций времени.

Отображением по Лапласу называется функция, которая получается в результате следующего интегрирования:

, где

Операторная схема замещения индуктивности содержит операторное сопротивление pL и источник ЭДС . Направление источника совпадает с направлением тока в цепи.

Операторная схема замещения емкости содержит операторное сопротивление  и источник ЭДС , напряжение которого противоположно исходному напряжению на емкости.

Все источники заменяются своими операторными отображениями.

Сделав все необходимые преобразования, получаем

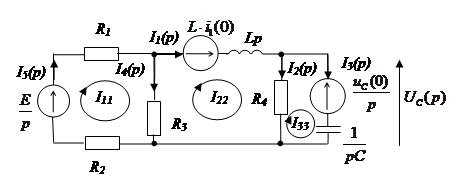
Дерево графа цепи:

Составим систему из трех уравнений по методу контурных токов:

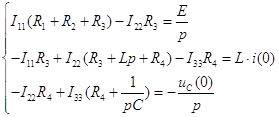
Решим эту систему:

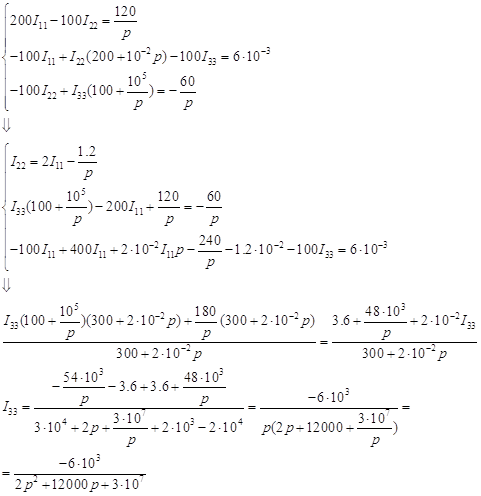
Так как , а , то

Теперь необходимо найти оригинал данного отображения. Из таблиц преобразования по Лапласу известно, что  ([2] стр. 255), поэтому главная сложность заключается в нахождении оригинала второго слагаемого.

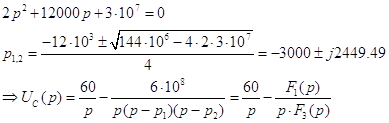
Чтобы найти оригинал второго слагаемого, воспользуемся теоремой разложения Хевисайда: ели изображение имеет вид рациональной дроби, то оригинал определяется в зависимости от корней знаменателя. Так как в данном случае два корня комплексные сопряженные, а третий равен 0, то

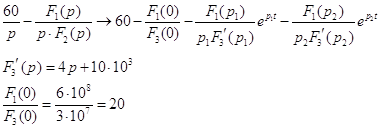
В результате получаем формулу для переходного напряжения на конденсаторе:

Построение графика изменения искомой величины

По правилу пяти τ переходной процесс можно считать завершенным спустя время, равное  после коммутации. Здесь τ - постоянная времени цепи, она определяет скорость затухания процесса, и чем выше τ, тем медленнее идет процесс.

В данной задаче

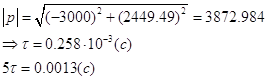
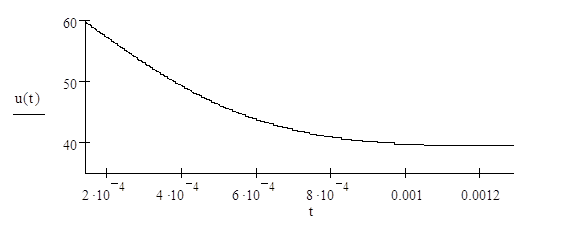
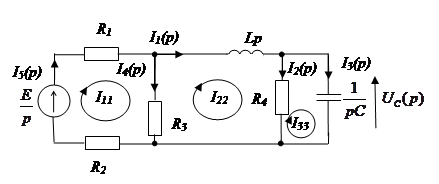
Составление передаточной функции между заданными переменными

Передаточной функцией по напряжению называется отношение изображения по Лапласу выходной функции  к изображению по Лапласу входной функции  при нулевых начальных условиях:

.

Для определения передаточной функции достаточно заменить исходную схему операторной схемой замещения, считая, что "внутренние" ЭДС индуктивности и емкости  и  равны нулю. После этого предполагаем, что на входе схемы замещения действует операторная ЭДС . Произведя расчет операторного изображения искомой переменной, делим его на .

Таким образом, операторная схема замещения будет иметь следующий вид:

Для расчета формулы  используем систему уравнений, применявшуюся при расчете цепи операторным методом, заменив в ней ненулевые начальные условия на нулевые:

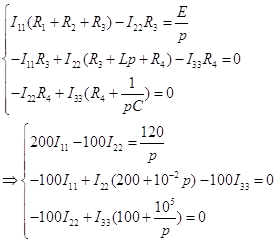
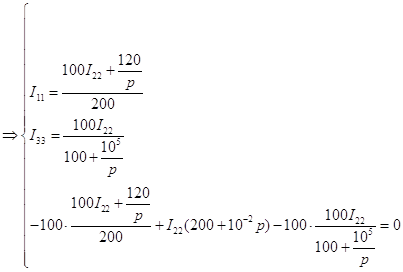
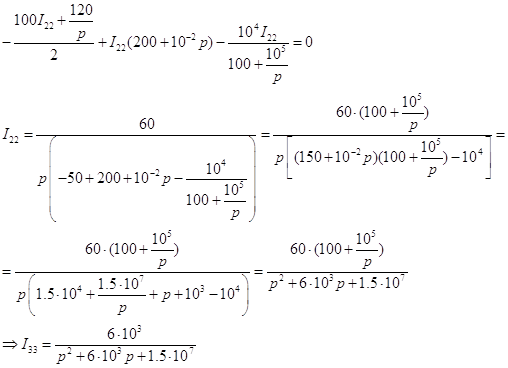
Так как , а , то

Таким образом передаточная функция между напряжениеv на емкости и входным напряжением на ЭДС равна

Составление переходной функции между заданными переменными

Переходной характеристикой цепи называется реакция участка цепи или всей цепи на воздействие согнала постоянной единичной величины.

Переходные характеристики удобно вычислять в операторной форме, используя выражение передаточной функции соответствующего вида.

Таким образом переходная функция по напряжению k(t) – закон изменения напряжения на зажимах некоторого участка цепи при подключении к источнику постоянной ЭДС в 1В при нулевых начальных условиях и отсутствии других источников.

Отображение по Лапласу переходной функции по напряжению  можно найти, используя формулу

Чтобы найти оригинал данного отображения воспользуемся теоремой разложения Хевисайда. Для этого определим корни знаменателя:

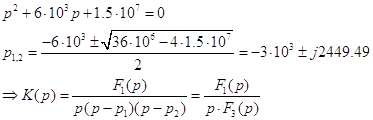
Так как в данном случае два корня комплексные сопряженные, а третий равен 0, то

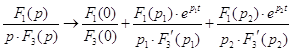, где

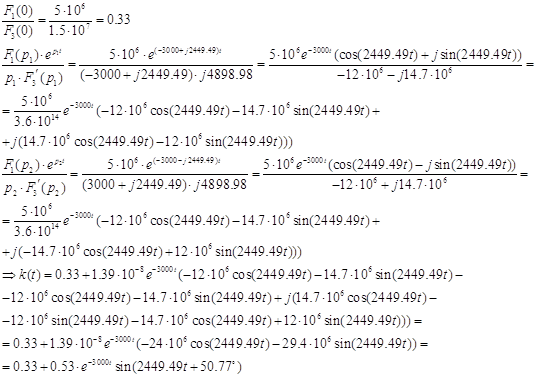
Таким образом переходная функция по напряжению равна

Расчет закона изменения искомой величины при подаче на вход цепи импульса заданной формы

Если на цепь воздействует сигнал произвольной формы, то необходимо разбить воздействие на отдельные участки, для которых может быть определен временной скачек, и рассматривать реакцию цепи в виде суммы участков на основании принципа наложения.

Для расчета реакции цепи на каждом участке используется интеграл Дюамеля:

Если воздействие имеет сложную форму, имеет скачи тока или напряжения, то интервал интегрирования разбивается на отдельные участки, и реакция цепи определяется для отдельных участков. При этом результаты не суммируются, а описываются для отдельных участков.

Для того, чтобы применить интеграл Дюамеля, необходимо определить закон изменения входного сигнала на каждом участке:

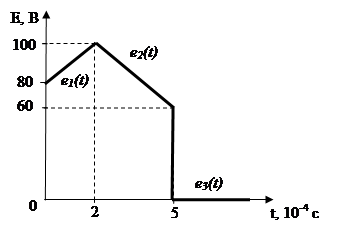
1.               

2.               

3.               

Таким образом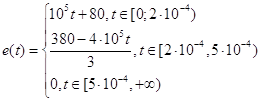

                  I.                       

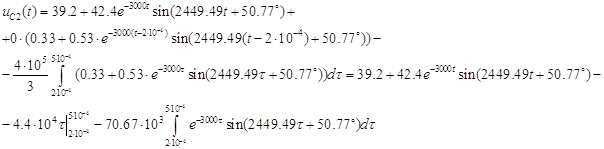
{интегрируем по частям, как в пункте I}=

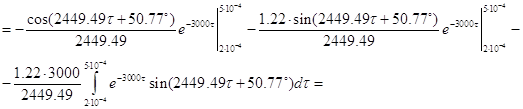
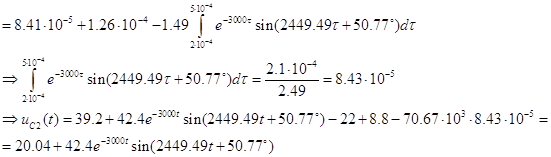
               II.                       

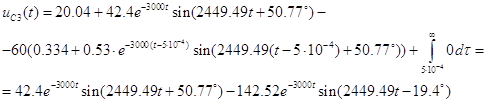
В результате получаем закон изменения искомой величины при подаче на вход цепи импульса заданной формы:

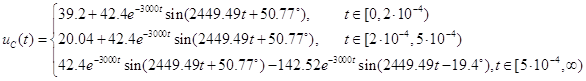
Расчет и построение графика спектральной плотности прямоугольного импульса

Основой спектрального анализа является то, что любой непрерывный сигнал можно представить как периодический с периодом . Энергия сигнала при этом не меняется. То есть каждая амплитуда гармонического ряда Фурье начинает убывать с ростом числа гармоник. Расстояние между отельными гармониками при увеличении их количества уменьшается. Но энергия спектра и его форма сохраняются.

Аналитическое описание в виде ряда Фурье преобразуется в аналитическое выражение в виде интеграла Фурье:

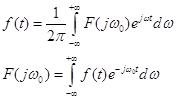
По условию дан одиночный импульс амплитудой E и длительностью tи=0,2мс:

Чтобы найти спектральную характеристику данного воздействия, представим с учетом принципа наложения его в виде двух сигналов, используя единичную функцию:

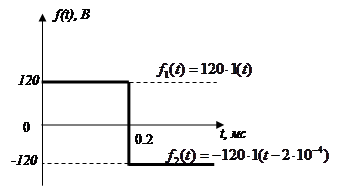
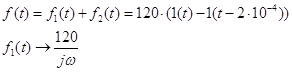
 (по теореме о запаздывание оригинала)

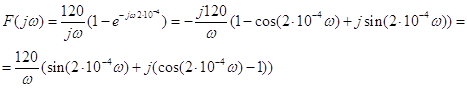
Полученная величина является спектральной плотностью сигнала f(t). Физическую ценность имеет модуль спектральной плотности сигнала , который согласно теореме Релея (правило Парсиваля) характеризует распределение энергии в спектре сигнала.

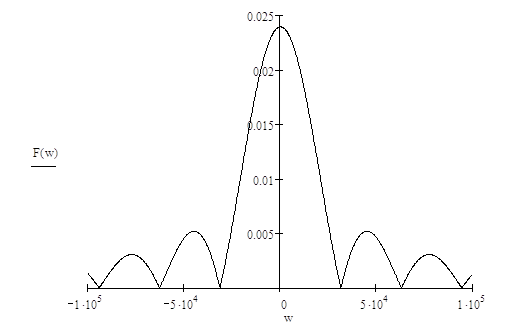
90℅ энергии сигнала сосредоточено в диапазоне частот первого лепестка графика, то есть в пределах от  до . В данном случае это соответствует изменению частоты от  до .

Расчет и построение графика спектральной плотности искомой переменной

Используя определение передаточной функции, можно записать, что . Заменив в этом равенстве оператор р на , получим формулу для нахождения спектральной плотности искомой величины:

Ранее было определено, что . Н(p) также была найдена.

Чтобы перейти к функции частоты, заменим оператор р на . В результате получим:

Таким образом получаем

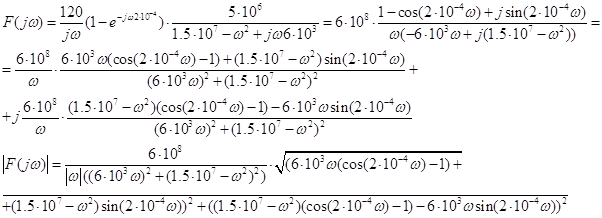
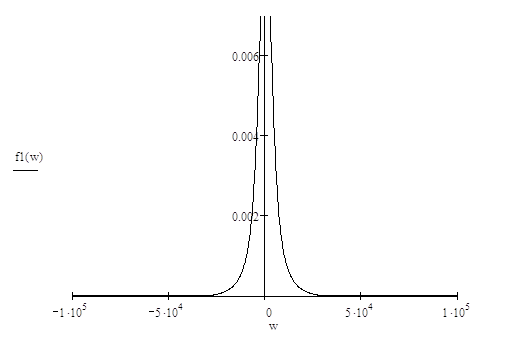
Список использованной литературы

1.                          Борисова Л.Ф. Конспект лекций по курсу "Основы теории цепей". – Мурманск: Изд-во МГТУ, 2007 г. – 157 с.

2.                          Шебес М.Р., Каблукова М.В. Задачник по теории линейных электрических цепей. Учеб. пособ. для эдектротехнич., радиотехнич. спец. вузов. – 4е изд., перераб. и доп. – М.: Высш. шк., 2000. – 379 с.

3.                          Методические указания к курсовой работе по курсу "Теоретические основы электротехники" для курсантов и студентов-заочников по специальности 1613 /Сост. Каценельсон Н.В., Докунин Е.А. – Мурманск, 2007. - 112