
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Статья: Аксиоматическое построение основных уравнений теории реального электромагнитного поля
Статья: Аксиоматическое построение основных уравнений теории реального электромагнитного поля
В.В. Сидоренков, МГТУ им. Н.Э. Баумана
В концепции корпускулярно-полевого дуализма электромагнитных характеристик материи сформулированы физико-математические принципы аксиоматического построения уравнений реального электромагнитного поля, физическое содержание которых представляет собой концептуально новый уровень в развитии основ полевой теории классического электромагнетизма.
Известно [1], что в электромагнетизме базовой физической характеристикой материального тела является его электрический заряд, представление о котором на микроуровне имеет принципиальное дополнение: элементарная частица характеризуется не только зарядом q, кратным заряду электрона |e-|, но и спином s, трактуемым как собственный момент количества движения частицы, величина которого квантована значением h/2, где h - постоянная Планка. Таким образом, локальными (корпускулярными) электромагнитными характеристиками микрочастицы являются электрический заряд, определяющий ее электрические свойства и собственный момент, ответственный за ее магнитные свойства, поскольку истинный магнетизм имеет спиновую природу.
С другой стороны, обратим внимание на основополагающую аксиому философии: «пространство и время есть формы существования материи», означающую невозможность в принципе существования материи вне пространства и времени, соответственно, реализации пространства и времени без материи. Иными словами, характеристики материи и пространства-времени едины и взаимно обусловлены. По нашему мнению, аксиома концептуально обосновывает реальность корпускулярно-полевого дуализма материи, который, казалось бы, отличен только лишь по названию от «корпускулярно-волнового дуализма» частиц микромира в квантовой механике. Формально и здесь и там имеем неразрывную взаимосвязь материи с ее пространственно-временным собственным полем. Однако сущностные различия принципиальны: представления корпускулярно-полевого дуализма основаны на объективном единстве частицы материи и ее поля в реальном пространстве физического вакуума, а в концепции корпускулярно-волнового дуализма материальная частица представляется волной вероятности в абсолютно пустом, абстрактном пространстве.
На
базе этой логики приходим к выводу, что и электромагнитные характеристики
микрообъектов должны обладать «корпускулярно-полевым дуализмом», благодаря
которому указанным выше локальным параметрам частицы соответствует некий
полевой аналог в виде ее собственного первичного поля. Такой вывод вовсе не так
тривиален, как может показаться на первый взгляд, ведь он относится не к
известному электромагнитному полю силового взаимодействия зарядов друг с другом
на расстоянии, а к иному, далеко не очевидному, первичному полю микрочастицы.
Более конкретно пока можно лишь сказать, что если такое поле действительно
реально, то оно обязательно должно быть функционально связано с обычным
векторным электромагнитным полем. По этой причине полагаем первичное поле также
векторным, где электрическая вектор-компонента ![]() порождена зарядом микрочастицы q,
а магнитная компонента
порождена зарядом микрочастицы q,
а магнитная компонента ![]() - удельным (на единицу заряда)
моментом n(
- удельным (на единицу заряда)
моментом n(![]() ),
кратным (n - натуральное число) кванту магнитного потока [1]. А поскольку
электрический заряд и спин выявляются опосредовано измерением характеристик
электромагнитного поля, то физически логично считать, что и компоненты
первичного поля предполагаемых корпускулярно-полевых пар будут также
определяться посредством того же электромагнитного поля.
),
кратным (n - натуральное число) кванту магнитного потока [1]. А поскольку
электрический заряд и спин выявляются опосредовано измерением характеристик
электромагнитного поля, то физически логично считать, что и компоненты
первичного поля предполагаемых корпускулярно-полевых пар будут также
определяться посредством того же электромагнитного поля.
Как
видим, наша основная задача - разобраться далее, что должно представлять собой
такое поле, каким образом можно аналитически описать его физические свойства и
в итоге аксиоматически построить уравнения функциональной взаимосвязи компонент
этого гипотетического поля ![]() и
и ![]() с реально наблюдаемыми в
настоящее время компонентами электромагнитного поля в виде электрической
с реально наблюдаемыми в
настоящее время компонентами электромагнитного поля в виде электрической ![]() и магнитной
и магнитной ![]() напряженностей.
напряженностей.
Можно попытаться уже сейчас поставить вопрос, каким должно быть обсуждаемое первичное поле. Например, известен физически интересный факт, что в волновое уравнение квантовой механики (уравнение Шрёдингера) входит поле векторного магнитного потенциала, которое в принципе не может быть заменено полем вектора магнитной индукции. Вполне возможно, что именно электрическая и магнитная компоненты поля векторного потенциала и есть первичные полевые характеристики микрочастицы, полевой эквивалент ее локальных параметров. Однако сегодня о физических свойствах электромагнитного векторного потенциала известно сравнительно мало, да и вообще пока не ясно, соответствует ли данное предположение действительности. Все это и многое другое мы должны выяснить в процессе проводимых исследований.
Итак,
продолжим наши рассуждения. Поскольку компоненты обсуждаемого гипотетического
первичного поля есть векторные функции пространственно-временных переменных, то
описывающие их поведение дифференциальные уравнения наиболее просто можно
получить действием на ![]() и
и ![]() пространственной производной
первого порядка (оператор «набла»)
пространственной производной
первого порядка (оператор «набла») ![]() со свойствами вектора и скалярной
частной временной производной
со свойствами вектора и скалярной
частной временной производной ![]() . При этом естественно возникает
принципиальный вопрос о допустимости именно таких математических действий с
точки зрения физического содержания получаемых результатов, их адекватности
рассматриваемой проблеме.
. При этом естественно возникает
принципиальный вопрос о допустимости именно таких математических действий с
точки зрения физического содержания получаемых результатов, их адекватности
рассматриваемой проблеме.
В
сложившейся ситуации воспользуемся чрезвычайно важным замечанием классика
электродинамики Дж.К. Максвелла, который настоятельно призывал [2] ответственно
относиться к математическим операциям над векторами электромагнитного поля и их
физической трактовке. Вот его слова ([2] п. 12): “В науке об электричестве
электродвижущая и магнитная напряженности принадлежат к величинам первого
класса – они определены относительно линии. ... Напротив, электрическая и
магнитная индукция, а также электрические токи принадлежат к величинам второго
класса – они определены относительно площади”. Как видим, тут конкретно
говорится о принципиальных различиях электромагнитных векторов: напряженностей ![]() и
и ![]() – линейных
(циркуляционных) векторов, соответственно, электрической
– линейных
(циркуляционных) векторов, соответственно, электрической ![]() и магнитной
и магнитной ![]() индукций,
плотности электрического тока
индукций,
плотности электрического тока ![]() – потоковых векторов. Здесь
материальные параметры среды:
– потоковых векторов. Здесь
материальные параметры среды: ![]() - электрическая и
- электрическая и ![]() - магнитная абсолютные
проницаемости,
- магнитная абсолютные
проницаемости, ![]() - удельная электропроводность.
- удельная электропроводность.
В
развитие сказанного далее Максвелл обсуждает корректные математические действия
над функциями полей указанных векторов с точки зрения физики ([2] п. 14): “В
случае напряженности следует брать интеграл вдоль линии от произведения
элемента длины этой линии на составляющую напряженности вдоль этого элемента.
В случае потоков следует брать интеграл по поверхности от потока через каждый
ее элементов”. Тогда в рамках таких условий при переходе к дифференциальной
форме записи этих математических действий операция «ротора» (см. теорему
Стокса) допустима только для полевых функций линейных векторов: ![]() и
и ![]() , а взятие «дивергенции»
(см. теорему Гаусса-Остроградского) возможно лишь от функций поля потоковых
векторов:
, а взятие «дивергенции»
(см. теорему Гаусса-Остроградского) возможно лишь от функций поля потоковых
векторов: ![]() ,
,
![]() и
и ![]() .
.
К
сожалению, призывы Максвелла к учету физико-математических различий функций
векторов электромагнитного поля обычно игнорируют, когда даже в учебной
литературе формально пишут физически бессмысленные выражения ![]() и
и ![]() , создавая путаницу
понятий в умах читателей, превращая в абсурд процесс познания, а обучение - в
бестолковое занятие. Как показывает практика научной работы и преподавание все
это следствие завидной живучести в умах самих «просветителей» (часто на
подсознательном уровне) инородной электродинамике гауссовой системы единиц с ее
безразмерными коэффициентами
, создавая путаницу
понятий в умах читателей, превращая в абсурд процесс познания, а обучение - в
бестолковое занятие. Как показывает практика научной работы и преподавание все
это следствие завидной живучести в умах самих «просветителей» (часто на
подсознательном уровне) инородной электродинамике гауссовой системы единиц с ее
безразмерными коэффициентами ![]() и
и ![]() , где векторы
, где векторы ![]() и
и ![]() ,
, ![]() и
и ![]() – тождественны. В итоге
выхолащивается физическое содержание в соотношениях электромагнетизма и
выпячивается на передний план формализм математики. Возможно, этот
математический нигилизм и есть одна из причин концептуального застоя в
классической электродинамике, которая после Максвелла как наука уже не
развивалась, несмотря на серьезную методическую модернизацию исходных
максвелловских уравнений и грандиозные успехи внедрения достижений
электромагнетизма во многих областях жизни человеческого общества.
– тождественны. В итоге
выхолащивается физическое содержание в соотношениях электромагнетизма и
выпячивается на передний план формализм математики. Возможно, этот
математический нигилизм и есть одна из причин концептуального застоя в
классической электродинамике, которая после Максвелла как наука уже не
развивалась, несмотря на серьезную методическую модернизацию исходных
максвелловских уравнений и грандиозные успехи внедрения достижений
электромагнетизма во многих областях жизни человеческого общества.
Странно, но сложившееся положение дел считается нормальным. Более того, повсеместно с помпой утверждается, что «данная область знания наиболее полно разработана во всех ее аспектах, и настоящий ее уровень является вершиной человеческого гения». Однако надо думать, что эти громкие заявления, конечно, не относятся собственно к самой электромагнитной теории, а касаются только математического уровня ее описания. Ведь математика - всего лишь язык физики. Правда, полезная глобальная математизация современных методов научных исследований порождает иллюзию, что именно уровень развития математики определяет сегодня прогресс наших знаний о Природе. Надо обладать немалым мужеством и веской аргументацией, чтобы в стремлении конструктивно изменить такую, казалось бы, тупиковую ситуацию во всеуслышание утверждать: физические представления классического электромагнетизма – это концептуально недостаточно исследованная область естествознания.
Итак,
рассмотрим действие оператора «набла» и частной временной производной на
векторные функции обсуждаемого здесь гипотетического первичного поля. Так как
для потоковых векторов, следуя здравой логике Максвелла, операция «ротора»
недопустима, то функции ![]() и
и ![]() считаем полями линейных векторов.
В этом случае мы получим два (из трех возможных) варианта записи действия
указанных операторов на представленные функции:
считаем полями линейных векторов.
В этом случае мы получим два (из трех возможных) варианта записи действия
указанных операторов на представленные функции: ![]() и
и ![]() ,
, ![]() и
и ![]() . А преобразование линейных
векторов
. А преобразование линейных
векторов ![]() и
и
![]() в потоковые
в потоковые
![]() и
и ![]() , аналогичные
известным потоковым векторам
, аналогичные
известным потоковым векторам ![]() и
и ![]() , описывающим отклик пространства
среды на воздействие этих полей, позволяет записать другой, скалярный результат
действия оператора «набла»:
, описывающим отклик пространства
среды на воздействие этих полей, позволяет записать другой, скалярный результат
действия оператора «набла»: ![]() и
и ![]() .
.
Эти
выражения используем далее для физико-математического построения соотношений
функциональной связи компонент гипотетического первичного поля ![]() и
и ![]() с компонентами
электромагнитного поля в виде электрической
с компонентами
электромагнитного поля в виде электрической ![]() и магнитной
и магнитной ![]() напряженностей.
Поскольку взятие ротора функции поля линейного вектора дает функцию потокового
вектора, то, дабы удовлетворить априорным требованиям взаимосвязи указанных
полей, физически логично считать, что циркуляция векторов
напряженностей.
Поскольку взятие ротора функции поля линейного вектора дает функцию потокового
вектора, то, дабы удовлетворить априорным требованиям взаимосвязи указанных
полей, физически логично считать, что циркуляция векторов ![]() и
и ![]() первичного поля
обусловлена явлением электрической
первичного поля
обусловлена явлением электрической ![]() и магнитной
и магнитной ![]() поляризации среды:
поляризации среды:
(a)
![]() , (b)
, (b) ![]() . (1)
. (1)
Здесь
учтено, что компонента ![]() первичного поля микрочастицы есть
полевой эквивалент ее электрического заряда, создающего электрическое поле, а
компонента
первичного поля микрочастицы есть
полевой эквивалент ее электрического заряда, создающего электрическое поле, а
компонента ![]() порождается
спином частицы, ответственным за магнитное поле.
порождается
спином частицы, ответственным за магнитное поле.
В
соотношениях (1) ротор функций не равен нулю, что говорит о том, что компоненты
первичного поля ![]() и
и ![]() являются вихревыми. По этой
причине дивергентные уравнения для указанных полевых компонент запишем в виде
соотношений кулоновской калибровки, определяющих математически чисто вихревой
характер таких полей:
являются вихревыми. По этой
причине дивергентные уравнения для указанных полевых компонент запишем в виде
соотношений кулоновской калибровки, определяющих математически чисто вихревой
характер таких полей:
(a)
![]() , (b)
, (b) ![]() . (2)
. (2)
Поскольку
действие скалярного оператора частной временной производной ![]() на векторную функцию не
меняет ее геометрические свойства, то получаемые при этом новые векторы
на векторную функцию не
меняет ее геометрические свойства, то получаемые при этом новые векторы ![]() и
и ![]() останутся
линейными (циркуляционными) векторами. А потому функциональная связь полей
останутся
линейными (циркуляционными) векторами. А потому функциональная связь полей ![]() или
или ![]() возможна
только с компонентами электромагнитного поля линейных векторов
возможна
только с компонентами электромагнитного поля линейных векторов ![]() и
и ![]() напряженностей, причем
для однозначного выбора пар этих компонент надо учесть, что равенство векторов
возможно только при их коллинеарности. В качестве существенного уточнения
заметим, что, согласно соотношениям (1), векторы в парах
напряженностей, причем
для однозначного выбора пар этих компонент надо учесть, что равенство векторов
возможно только при их коллинеарности. В качестве существенного уточнения
заметим, что, согласно соотношениям (1), векторы в парах ![]() и
и ![]() , соответственно,
, соответственно, ![]() и
и ![]() взаимно
ортогональны. Таким образом, с необходимостью приходим к соотношениям
взаимно
ортогональны. Таким образом, с необходимостью приходим к соотношениям ![]() и
и ![]() , которые,
однако, нельзя считать окончательными. Ведь в наших рассуждениях никак не
отражена принципиально важная характеристика материальной среды – ее
электрическая проводимость
, которые,
однако, нельзя считать окончательными. Ведь в наших рассуждениях никак не
отражена принципиально важная характеристика материальной среды – ее
электрическая проводимость ![]() , которой в той или иной мере
обладают все реальные среды. А это должно определенно повлиять на окончательный
вид данных выражений.
, которой в той или иной мере
обладают все реальные среды. А это должно определенно повлиять на окончательный
вид данных выражений.
Как
известно [1], процесс электропроводности в хорошем приближении описывается
законом Ома ![]() ,
где электрическое поле в проводнике с током потенциально:
,
где электрическое поле в проводнике с током потенциально: ![]() , то есть не может быть
вихревым. Следовательно, полученное ранее соотношение
, то есть не может быть
вихревым. Следовательно, полученное ранее соотношение ![]() является окончательным. Однако
вихревое магнитное поле электрического тока существует. Это следует из закона
сохранения заряда
является окончательным. Однако
вихревое магнитное поле электрического тока существует. Это следует из закона
сохранения заряда ![]() , когда подстановки в него
выражений закона Ома
, когда подстановки в него
выражений закона Ома ![]() , теоремы Гаусса
, теоремы Гаусса ![]() и соотношения (1а) дают
и соотношения (1а) дают
![]() , где
, где ![]() - объемная
плотность стороннего заряда, а
- объемная
плотность стороннего заряда, а ![]() - постоянная времени релаксации
заряда в среде за счет ее электропроводности. В итоге искомые соотношения для
вихревых
- постоянная времени релаксации
заряда в среде за счет ее электропроводности. В итоге искомые соотношения для
вихревых ![]() и
и
![]() полей
запишутся окончательно в виде
полей
запишутся окончательно в виде
(a)
![]() , (b)
, (b) ![]() . (3)
. (3)
Таким
образом, собирая полученные в наших физико-математических рассуждениях
соотношения (1) - (3) вместе, приходим к системе дифференциальных уравнений
функциональной взаимосвязи компонент нашего гипотетического поля ![]() и
и ![]() с реально наблюдаемыми
в настоящее время компонентами электромагнитного поля в виде электрической
с реально наблюдаемыми
в настоящее время компонентами электромагнитного поля в виде электрической ![]() и магнитной
и магнитной ![]() напряженностей:
напряженностей:
(a)
![]() , (b)
, (b) ![]() , (c)
, (c) ![]() ,
,
(d)
![]() , (e)
, (e) ![]() , (g)
, (g) ![]() . (4)
. (4)
Как
видим, данная система уравнений (4) описывает свойства необычного с точки
зрения традиционных представлений вихревого векторного электродинамического
поля, состоящего их четырех неразрывно связанных векторных компонент ![]() ,
, ![]() ,
, ![]() и
и ![]() , которое
условно можно назвать реальное электромагнитное поле.
, которое
условно можно назвать реальное электромагнитное поле.
Убедимся
теперь, что свойства функций компонент полей в нашей системе уравнений
действительно отвечают концепции корпускулярно-полевого дуализма
электромагнитных характеристик материи, благодаря которому конкретному
локальному параметру частицы соответствует свой полевой аналог в виде
собственного первичного поля. Вначале рассмотрим электрическую компоненту ![]() первичного
поля, причем для большей наглядности и математической общности представим
соотношение (4а) в интегральной форме:
первичного
поля, причем для большей наглядности и математической общности представим
соотношение (4а) в интегральной форме:
![]() . (5)
. (5)
Эти
интегральные соотношения устанавливают физически содержательное положение о
том, что величина циркуляции вектора ![]() по произвольному замкнутому контуру
С определяется электрическим потоком
по произвольному замкнутому контуру
С определяется электрическим потоком ![]() через поверхность
через поверхность ![]() , опирающуюся на этот
контур, то есть поляризационным электрическим зарядом, индуцированным на
указанной поверхности. Отсюда, в частности, следует определение поля вектора
электрического смещения
, опирающуюся на этот
контур, то есть поляризационным электрическим зарядом, индуцированным на
указанной поверхности. Отсюда, в частности, следует определение поля вектора
электрического смещения ![]() , по величине равного
поверхностной плотности поляризационного заряда
, по величине равного
поверхностной плотности поляризационного заряда ![]()
![]() на пробной площадке, ориентация
которой в данной точке создает на ней максимальное значение этого заряда, а
нормаль к площадке указывает направление вектора
на пробной площадке, ориентация
которой в данной точке создает на ней максимальное значение этого заряда, а
нормаль к площадке указывает направление вектора ![]() . Определение
. Определение ![]() как потокового вектора
показывает его принципиальное отличие от линейного (циркуляционного) вектора
напряженности
как потокового вектора
показывает его принципиальное отличие от линейного (циркуляционного) вектора
напряженности ![]() , являющегося силовой
характеристикой электрического поля.
, являющегося силовой
характеристикой электрического поля.
Таким
образом, согласно соотношению (5), электрическому заряду ![]() отвечает его полевой
эквивалент - электрическая векторная компонента
отвечает его полевой
эквивалент - электрическая векторная компонента ![]() первичного поля, размерность
которого есть линейная плотность электрического заряда. Итак, действительно
имеем реализацию первой фундаментальной корпускулярно-полевой пары
первичного поля, размерность
которого есть линейная плотность электрического заряда. Итак, действительно
имеем реализацию первой фундаментальной корпускулярно-полевой пары ![]() с единицами
измерения в системе СИ
с единицами
измерения в системе СИ ![]() .
.
Корпускулярно-полевые
представления подтверждаются связью напряженности магнитного поля ![]() и
электрической компоненты
и
электрической компоненты ![]() первичного поля посредством
соотношения (4с), имеющего в системе СИ единицу измерения
первичного поля посредством
соотношения (4с), имеющего в системе СИ единицу измерения ![]() , а ведь это, как и
должно быть, полевой эквивалент полного электрического тока
, а ведь это, как и
должно быть, полевой эквивалент полного электрического тока ![]() (токов проводимости и
смещения), величина (сила тока) которого имеет единицу измерения Ампер. Как
видим, соотношение (4с) для вихревых полей
(токов проводимости и
смещения), величина (сила тока) которого имеет единицу измерения Ампер. Как
видим, соотношение (4с) для вихревых полей ![]() и
и ![]() представляет собой полевую
составляющую корпускулярно-полевой пары
представляет собой полевую
составляющую корпускулярно-полевой пары ![]() , являющуюся очевидным прямым
физическим следствием первой фундаментальной пары.
, являющуюся очевидным прямым
физическим следствием первой фундаментальной пары.
Перейдем
теперь к магнитной компоненте ![]() первичного поля и проанализируем
соотношения связи поля вектора
первичного поля и проанализируем
соотношения связи поля вектора ![]() с полями векторов магнитной
индукции
с полями векторов магнитной
индукции ![]() (4d)
и электрической напряженности
(4d)
и электрической напряженности ![]() (4g). Рассмотрим вначале
соотношение (4d), которое представим в интегральной форме:
(4g). Рассмотрим вначале
соотношение (4d), которое представим в интегральной форме:
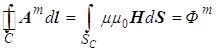 . (6)
. (6)
Видно,
что величина циркуляции вектора ![]() по контуру С определяется
магнитным потоком
по контуру С определяется
магнитным потоком ![]() через поверхность
через поверхность ![]() , опирающуюся на этот
контур, и имеет единицу измерения в СИ Вебер = (Джоуль∙секунда)/Кулон,
что соответствует модулю момента импульса на единицу заряда. При этом
размерность магнитной компоненты
, опирающуюся на этот
контур, и имеет единицу измерения в СИ Вебер = (Джоуль∙секунда)/Кулон,
что соответствует модулю момента импульса на единицу заряда. При этом
размерность магнитной компоненты ![]() первичного поля может быть
двоякой: либо импульс на единицу заряда, либо ей альтернативная линейная
плотность момента импульса на единицу заряда. Конечно, формально обе
размерности вектора
первичного поля может быть
двоякой: либо импульс на единицу заряда, либо ей альтернативная линейная
плотность момента импульса на единицу заряда. Конечно, формально обе
размерности вектора ![]() , выраженные через единицы
измерения, математически тождественны: (Ньютон
, выраженные через единицы
измерения, математически тождественны: (Ньютон![]() секунда)/Кулон = (Джоуль∙секунда)/(Кулон
секунда)/Кулон = (Джоуль∙секунда)/(Кулон![]() метр), но такое
равенство абсурдно физически, так как это принципиально различные величины.
метр), но такое
равенство абсурдно физически, так как это принципиально различные величины.
Для
нас здесь существенно то, что, согласно Максвеллу [2], в электромагнетизме
линейные (циркуляционные) векторы ![]() и
и ![]() имеют размерность линейной
плотности физической величины, а потоковые векторы
имеют размерность линейной
плотности физической величины, а потоковые векторы ![]() ,
, ![]() и
и ![]() – ее поверхностной плотности. В
частности, размерность вектора магнитной индукции
– ее поверхностной плотности. В
частности, размерность вектора магнитной индукции ![]() равна поверхностной плотности момента
импульса на единицу заряда в системе СИ Тесла = (Джоуль∙секунда)/(Кулон
равна поверхностной плотности момента
импульса на единицу заряда в системе СИ Тесла = (Джоуль∙секунда)/(Кулон![]() (метр
(метр![]() метр)).
Экспериментально это убедительно и ярко иллюстрируется эффектом Эйнштейна-де
Хааза [1], где в материальной среде при ее однородном намагничивании возникает
механический момент вращения, направленный коллинеарно полю, обусловленный
упорядочением под действием поля собственных магнитных моментов,
соответственно, моментов количества движения электронов в атомах вещества
среды. Следовательно, поле вектора
метр)).
Экспериментально это убедительно и ярко иллюстрируется эффектом Эйнштейна-де
Хааза [1], где в материальной среде при ее однородном намагничивании возникает
механический момент вращения, направленный коллинеарно полю, обусловленный
упорядочением под действием поля собственных магнитных моментов,
соответственно, моментов количества движения электронов в атомах вещества
среды. Следовательно, поле вектора ![]() определяет момент импульса
материальной среды, выявляющийся при ее намагничивании.
определяет момент импульса
материальной среды, выявляющийся при ее намагничивании.
Поэтому,
согласно соотношению (6), размерностью вихревого поля вектора ![]() следует считать
линейную плотность момента импульса на единицу заряда. Итак, локальной
характеристике микрочастицы - моменту импульса на единицу заряда -
сопоставляется его полевой эквивалент - магнитная компонента
следует считать
линейную плотность момента импульса на единицу заряда. Итак, локальной
характеристике микрочастицы - моменту импульса на единицу заряда -
сопоставляется его полевой эквивалент - магнитная компонента ![]() первичного поля, что
дает вторую фундаментальную корпускулярно-полевую пару, которую, например,
конкретно для электрона можно записать как
первичного поля, что
дает вторую фундаментальную корпускулярно-полевую пару, которую, например,
конкретно для электрона можно записать как ![]() с единицами измерения в системе
СИ
с единицами измерения в системе
СИ ![]() .
.
Далее
обратимся к соотношению (4g) связи векторов ![]() и
и ![]() , где вектор
, где вектор ![]() определен производной
по времени от момента импульса
определен производной
по времени от момента импульса ![]() . Тогда размерность вихревого поля
электрической напряженности
. Тогда размерность вихревого поля
электрической напряженности ![]() однозначно равна линейной
плотности момента силы на единицу заряда, что никоим образом не опровергает
традиционные единицы измерения этого вектора Вольт/метр либо Ньютон/Кулон, а
лишь уточняет его физический смысл. Таким образом, соотношение (4g)
представляет собой полевой аналог основного уравнения динамики вращательного
движения твердого тела в механике, что согласуется с представлениями
корпускулярно-полевого дуализма характеристик материи.
однозначно равна линейной
плотности момента силы на единицу заряда, что никоим образом не опровергает
традиционные единицы измерения этого вектора Вольт/метр либо Ньютон/Кулон, а
лишь уточняет его физический смысл. Таким образом, соотношение (4g)
представляет собой полевой аналог основного уравнения динамики вращательного
движения твердого тела в механике, что согласуется с представлениями
корпускулярно-полевого дуализма характеристик материи.
Логика
требует, что если электродинамические уравнения (4), согласно реализованному
здесь плану их построения, являются основополагающими в электромагнитной
теории, то обязательным тривиальным следствием из них должна быть система
традиционных уравнений Максвелла классической электродинамики для полей ![]() и
и ![]() напряженностей.
И действительно, векторное действие оператора «набла» на соотношения (4c) и
(4g) с подстановкой в этот результат соотношений (4a) и (4d), и,
соответственно, скалярное действие оператора «набла» на (4a) и (4d) дают нам
классические уравнения электромагнитного поля для случая сред с локальной
электронейтральностью (
напряженностей.
И действительно, векторное действие оператора «набла» на соотношения (4c) и
(4g) с подстановкой в этот результат соотношений (4a) и (4d), и,
соответственно, скалярное действие оператора «набла» на (4a) и (4d) дают нам
классические уравнения электромагнитного поля для случая сред с локальной
электронейтральностью (![]() ):
):
(a)
![]() , (b)
, (b) ![]() ,
,
(c)
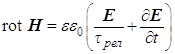 , (d)
, (d) ![]() . (7)
. (7)
Принципиальная особенность этих уравнений состоит в том, что в их структуре заложена отражающая обобщение опытных данных основная аксиома классической электродинамики – неразрывное единство переменных во времени электрической и магнитной компонент электромагнитного поля, распространяющихся в свободном пространстве в виде поперечных волн. Например, из (7) получим волновое уравнение для электрической напряженности:
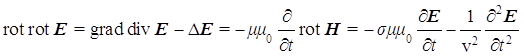 ,
,
где
![]() -
фазовая скорость волны в отсутствие поглощения (
-
фазовая скорость волны в отсутствие поглощения (![]() ).
).
Уравнения (7) отвечают также на вопрос о переносе этими волнами электромагнитной энергии, закон сохранения которой аналитически сформулирован в так называемой теореме Пойнтинга:
![]() . (8)
. (8)
Здесь
поступающий извне поток энергии ![]() компенсирует в данной точке среды
джоулевы (тепловые) потери при электропроводности (первое слагаемое справа) и
изменяет электрическую и магнитную энергии, либо наоборот.
компенсирует в данной точке среды
джоулевы (тепловые) потери при электропроводности (первое слагаемое справа) и
изменяет электрическую и магнитную энергии, либо наоборот.
Сделаем
важное замечание. Полученные из более общей системы уравнений (4) уравнения
Максвелла (7) отвечают на центральный вопрос наших исследований: что
представляет собой введенное на основе корпускулярно-полевого дуализма
электромагнитных характеристик материи собственное первичное поле микрочастицы.
Ответ формулируется так: если дивергенция ротора любого векторного поля
тождественно равна нулю, то из дивергентного уравнения (7b) ![]() следует соотношение (4a),
соответственно, из (7d)
следует соотношение (4a),
соответственно, из (7d) ![]() имеем соотношение (4d),
посредством которых вводят понятие именно компонент векторного
электромагнитного потенциала. Кстати, компоненты указанного потенциала физически
следует считать поляризационными потенциалами. Таким образом, мы убедились, что
компоненты гипотетического первичного поля
имеем соотношение (4d),
посредством которых вводят понятие именно компонент векторного
электромагнитного потенциала. Кстати, компоненты указанного потенциала физически
следует считать поляризационными потенциалами. Таким образом, мы убедились, что
компоненты гипотетического первичного поля ![]() и
и ![]() действительно однозначно являются
полями соответственно электрической и магнитной компонент векторного
потенциала, которые, как показано выше, а также, например, в [4], по их
физическому смыслу есть полевые эквиваленты соответствующих локальных
электромагнитных параметров частиц материи.
действительно однозначно являются
полями соответственно электрической и магнитной компонент векторного
потенциала, которые, как показано выше, а также, например, в [4], по их
физическому смыслу есть полевые эквиваленты соответствующих локальных
электромагнитных параметров частиц материи.
И
еще важное. Из уравнений (4) также следуют структурно аналогичные системе (7)
еще три системы уравнений для других пар вихревых компонент реального
электромагнитного поля. Их можно получить действием оператора «набла» на
соответствующие выражения в системе уравнений (4), аналогично выводу системы
уравнений Максвелла (7). Уравнения в этих системах (см. работы [3, 4])
рассматривают такие области пространства, где присутствует либо только поле
электромагнитного векторного потенциала с электрической ![]() и магнитной
и магнитной ![]() компонентами:
компонентами:
(a)
![]() , (b)
, (b) ![]() ,
,
(c)
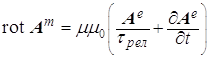 , (d)
, (d) ![]() ; (9)
; (9)
либо
электрическое поле с компонентами ![]() и
и ![]()
(a)
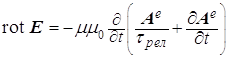 , (b)
, (b) ![]() ,
,
(c)
![]() , (d)
, (d) ![]() ; (10)
; (10)
либо,
наконец, магнитное поле с компонентами ![]() и
и ![]() .
.
(a)
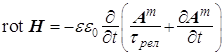 , (b)
, (b) ![]() ,
,
(c)
![]() , (d)
, (d) ![]() . (11)
. (11)
Как и следовало ожидать, из этих новых систем электродинамических уравнений аналогично выводу формулы (8) непосредственно получаем соотношения баланса:
для потока момента ЭМ импульса из уравнений системы (9)
![]() (12)
(12)
для потока электрической энергии из уравнений системы (10)
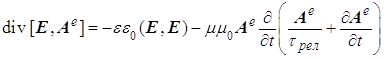 (13)
(13)
и, наконец, для потока магнитной энергии из уравнений системы (11)
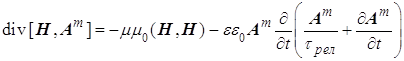 . (14)
. (14)
Поскольку дивергенция по определению есть объемная плотность потока векторного поля в данной точке, то соотношения баланса (8) и (12) - (14) показывают, что наличие (соответственно, изменение) определенной величины энергии или момента импульса в рассматриваемой точке невозможно в отрыве от окружающего пространства, без взаимодействия с ним посредством потоковой связи извне. Существенно, что это не является чем-то специфическим или необычным. Вот, например, тривиально наглядная ситуация: растянутая руками пружина, где ее внутренняя энергия упругой деформации создается и существует только за счет взаимодействия с окружением (действия рук). Итак, именно соотношения баланса, являющиеся следствием систем уравнений (7) и (9) - (11), однозначно иллюстрируют реальность корпускулярно-полевого дуализма характеристик материи, использование концепции которого позволило построить систему электродинамических уравнений (4) первичной функциональной взаимосвязи теперь уже конкретно компонент поля электромагнитного векторного потенциала и электромагнитного поля, тем самым поднять на новый концептуальный уровень физические представления полевой теории классического электромагнетизма.
Таким
образом, аргументированно показано, что в Природе объективно существует весьма
сложное и необычное с точки зрения традиционных представлений четырехвекторное
вихревое поле в виде совокупности функционально неразрывно связанных между
собой вихрево-полевых компонент ![]() ,
, ![]() и
и ![]() ,
, ![]() . Относительно наблюдения его
физических проявлений такое поле реализуется четверкой составляющих его
электродинамических полей из пар вышеуказанных компонент. Здесь поле
электромагнитного векторного потенциала с компонентами
. Относительно наблюдения его
физических проявлений такое поле реализуется четверкой составляющих его
электродинамических полей из пар вышеуказанных компонент. Здесь поле
электромагнитного векторного потенциала с компонентами ![]() и
и ![]() описывается системой уравнений
(9), электромагнитное поле с
описывается системой уравнений
(9), электромагнитное поле с ![]() и
и ![]() - системой (7), электрическое
поле с
- системой (7), электрическое
поле с ![]() и
и ![]() - системой
(10), наконец, магнитное поле с
- системой
(10), наконец, магнитное поле с ![]() и
и ![]() - системой (11). Причем такие
структурные образования из двух векторных взаимно ортогональных полевых
компонент делают принципиально возможным перемещение в пространстве конкретного
электродинамического поля в виде потока соответствующей физической величины
(см. соотношения (8), (12) - (14)). Подробно характеристики и специфика
распространения волн таких полей рассмотрены, например, в работе [5].
- системой (11). Причем такие
структурные образования из двух векторных взаимно ортогональных полевых
компонент делают принципиально возможным перемещение в пространстве конкретного
электродинамического поля в виде потока соответствующей физической величины
(см. соотношения (8), (12) - (14)). Подробно характеристики и специфика
распространения волн таких полей рассмотрены, например, в работе [5].
Как видим, описывающие все эти поля электродинамические соотношения (4) объективно являются первичными основополагающими уравнениями современной полевой теории электромагнетизма, которые с их следствиями: системами уравнений (7) и (9) - (11) представляют фундамент классической электродинамики. Заметим в этой связи, что методически серьезных проблем не должно возникнуть, если обсуждаемое здесь реальное электромагнитное поле сохранит за собой традиционное в электромагнетизме нынешнее название – электромагнитное поле с учетом развития физических воззрений и его нового содержания.
Список литературы
1. Тамм И.Е. Основы теории электричества. - М.: Наука, 1989.
2. Максвелл Дж.К. Трактат об электричестве и магнетизме. Том I и II. - М.: Наука, 1989.
3. Сидоренков В.В. Обобщение физических представлений о векторных потенциалах в классической электродинамике // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2006. № 1. С. 28-37.
4. Сидоренков В.В. Фундаментальные основы электродинамической теории нетеплового действия электромагнитных полей на материальные среды // Вестник Воронежского государственного технического университета. 2007. Т. 3. № 11. С. 75-82.
5. Сидоренков В.В. Анализ и решение проблемы переноса энергии волнами электромагнитного поля // http://www.referat.ru/pub/item/28887 .
Для подготовки данной работы были использованы материалы с сайта http://referat.ru/
© 2009 База Рефератов