Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Учебное пособие: Кинематика
Учебное пособие: Кинематика
Кинематика
тема 1 кинематика точки
1.1 предмет изучения
С самого рождения и на протяжении всей своей жизни мы встречаемся с движением материи. Простейшей формой движения материи является механика. В разделе «кинематика» мы будем изучать только одну сторону механического движения – геометрическую, т.е. мы будем изучать геометрию движения тела без учета его массы и сил, действующих на него. Механически движение в общем смысле будет изучаться в разделе «динамика».
Под движением в механике мы будем понимать перемещение данного тела в пространстве и времени по отношению к другим телам.
Для определения положения движущего тела вводится система отсчета, связанная с телом, условно принимаемым за неподвижное. Движение тела происходит в пространстве и времени. Мы будем рассматривать трехмерное эвклидо пространство. За единицу длины в нем принимается 1 метр. Время считается универсальным, т. е. не зависящим от выбранной системы отсчета. За единицу времени принимается 1 секунда. В задачах механики время принимается за независимую переменную. Все остальные кинематические величины (расстояния, скорости, ускорения и т.д.) являются функциями времени.
Прежде чем изучать движение его необходимо задать, т.е. описать каким-либо математическими формулами так, чтобы можно было узнать положение тела и все его кинематические характеристики в любой момент времени.
Основная задача
кинематики заключается в том, чтобы по известному закону движения тела (или
какой-либо его точки) найти все остальные
кинематические характеристики движения.
Изучение кинематики мы начнем с изучения движения простейшего тела – точки, т.е. такого тела, размерами которого можно пренебречь и рассматривать его как геометрическую точку.
1.2 Способы задания движения точки
Мы будем рассматривать три способа задания движения: векторный, координатный и естественный.
1.2.1 Векторный способ
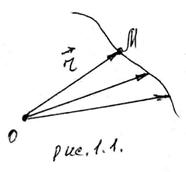
Положение движущейся
точки М определяется с помощью радиуса вектора ![]() ,
проведенного из некоторого неподвижного центра О в эту точку (рис. 1.1).
В процессе движения этот вектор изменяется по величине и направлению, т.е.
является функцией времени. Зависимость
,
проведенного из некоторого неподвижного центра О в эту точку (рис. 1.1).
В процессе движения этот вектор изменяется по величине и направлению, т.е.
является функцией времени. Зависимость
![]() (1.1)
(1.1)
называется уравнением движения (или законом движения) в векторной форме. Линия, описываемая концом этого вектора называется траекторией движения.
|
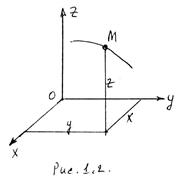
1.2.2 Координатный способ
С неподвижным центром О связывается неподвижная система координат ОХ у Z. Положение точки определяется тремя координатами: х, у, z (рис. 1.2). В процессе движения эти координаты изменяются, т.е. они являются функциями времени.
|
Зависимости
х=f1(t); у=f2(t); z=f3(t) (1.2)
называются уравнениями движения точки в координатной форме. Эти уравнения являются одновременно параметрическими уравнениями траектории движения (параметром является t).
Чтобы получить уравнение траектории в явной форме, надо из уравнений (1.2) исключить параметр t.
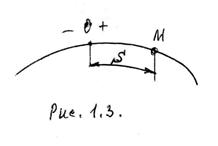
1.2.3 Естественный способ
При естественном способе задания движения траектория заранее известна. На траектории выбирается начало отсчета (т. 0) и устанавливается положи-тельное и отрицательное направления отсчета.
Положение точки на траектории однозначно определяется криволинейной координатой S, измеряемой вдоль траектории. Зависимость
S = f(t) (1.3)
называется уравнением движения в естественной форме.
|
1.2.4 Связь между способами задания движения
Координатный векторный способы связаны зависимостью:
![]() (1.4)
(1.4)
где ![]() - единичные орты координатных осей.
- единичные орты координатных осей.
Переход от координатного способа к естественному:
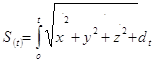
здесь: ![]() ;
; 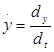
![]()
(т.е. здесь и в дальнейшем производная по времени обозначается точкой над буквой).
1.3 Определение скорости и ускорение точки при векторном задании движения
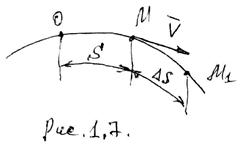
Пусть точка за время ![]() переходит из положения М в положение М1,
двигаясь вдоль траектории (Рис. 1.4)
переходит из положения М в положение М1,
двигаясь вдоль траектории (Рис. 1.4) ![]() называется вектором
перемеще-ния.
называется вектором
перемеще-ния. 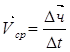 - средняя скорость.
- средняя скорость.
Например, вектор ![]() по хорде М М1. если уменьшать промежуток времени
по хорде М М1. если уменьшать промежуток времени ![]() , то хорда будет приближаться к касательной,
а средняя скорость к мгновенной.
, то хорда будет приближаться к касательной,
а средняя скорость к мгновенной.
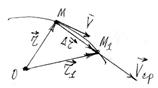
Рис. 1.4
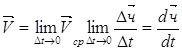
![]() (1.6)
(1.6)
Направлен вектор скорости по касательной к траектории.
Определение ускорения:
Пусть в положении М
скорость ![]() , а в положении М1 (через
время
, а в положении М1 (через
время ![]() ) скорость
) скорость ![]() .
Приращение скорости
.
Приращение скорости ![]() (рис. 1.5).
(рис. 1.5).
Среднее ускорение:
![]()
Ускорение в данный момент
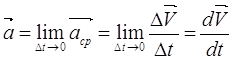
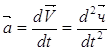 (1.7)
(1.7)
Лежит вектор ускорения в плоскости, проведенных через касательной к траектории в двух бесконечно близких точках. Эта плоскость называется соприкасающейся или плоскостью главной кривизны.
1.4 Определение скорости и ускорения точки при координатном способе задания движения
при координатном способе задания движения:
![]() (а)
(а)
с другой стороны:
![]() (б)
(б)
Сравнивая (а) и (б) находим:
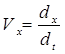 ;
; 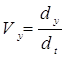 ;
; 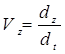 (1.8)
(1.8)
т.е. проекция вектора скорости на оси координат равны первым производным по времени от соответствующих координат.
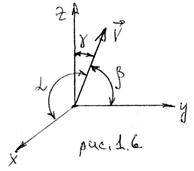
Величина скорости:
![]() (1.9)
(1.9)
направление вектора скорости определяется с помощью направляющих косинусов, т.е. косинусов углов между вектором скорости и осями координат (рис. 1.6).
|
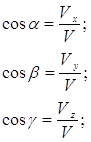 (1.10)
(1.10)
Аналогично ищем ускорения:
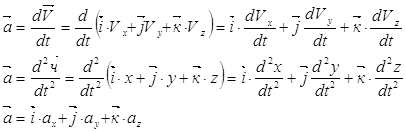
Сравнивая (в), (г), (д) находим:
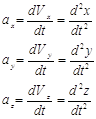 (1.11)
(1.11)
Проекция ускорения равны первым производным по времени от соответствующих проекций скорости или вторым производным по времени от соответствующих координат.
Величина ускорения:
![]() (1.12)
(1.12)
Направляющие косинусы:
![]() ;
; ![]() ;
; ![]() ; (1.13)
; (1.13)
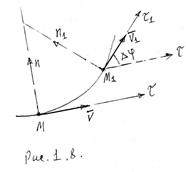
1.5 Определение скорости и ускорения точки при естественном задании движения
Пусть за время ![]() точка переместилась из положения М в
положение М1, совершив перемещение
точка переместилась из положения М в
положение М1, совершив перемещение ![]() (рис.
1.17).
(рис.
1.17).
|
величина скорости точки:
![]()
![]()
![]() (1.14)
(1.14)
Направлена скорость по касательной к траектории:
Найдем ускорение точки.
Пусть в положении М
точка имеет скорость ![]() (рис. 1.8).
(рис. 1.8).
Полное ускорение точки будет:
![]()
![]()
![]()
Обозначим угол между
касательными через ![]() (угол смежности). Спроецируем
вектор ускорения
(угол смежности). Спроецируем
вектор ускорения ![]() на касательную
на касательную ![]() и нормам п.
и нормам п.
![]()
![]()
|
Найдем эти пределы,
учитывая, что при ![]() одновременно и
одновременно и ![]() и
и ![]() .
.
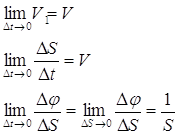
где ρ радиус кривизны траектории в данной точке.
Подставив эти значения в ап получим:
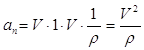
Т.о. величины касательного, нормального и полного ускорений определяется формулами:
|
|
|
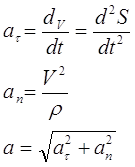
Касательное ускорение направлено по касательной к траектории (в сторону скорости при ускоренном движении и противоположно скорости – при замедленном) и характеризует изменение величины скорости.
Нормальное ускорение направлено по нормам к траектории к центру кривизны и характеризует изменение направления скорости.
1.6 Частные случаи движения точки
По виду траектории движение делится на прямолинейное и криволинейное. При прямолинейном движении ап = 0, т.к. ρ = ∞.
По изменению величины скорости движения делится на равномерные и неравномерные.
Движение называется равномерным, если величина скорости постоянна (V=const).
Закон равномерного движения:
S=S0+Vt (1.18)
Движение называется равномерным, если величина касательного ускорения постоянна.
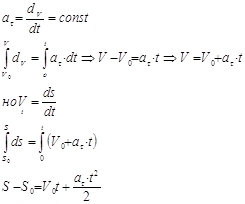
Т.о. равномерное движение описывается двумя формулами:
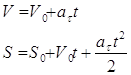 (1.19)
(1.19)
Нормальное ускорение направлено от данной точки к оси вращения
Тема 2 Простейшие движения тела
К простейшим движениям твердого тела относятся поступательное движение и вращательное движение вокруг неподвижной оси.
2.1 Поступательное движение твердого тела
Поступательным называется такое движение тела, при котором любой отрезок прямой проведенной в теле перемещается параллельно самому себе.
Это самое простое движение тела.
Оно описывается одной теоремой:
При поступательном движении тела все его точки описывают одинаковые, при наложении совпадающие траектории, и имеют одинаковые скорости и одинаковые ускорения.
Доказательство:
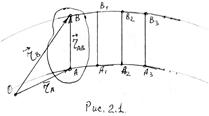
Проведем в теле произвольный отрезок АВ. При движении тела он остается параллельным самому себе (рис. 2.1). траектория точки А на величину АВ, т.е. они одинаковые.
|
Проведем из неподвижного
центра О радиусы-векторы точек А и В (![]() ), а также вектор
), а также вектор ![]() из точки А
в точку В.
из точки А
в точку В.
Очевидно, что
![]()
Продифференцируем это
векторное равенство по времени, учитывая, что ![]() .
.
![]() ; но
; но
![]() , значит
, значит
![]() (2.1)
(2.1)
дифференцируя (2.1) по времени: ![]() , получаем:
, получаем:
![]() (2.2)
(2.2)
Так как точки А и В взяты произвольно, то все выводы справедливы для всех точек тела.
Следовательно, при поступательном движении тела его можно считать точкой и пользоваться формулами кинематики точки.
2.2 Вращение тела вокруг неподвижной оси
Вращательным называется такое движение тела, при котором хотя бы две точки, принадлежащие телу или жестко с ним связанные, во все время движения остаются неподвижными. Прямая, проходящая через эти две неподвижные точки называется осью вращения.
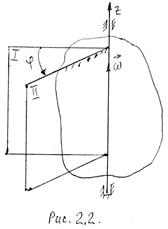
Проведем через ось вращения две полуплоскости: неподвижную І и подвижную II, жестко связанную с телом и вращающуюся вместе с ним (рис. 2.2).
Положением тела будет однозначно определяться углом φ между этими полуплоскостями. Угол φ называется углом поворота. Измеряется он в радианах. Положительное направление φ против часовой стрелки, если смотреть навстречу оси Z.
Зависимость
φ = φ(t) (2.3)
называется уравнением вращательного движения.
|
Быстрота вращения характеризуется угловой скоростью ω. Средняя угловая скорость определяется как отношения приращения угла поворота ∆φ к промежутку времени ∆t, за который оно произошло.
![]()
Угловая скорость в данный момент времени:
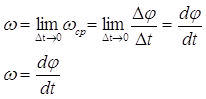 (2.3)
(2.3)
Вектор угловой скорости ![]() направлен по оси вращения в ту сторону,
чтобы, глядя навстречу ему, мы видели вращение происходящей против часовой
стрелки. Изменяется ω в радиан/сек. На производстве угловую
скорость измеряют в об/мин. В этом случае она обозначается буквой «п».
направлен по оси вращения в ту сторону,
чтобы, глядя навстречу ему, мы видели вращение происходящей против часовой
стрелки. Изменяется ω в радиан/сек. На производстве угловую
скорость измеряют в об/мин. В этом случае она обозначается буквой «п».
Формула перехода:
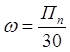 (2.4)
(2.4)
Изменение угловой скорости характеризуется угловым ускорением ε, которая определяется как первая производная от угловой скорости или вторая производная от угла поворота по времени:
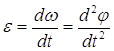 (2.5)
(2.5)
Направлен вектор ![]() также по оси вращения в сторону
также по оси вращения в сторону ![]() при ускоренном и противоположном
при ускоренном и противоположном ![]() при замедленном вращении. Единица измерения
1Рад/с2.
при замедленном вращении. Единица измерения
1Рад/с2.
2.3 Равномерное и равнопеременное вращение
Вращение называется равномерным, если угловая скорость постоянна, т.е. ω = const.
Закон равномерного вращения:
φ=φ0+ωt (2.6)
Вращение называется равнопеременным, если угловое ускорение постоянно, т.е. ε = const.
Но ![]() . Разделяя переменные и интеграции
. Разделяя переменные и интеграции 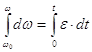 находим, что
находим, что
![]() (2.7)
(2.7)
Подставив сюда ![]() и еще раз интегрируя
и еще раз интегрируя 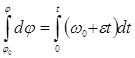 ,
получим уравнение переменного вращения:
,
получим уравнение переменного вращения:
![]() (2.8)
(2.8)
2.4 Скорости и ускорение точек вращающегося тела
пусть за время dt тело повернулось на угол dφ, а точка М, находящаяся на расстоянии R от оси вращения, получила перемещение dS=ч* dφ (рис. 2.3).
Тогда скорость точки
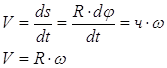 (2.9)
(2.9)
Направлен вектор скорости
![]() по касательной к траекториям, т.е. по
касательной к окружности радиуса R, центр которой лежит на оси вращения, а ее плоскость перпендикулярна оси
вращения.
по касательной к траекториям, т.е. по
касательной к окружности радиуса R, центр которой лежит на оси вращения, а ее плоскость перпендикулярна оси
вращения.
Найдем нормальное и касательное ускорение точки:
|
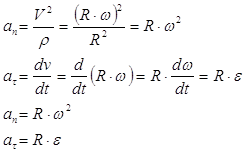
|
||||
Нормальное ускорение направлено от данной точки к оси вращения.
Касательное ускорение направлено по касательной к округлости, которую описывает точка и совпадает с направлением скорости при ускоренном вращении, а при немедленном противоположно скорости.
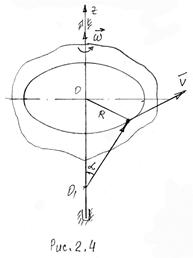
Рассмотрим векторное
произведение ![]() (рис. 2.4). Его модуль
(рис. 2.4). Его модуль ![]() , а направление совпадает с направлением
скорости. Из этого делаем вывод, что вектор скорости:
, а направление совпадает с направлением
скорости. Из этого делаем вывод, что вектор скорости:
![]() (2.11)
(2.11)
взяв от этого выражения производную по времени, получим:
![]()
Первое произведение по величине и направлению совпадает с касательным, а вторая – с нормальным ускорением.
Таким образом, касательная и нормальная составляющие вектора полного ускорения при вращательном движении определяется формулами:
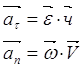 (2.12)
(2.12)
|
Отметим, что
радиус-вектор ![]() точки М можно проводить из
любой точки О1, лежащей на оси вращения (все точки оси
вращения неподвижны) и что этот вектор постоянный по модулю (у него меняется только
направление).
точки М можно проводить из
любой точки О1, лежащей на оси вращения (все точки оси
вращения неподвижны) и что этот вектор постоянный по модулю (у него меняется только
направление).
2.5 Простейшие передаточные механизмы
Передаточными называют механизмы, служащие для передачи вращения с одного вала на другой. К простейшим из них относятся: зубчатые, ременные, цепные и фрикционные. Схематическое изображение зубчатых и фрикционных механизмов показано на рис. 2.5а, а ременных и цепных на рис. 2.5.б.
Найдем скорость точки а: ![]() на колесе
І и
на колесе
І и ![]() на колесе
ІІ. Так как проскальзывание
отсутствует, то
на колесе
ІІ. Так как проскальзывание
отсутствует, то ![]() .
.
Отсюда:
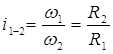 (2.13)
(2.13)
т.е. угловые скорости обратно пропорциональны радиусом колес. Величина i1-2 называется передаточным отношением.
У зубчатых и цепных передач – передаточное отношение точное, у ременных и фрикционных – может быть проскальзывание. Ременные и цепные передачи позволяют передавать вращение на большие расстояния, чем зубчатые и фрикционные. С устройством передаточных механизмов, их изготовлением, расчетами и эксплуатацией вы познакомитесь в курсах «Теория механизмов и машин» и «Детали машин».
Тема 3 Сложное движение точки
3.1 Основные определения
До сих пор мы рассматриваем движение точки в одной, неподвижной системе отсчета. Однако, часто встречаются случаи, когда точка движется по определенному закону в некоторой системе отсчета, которая, в свою очередь, перемещается относительно неподвижной системы отсчета. Такое движение точки называется сложным. Введем основные определения сложного движения точки.
Движение точки в
подвижной системе отсчета называется относительным. Скорость и ускорение точки
в этом движении называются относительными и обозначаются: ![]() (или
(или ![]() ).
).
Движение точки вместе с
подвижной системой называется переносным. Скорость и ускорение той точки М/
подвижной системы, в которой в данный момент находится движущаяся точка М,
являются для данной точки переносной скоростью и переносным ускорением и
обозначаются ![]() (или
(или ![]() ).
).
Движение точки
относительно неподвижной системы отсчета называется абсолютным. Скорость и
ускорение точки в этом движении называются абсолютными и обозначаются ![]() (или
(или ![]() ).
).
Пусть точка М движется в подвижной системе отсчета охуz. Ее координаты х, у, z являются функциями времени, а координаты х/, у/, z/ точки М/ подвижной системы, в которой в данный момент находится движущая точка М, являются константами. Но в любой момент времени
х = х/, у = у/, z = z/ (3.1)
Введем в рассмотрение радиусы-векторы, определяющие положение точек М и М/ в подвижной и неподвижной системах отсчета (рис. 3.1).
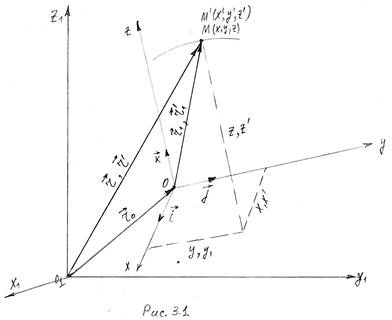
![]() -
радиус-вектор, определяющий положение начала подвижной системы охуz в неподвижной системе отсчета о1х1у1z1.
-
радиус-вектор, определяющий положение начала подвижной системы охуz в неподвижной системе отсчета о1х1у1z1.
![]() =
=![]() - радиус-вектор, определяющий положение
движущейся точки М в подвижной системе отсчета. Он описывает относительное
движение точки.
- радиус-вектор, определяющий положение
движущейся точки М в подвижной системе отсчета. Он описывает относительное
движение точки.
![]() -
радиус-вектор, определяющий положение точки М/ подвижной системы в
этой же системе.
-
радиус-вектор, определяющий положение точки М/ подвижной системы в
этой же системе.
![]() -
радиус-вектор, определяющий положение точки М/ подвижной
системы в неподвижной системе отсчета. Он описывает переносное движение точки.
-
радиус-вектор, определяющий положение точки М/ подвижной
системы в неподвижной системе отсчета. Он описывает переносное движение точки.
![]() -
радиус-вектор, определяющий положение движущейся точки М в неподвижной
системе отсчета. Он описывает абсолютное движение.
-
радиус-вектор, определяющий положение движущейся точки М в неподвижной
системе отсчета. Он описывает абсолютное движение.
3.2 Теоремы о схождении скоростей и ускорений
Скорости и ускорения точки в различных движениях будем определять как первую и вторую производные по времени от соответствующих радиусов-векторов.
1.
Относительную
скорость и относительное ускорение находим как первую и вторую производные по
времени от радиус-вектора ![]() , считая единичные орты
, считая единичные орты ![]() константами (в подвижной системе – они
постоянны).
константами (в подвижной системе – они
постоянны).
|
|
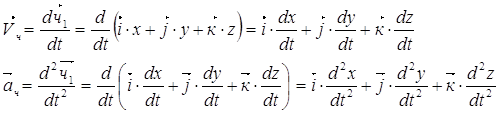
2.
Переносную
скорость и переносное ускорение находим как первую и вторую производные по
времени от радиус-вектора ![]() , считая координаты х/,
у/, z/
константами, а единичные орты – переменными.
, считая координаты х/,
у/, z/
константами, а единичные орты – переменными.
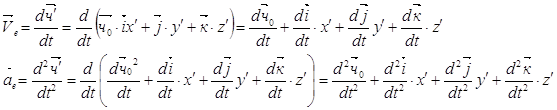
так как дифференцирование проведено, то мы можем воспользоваться равенствами (3.1), т.е. заменить х/ на х, у/ на у, z/ на z:
|
|
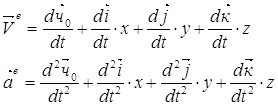
3.
Абсолютную
скорость и абсолютное ускорение находим как первую и вторую производные по
времени от радиус-вектора ![]() , считая все величины
переменными:
, считая все величины
переменными:
![]()
Таким образом доказана теорема сложения скоростей:
Абсолютная скорость равна геометрической сумме переносной и относительной скоростей.
![]() (3.6)
(3.6)
находим абсолютное ускорение:
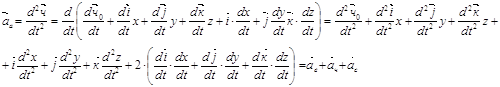
где введено обозначение:
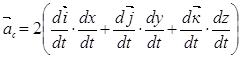 (3.7)
(3.7)
Величина ![]() , определяемая равенством (3.7) называется
поворотным ускорением или ускорением Кориолиса, по имени французского ученого,
доказавшего теорему сложения ускорений:
, определяемая равенством (3.7) называется
поворотным ускорением или ускорением Кориолиса, по имени французского ученого,
доказавшего теорему сложения ускорений:
Абсолютное ускорение точки равно геометрической сумме переносного, относительного и Кориолисов ускорений.
![]() (3.8)
(3.8)
3.3 Ускорение Кориолиса, его величина направление и физический смысл
Рассмотрим ускорение Кориолиса, определяемое равенством (3.7). Если подвижная система движется относительно неподвижной поступательно (т.е. переносное движение поступательное), то единичные орты будут постоянны и по модулю и по направлению и их производные по времени будут равны нулю, следовательно и ускорение Кориолиса равно нулю.
Теорема о сложении ускорений при поступательном переносном движении будет выражаться равенством:
![]()
![]() (3.9)
(3.9)
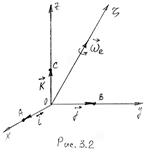
Рассмотрим переносное
вращательное движение. Пусть подвижная система вращается вокруг оси О3 с угловой
скоростью ![]() (рис. 3.2). единичные
орты
(рис. 3.2). единичные
орты ![]() можно рассматривать как радиус-векторы точек
А, В и С соответственно. А производные по времени от
радиус-векторов точек дают скорости точек.
можно рассматривать как радиус-векторы точек
А, В и С соответственно. А производные по времени от
радиус-векторов точек дают скорости точек.
|
Следовательно:
![]() ;
; ![]() ;
; ![]() (а)
(а)
с другой стороны, скорости точек А, В и С мы можем найти как во вращательном движении по формуле (2.11):
![]() ;
; ![]() ;
; ![]() (б)
(б)
сравнивая (а) и (б) находим, что:
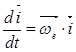 ;
; 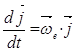 ;
; 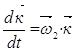 ; (в)
; (в)
Подставим эти значения в формулу (3.7)
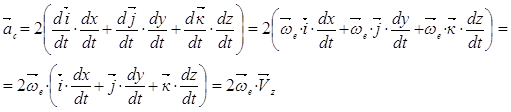
Таким образом ускорение Кориолиса равно удвоенному векторному произведению вектора угловой скорости переносного движения на вектор относительной скорости.
![]() (3.10)
(3.10)
Его величина
![]() (3.11)
(3.11)
|
В соответствии с правилом
векторного произведения ускорения Кориолиса направлено перпендикулярно
плоскости, в которой лежат векторы ![]() и
и ![]() ,
в ту сторону, чтобы, глядя навстречу ему, мы видим поворот вектора
,
в ту сторону, чтобы, глядя навстречу ему, мы видим поворот вектора ![]() к вектору
к вектору ![]() на
меньший угол происходящим против часовой стрелки.
на
меньший угол происходящим против часовой стрелки.
Другое правило: чтобы
найти направление ускорения Кориолиса, надо вектор ![]() спроецировать
на плоскость, перпендикулярно оси переносного вращения, и полученную проекцию
повернуть на 90о в сторону вращения. Эти и будет направление вектора
спроецировать
на плоскость, перпендикулярно оси переносного вращения, и полученную проекцию
повернуть на 90о в сторону вращения. Эти и будет направление вектора
![]() .
.
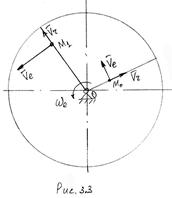
Физический смысл
ускорения Кориолиса выясним на таком примере. Пусть круглая платформа вращается
с постоянной угловой скоростью ![]() , а по радиусу платформы
двигается точка М с постоянной относительной скоростью Vч (рис. 3.3). В некоторый момент точка занимает
положение Мо, а через промежуток времени
, а по радиусу платформы
двигается точка М с постоянной относительной скоростью Vч (рис. 3.3). В некоторый момент точка занимает
положение Мо, а через промежуток времени ![]() положение М1. При этом произошло
изменение относительной скорости за счет переносного движения (изменилось
направление вектора
положение М1. При этом произошло
изменение относительной скорости за счет переносного движения (изменилось
направление вектора ![]() ) и изменение переносной скорости
за счет относительного движения (изменилась величина
) и изменение переносной скорости
за счет относительного движения (изменилась величина ![]() в
результате удаления точки от оси вращения). Эти два изменения и характеризуются
ускорением Кориолиса.
в
результате удаления точки от оси вращения). Эти два изменения и характеризуются
ускорением Кориолиса.
Таким образом, ускорение Кориолиса характеризует изменение относительной скорости в результате переносного движения и изменение переносной скорости в результате относительного движения.
В общем случае движения формулы (3.8) удобнее использовать в таком виде:
![]() (3.12)
(3.12)
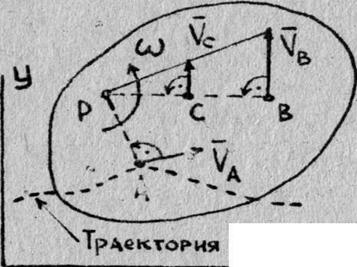
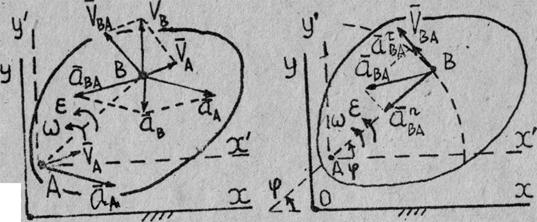
Задача кинематики плоского движения твердого тела - найти характеристики движения самого тела и отдельных его точек. В данном задании к таким характеристикам относятся векторы угловой скорости и углового ускорения тела.
![]() Рис.
1
Рис.
1
Основные формулы кинематики плоского движения твердого тела - векторные формулы, связывающие соответственно скорости и ускорения двух произвольных точек плоской фигуры, например, точек А и В (рис. 1)
![]() B =
B = ![]() A +
A + ![]() BA =
BA = ![]() A +
A + ![]() ´
´ ![]() ; (1)
; (1)
![]() B =
B = ![]() A +
A + ![]() +
+ ![]() =
= ![]() A +
A + ![]() × (
× (![]() ´
´ ![]() )
+
)
+ ![]() ×
× ![]() ; (2)
; (2)
где ![]() ,
, ![]() , - векторы угловой
скорости и углового ускорения вращения плоской фигуры вокруг любой оси,
например Az' перпендикулярной плоскости движения Oxy относительно системы
координат Ax'y'z', оси которой
параллельны осям неподвижной системы координат Оxyz.На рис.1 оси Оz. и Аz' не изображены, так как
считается, что они перпендикулярны к плоскости рисунка и направлены на
наблюдателя, а плоскости Охy и Аx'y' совпадают с плоскостью рисунка.
, - векторы угловой
скорости и углового ускорения вращения плоской фигуры вокруг любой оси,
например Az' перпендикулярной плоскости движения Oxy относительно системы
координат Ax'y'z', оси которой
параллельны осям неподвижной системы координат Оxyz.На рис.1 оси Оz. и Аz' не изображены, так как
считается, что они перпендикулярны к плоскости рисунка и направлены на
наблюдателя, а плоскости Охy и Аx'y' совпадают с плоскостью рисунка.
Левые части выражений
![]() BA =
BA = ![]() ´
´ ![]() ;
; ![]() =
= ![]() ×
(
×
(![]() ´
´ ![]() )
=
)
= ![]() ×
× ![]() BA;
BA; ![]() =
= ![]() ×
× ![]() ;
;
являются соответственно векторами скорости, нормального и касательного ускорения точки В
относительно системы координат Ax'y'z' при вращении отрезка АВ в плоскости рисунка вокруг точки A, называемой в таком
случае полюсом, с угловой скоростью ![]() и угловым ускорением
и угловым ускорением ![]() . Индексы n и t, в выражениях
. Индексы n и t, в выражениях ![]() и
и ![]() указывают, что эти
векторы направлены соответственно по внутренней нормали и касательной в точке B к окружности радиуса r = AB с центром в точке А.
Модули упомянутых векторов
указывают, что эти
векторы направлены соответственно по внутренней нормали и касательной в точке B к окружности радиуса r = AB с центром в точке А.
Модули упомянутых векторов ![]()
![]() находятся по формулам
находятся по формулам
½![]() BA½ =
BA½ = ![]() ´ AB; ½
´ AB; ½![]() ½ =
½ = ![]() =
= ![]() ´ AB; ½
´ AB; ½![]() ½ =
½ = ![]() ´ AB; (3)
´ AB; (3)
Векторы ![]() BA,
BA, ![]() ,
, ![]() лежат в плоскости
движения плоской фигуры тела, причем ненулевые векторы
лежат в плоскости
движения плоской фигуры тела, причем ненулевые векторы ![]() BA,
BA, ![]() перпендикулярны отрезку AB, а ненулевой вектор
перпендикулярны отрезку AB, а ненулевой вектор ![]() направлен от точки В к
точке А . Таким образом, для этих векторов всегда известны линии действия.
направлен от точки В к
точке А . Таким образом, для этих векторов всегда известны линии действия.
Поскольку модуль ускорения ![]() может быть вычислен по формуле (3) через угловую скорость тела
может быть вычислен по формуле (3) через угловую скорость тела ![]() , обычно известную к этапу нахождения
ускорений, целесообразно в формуле (2) вектор
, обычно известную к этапу нахождения
ускорений, целесообразно в формуле (2) вектор ![]() записывать вслед за
известным вектором
записывать вслед за
известным вектором ![]() А, т.е. перед вектором
А, т.е. перед вектором ![]() .
.
Векторы ![]() и
и ![]() параллельны
оси Оz
и поэтому полностью определяются своими проекциями на эту ось
параллельны
оси Оz
и поэтому полностью определяются своими проекциями на эту ось
Модуль проекции равен модулю вектора ![]() ;
; ![]() ,
а знак проекции указывает на направление вектора. Например, если проекции
векторов положительны (
,
а знак проекции указывает на направление вектора. Например, если проекции
векторов положительны (![]() , то векторы
, то векторы ![]() направлены так же, как и
направлены так же, как и ![]() , или ось Oz. Таким образом, при
плоском движении тела задача нахождения векторов
, или ось Oz. Таким образом, при
плоском движении тела задача нахождения векторов ![]() сводится
к задаче отыскания их проекций на ось Oz или Az'.
сводится
к задаче отыскания их проекций на ось Oz или Az'.
Если ![]() (рад) - угол между осью Ax' (Ох) и вектором
(рад) - угол между осью Ax' (Ох) и вектором ![]() (рис. 1) и за положительное направление
отсчета угла
(рис. 1) и за положительное направление
отсчета угла ![]() для выбранной системы координат принято
направление против хода часовой стрелки, то
для выбранной системы координат принято
направление против хода часовой стрелки, то
![]()
![]() рад/с;
рад/с; ![]() =
= ![]()
![]() =
= ![]()
![]() рад/с. (4)
рад/с. (4)
О направлении векторов ![]() и
и ![]() судят
по круговым стрелкам
судят
по круговым стрелкам ![]() и
и ![]() согласно правилу:
"круговая стрелка, направленная против хода стрелки часов, соответствует
вектору, направленному так же, как ось Oz".
согласно правилу:
"круговая стрелка, направленная против хода стрелки часов, соответствует
вектору, направленному так же, как ось Oz".
Из формул, использующих понятие МЦС (точка Р) на рис.2,
![]() ´
´ ![]() ;
; ![]() B =
B = ![]() ;
; ![]() ;
;
![]() ;
; ![]() , (5)
, (5)
следует, что в данный момент времени распределение скоростей точек
тела при плоском движении таково, как если бы тело вращалось вокруг оси Рz с угловой скоростью ![]() .
.
|
|
![]()
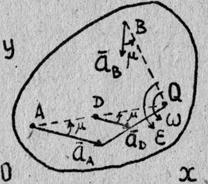
![]()
![]() Если отсчитывать угол 90 от направления
вектора скорости точки
Если отсчитывать угол 90 от направления
вектора скорости точки ![]() A к направлению АР от этой
точки до МЦС, то направление отсчета угла совпадает с направлением круговой стрелки
A к направлению АР от этой
точки до МЦС, то направление отсчета угла совпадает с направлением круговой стрелки ![]() . Этот
факт можно использовать для определения направления вектора
. Этот
факт можно использовать для определения направления вектора ![]() .
.
Из формул, использующих понятие МЦУ (точка Q на рис. 3),
![]()
![]() ;
; ![]()
![]() ; (6)
; (6)
![]() ,
,
следует, что в данный момент времени распределение ускорений точек
тела при плоском движении таково, как если бы тело вращалось вокруг оси Qz с угловой скоростью ![]() и угловым ускорением
и угловым ускорением ![]() .
.
Угол ![]() отсчитывается от вектора
ускорения какой-либо точки в направлении
круговой стрелки
отсчитывается от вектора
ускорения какой-либо точки в направлении
круговой стрелки ![]() . При отыскании положения МЦУ по
ускорениям двух точек, например по
. При отыскании положения МЦУ по
ускорениям двух точек, например по ![]() и
и ![]() , под углом
, под углом ![]() к
соответствующим ускорениям проводят лучи AQ и BQ. Точка пересечения лучей
(точка Q)
является МЦУ плоской фигуры в данный момент времени.
к
соответствующим ускорениям проводят лучи AQ и BQ. Точка пересечения лучей
(точка Q)
является МЦУ плоской фигуры в данный момент времени.
Направления векторов ![]() и
и ![]() помимо формул (4) могут быть найдены из
отдельных векторных формул
помимо формул (4) могут быть найдены из
отдельных векторных формул
![]() ;
; ![]() ;
; ![]() . (7)
. (7)
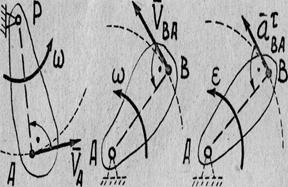
Рис. 4
Чтобы избежать анализа расположения трех взаимно перпендикулярных
векторов формул (7) при известных ![]() ,
, ![]() ,
,
![]() направления
направления ![]() и
и ![]() находят аналогично случаю вращательного
движения тела вокруг неподвижной оси (рис. 4).
находят аналогично случаю вращательного
движения тела вокруг неподвижной оси (рис. 4).
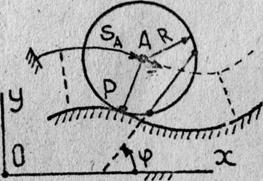
Рис. 5![]()
Кинематика плоского движения
катка радиуса R. при отсутствии скольжения по направляющей (в общем случае криволинейной), имеет некоторые особенности вследствие того, что мгновенный центр скоростей катка (точка Р ) совпадает с точкой окружности касающейся направляющей (рис. 5). Поэтому при движении катка расстояние от его центра (точки А) до МЦС является неизменным во времени и равным R.
AP(t) = const = R (8)
Свойство неизменности расстояния АР позволяет установить дополнительные соотношения, удобные для расчетов кинематических характеристик катка. Представим вектор скорости точки А с помощью:
а) формулы естественного способа задания движения точки
![]() , где
, где ![]() - единичный вектор
естественного трехгранника, касательный в точке A к кривой ее движения; SA - криволинейная
координата точки;
- единичный вектор
естественного трехгранника, касательный в точке A к кривой ее движения; SA - криволинейная
координата точки;
б) формулы (7) плоского движения тела
![]() ,
,
![]() ;
;
![]() - орт оси Оz, перпендикулярной
плоскости движения катка Qxy; j - угол, задающий
направление какого-либо отрезка плоской фигуры катка. Ввиду произвольности
выбора такого отрезка, обычно собственно отрезок, не указывают на рисунках, а
изображают лишь круговую стрелку положительного направления отсчета угла j, называя его углом
поворота катка.
- орт оси Оz, перпендикулярной
плоскости движения катка Qxy; j - угол, задающий
направление какого-либо отрезка плоской фигуры катка. Ввиду произвольности
выбора такого отрезка, обычно собственно отрезок, не указывают на рисунках, а
изображают лишь круговую стрелку положительного направления отсчета угла j, называя его углом
поворота катка.
Приравнивая правые части последних формул, имеем
![]() .
.
Поскольку вектoр ![]() коллинеарен результату векторного
произведения
коллинеарен результату векторного
произведения
![]() (
(![]() ^
^![]() ,
,
![]() ^
^![]() ),
то
),
то
![]() .
.
Откуда, используя свойство (8), получим формулы
![]() , или
, или ![]() , (9)
, (9)
справедливые для любого момента времени t.
В правой части формулы (9) берется знак "+", если при мысленном увеличении угла поворота катка j в направлении против хода стрелки часов наблюдается возрастание координаты SА центра движущегося катка в положительном направлении ее отсчета, иначе берется знак "-".
Так, например, для случая отсчетов SА и j, изображенном на рис.5, в формуле (9) необходимо брать знак "-".
Дифференцируя и интегрируя по времени соотношения (9), придем к выражениям
![]() , или
, или ![]() , (10),
, (10),
а также ![]() ,
,
где С - некоторая константа, значение которой зависит от выбора начал отсчетов SА и j. Обычно принимают С=0, так как считают, что когда SА=0, j также равно нулю. Из произведения соответствующих частей формул (9), (10),
![]() (11)
(11)
![]()
![]()
![]()
![]()
![]()
![]() следует, что если векторы
следует, что если векторы ![]() ,
, ![]() сонаправлены, то сонаправлены и векторы
сонаправлены, то сонаправлены и векторы ![]() ,
, ![]() .
.
Таким образом, с помощью формул (1-4), (8-9) могут быть найдены характеристики векторов скоростей и ускорений точек, векторов угловых скоростей и ускорений звеньев механизма, а с помощью формул (5, 6), (11) осуществлена их проверка.
Нахождение кинематических характеристик движения (![]() ,
, ![]() ,
, ![]() ,
,
![]() ) при помощи векторных формул (1), (2)
рекомендуется проводить следующим образом:
) при помощи векторных формул (1), (2)
рекомендуется проводить следующим образом:
1) написать формулу (1) или (2) применительно к конкретным точкам рассматриваемого звена механизма. При этом в качестве полюса следует взять точку с известными кинематическими характеристиками движения;
2) установить, известны или неизвестны на данном этапе решения две независимые характеристики {проекции на две оси или модуль и направляющий угол) для каждого вектора, входящего в уравнение (1) или (2). Найти значения тех независимых характеристик векторов, которые могут быть установлены из условий движения звена без решения рассматриваемого векторного уравнения;
3) решить векторное уравнение графоаналитическим или аналитическим методом (метод проекций).
© 2009 База Рефератов