Дипломная работа: Массивно-параллельные суперкомпьютеры серии Cry T3 и кластерные системы класса BEOWULF

Дипломная работа: Массивно-параллельные суперкомпьютеры серии Cry T3 и кластерные системы класса BEOWULF

Дипломная работа

по дисциплине: Параллельное программирование и параллельные вычисления

на тему: Массивно-параллельные суперкомпьютеры серии Cry T3 и кластерные системы класса BEOWULF

Реферат

Курсовой проект содержит 38 страниц машинописного текста, 11 литературных источников, 12 рисунков.

Ключевые слова: суперкомпьютер, архитектура, процессор, кластер, интерфейс, технология, операнд, компиляция, команда, оптимизация, переменная, данные, регистр, операция, итерационность, конвейерность, электронно-вычислительная машина.

В данном курсовом проекте рассматриваются многопроцессорные вычислительные системы Cry T3D(E) и Беовульф-кластеры рабочих станций, а также в все сопутствующие этим двум темам понятия и определения необходимые для понятного изложения материала.

Содержание

Введение

Основные понятия

1. Общие вопросы решения "больших задач"

1.1 Современные задачи науки и техники, требующие для решения суперкомпьютерных мощностей

1.2 Параллельная обработка данных

1.2.1 Принципиальная возможность параллельной обработки

1.2.2 Абстрактные модели параллельных вычислений

1.2.3 Способы параллельной обработки данных, погрешность вычислений

1.3 Понятие параллельного процесса и гранулы распараллеливания

1.4 Взаимодействие параллельных процессов, синхронизация процессов

1.5 Возможное ускорение при параллельных вычислениях (закон Амдаля)

2. Принципы построения многопроцессорных вычислительных систем

2.1 Архитектура многопроцессорных вычислительных систем

2.2 Распределение вычислений и данных в многопроцессорных вычислительных системах с распределенной памятью

2.3 Классификация параллельных вычислительных систем

2.4 Многопроцессорные вычислительные системы c распределенной памятью

2.4.1 Массивно-параллельные суперкомпьютеры серии Cry T3

2.4.2 Кластерные системы класса BEOWULF

2.4.3 Коммуникационные технологии, используемые при создании массово-параллельных суперкомпьютеров

Заключение

Список используемой литературы

Введение

Еще на заре компьютерной эры, примерно в середине прошлого века, конструкторы электронно-вычислительных машин задумались над возможностью применения параллельных вычислений в компьютерах. Ведь увеличение быстродействия только за счет совершенствования электронных компонентов компьютера – достаточно дорогой способ, который, к тому же, сталкивается с ограничениями, налагаемыми физическими законами. Так параллельная обработка данных и параллелизм команд были введены в конструкцию компьютеров и сейчас любой пользователь "персоналки", возможно, сам того не зная, работает на параллельном компьютере.

Одной из заметных тенденций развития человечества является желание максимально строго моделировать процессы окружающей действительности с целью как улучшения условий жизни в настоящем, так и максимально достоверного предсказания будущего. Математические методы и приемы цифрового моделирования во многих случаях позволяют разрешать подобные проблемы, однако с течением времени имеет место серьезное качественное и количественное усложнение технологии решения задач. Во многих случаях ограничением является недостаток вычислительных мощностей современных электронно-вычислительных машинах, но значимость решаемых задач привлекли огромные финансовые ресурсы в область создания сверхсложных электронно-вычислительных машин.

С некоторых пор повышение быстродействия компьютеров традиционной (именуемой "фон Неймановской") архитектуры стало чрезмерно дорого вследствие технологических ограничений при производстве процессоров, поэтому разработчики обратили внимание на иной путь повышения производительности – объединение электронно-вычислительных машин в многопроцессорные вычислительные системы. При этом отдельные фрагменты программы параллельно (и одновременно) выполняются на различных процессорах, обмениваясь информацией посредством внутренней компьютерной сети.

Идея объединения электронно-вычислительных машин с целью повышения, как производительности, так и надежности известны с конца пятидесятых годов.

Требования получить максимум производительности при минимальной стоимости привели к разработке многопроцессорных вычислительных комплексов; известны системы такого рода, объединяющие вычислительные мощности тысяч отдельных процессоров. Следующим этапом являются попытки объединить миллионы разнородных компьютеров планеты в единый вычислительный комплекс с огромной производительностью посредством сети Internet. На сегодняшний день применение параллельных вычислительных систем является стратегическим направлением развития вычислительной техники. Развитие "железа" с необходимостью подкрепляются совершенствованием алгоритмической и программной компонент – технологий параллельного программирования.

Метод распараллеливания вычислений существует уже давно, организация совместного функционирования множества независимых процессоров требует проведения серьезных теоретико-практических исследований, без которых сложная и относительно дорогостоящая многопроцессорная установка часто не только не превосходит, а уступает по производительности традиционному компьютеру.

Потенциальная возможность распараллеливания неодинакова для вычислительных задач различного типа – она значительна для научных программ, содержащих много циклов и длительных вычислений и существенно меньше для инженерных задач, для которых характерен расчет по эмпирическим формулам.

В данном курсовом проекте рассматриваются две основные темы:

1.         Многопроцессорные вычислительные системы (массивно-параллельные суперкомпьютеры) Cray T3D(E) с количеством процессоров от 40 до 2176. Это суперкомпьютеры с распределенной памятью на RISC-процессорах типа Alpha21164A, с топологией коммуникационной сети – трехмерный тор, операционной системой UNIX с микроядром и трансляторами для языков FORTRAN, HPF, C/C++. Поддерживаемые модели программирования: MPI, PVM, HPF.

2.         Беовульф-кластеры рабочих станций. Кластеры рабочих станций – совокупность рабочих станций, соединенных в локальную сеть. Кластер – вычислительная система с распределенной памятью и распределенным управлением. Кластерная система может обладать производительностью, сравнимой с производительностью суперкомпьютеров. Кластеры рабочих станций обычно называют Беовульф-кластерами (Beowulf cluster – по одноименному проекту), связанны локальной сетью Ethernet и используют операционную систему Linux.

Также в данном курсовом проекте рассматриваются все сопутствующие этим двум темам понятия и определения необходимые для понятного изложения материала.

Основные понятия

Наиболее распространенной технологией программирования для кластерных систем и параллельных компьютеров с распределенной памятью в настоящее время является технология MPI. Основным способом взаимодействия параллельных процессов в таких системах является передача сообщений друг другу. Это и отражено в названии данной технологии – Message Passing Interface (интерфейс передачи сообщений). Стандарт MPI фиксирует интерфейс, который должен соблюдаться как системой программирования на каждой вычислительной платформе, так и пользователем при создании своих программ. MPI поддерживает работу с языками Фортран и Си. Полная версия интерфейса содержит описание более 125 процедур и функций.

Интерфейс MPI поддерживает создание параллельных программ в стиле MIMD (Multiple Instruction Multiple Data), что подразумевает объединение процессов с различными исходными текстами. Однако писать и отлаживать такие программы очень сложно, поэтому на практике программисты, гораздо чаще используют SPMD-моделъ (Single Program Multiple Data) параллельного программирования, в рамках которой для всех параллельных процессов используется один и тот же код. В настоящее время все больше и больше реализаций MPI поддерживают работу с так называемыми "нитями".

Поскольку MPI является библиотекой, то при компиляции программы необходимо прилинковать соответствующие библиотечные модули.

После получения выполнимого файла необходимо запустить его на требуемом количестве процессоров.

После запуска одна и та же программа будет выполняться всеми запущенными процессами, результат выполнения в зависимости от системы будет выдаваться на терминал или записываться в файл.

MPI программа это множество параллельных взаимодействующих процессов. Все процессы порождаются один раз, образуя параллельную часть программы. В ходе выполнения MPI-программы порождение дополнительных процессов или уничтожение существующих не допускается (в дальнейших версиях MPI такая возможность появилась). Каждый процесс работает в своем адресном пространстве, никаких общих переменных или данных в MPI нет. Основным способом взаимодействия между процессами является явная посылка сообщений.

Для локализации взаимодействия параллельных процессов программы можно создавать группы процессов, предоставляя им отдельную среду для общения – коммуникатор. Состав образуемых групп произволен. Группы могут полностью совпадать, входить одна в другую, не пересекаться или пересекаться частично. Процессы могут взаимодействовать только внутри некоторого коммуникатора, сообщения, отправленные в разных коммуникаторах, не пересекаются и не мешают друг другу. Коммуникаторы имеют в языке Фортран тип integer (в языке Си – предопределенный тип MPI Comm).

При старте программы всегда считается, что все порожденные процессы работают в рамках всеобъемлющего коммуникатора. Этот коммуникатор существует всегда и служит для взаимодействия всех запущенных процессов MPI-программы. Все взаимодействия процессов протекают в рамках определенного коммуникатора, сообщения, переданные в разных коммуникаторах, никак не мешают друг другу.

Процессоры с сокращенным набором команд (RISC). В основе RISC-архитектуры (RISC – Reduced Instruction Set Computer) процессора лежит идея увеличения скорости его работы за счет упрощения набора команд.

Исследования показали, что 33% команд типичной программы составляют пересылки данных, 20% – условные ветвления и еще 16% арифметические и логические операции. В подавляющем большинстве команд вычисление адреса может быть выполнено быстро, за один цикл. Более сложные режимы адресации используются примерно в 18% случаев. Около 75% операндов являются скалярными, то есть переменными целого, вещественного, символьного типа и т. д., а остальные являются массивами и структурами. 80% скалярных переменных – локальные, а 90% структурных являются глобальными. Таким образом, большинство операндов – это локальные операнды скалярных типов. Они могут храниться в регистрах.

Согласно статистике, большая часть времени тратится на обработку операторов "вызов подпрограммы" и "возврат из подпрограммы". При компиляции эти операторы порождают длинные последовательности машинных команд с большим числом обращений к памяти, поэтому даже если доля этих операторов составляет всего 15%, они потребляют основную часть процессорного времени. Только около 1% подпрограмм имеют более шести параметров, а около 7% подпрограмм содержат более шести локальных переменных.

В результате изучения этой статистики был сделан вывод о том, что в типичной программе доминируют простые операции: арифметические, логические и пересылки данных. Доминируют и простые режимы адресации. Большая часть операндов – это скалярные локальные переменные. Одним из важнейших ресурсов повышения производительности является оптимизация указанных операторов.

В основу RISC-архитектуры положены следующие принципы и идеи. Набор команд должен быть ограниченным и включать только простые команды, время выполнения которых после выборки и декодирования один такт или чуть больше. Используется конвейерная обработка. Простые RISC-команды допускают эффективную аппаратную реализацию, в то время как сложные команды могут быть реализованы только средствами микропрограммирования. Конструкция устройства управления в случае RISC-архитектуры упрощается, и это дает возможность процессору работать на больших тактовых частотах. Использование простых команд позволяет эффективно реализовать и конвейерную обработку данных, и выполнение команд.

Сложные команды RISC-процессором выполняются дольше, но их количество относительно невелико. В RISC-процессорах небольшое число команд адресуется к памяти. Выборка данных из оперативной памяти требует более одного такта. Большая часть команд работает с операндами, находящимися в регистрах. Все команды имеют унифицированный формат и фиксированную длину. Это упрощает и ускоряет загрузку и декодирование команд, поскольку, например, код операции и поле адреса всегда находятся в одной и той же позиции. Переменные и промежуточные результаты вычислений могут храниться в регистрах. С учетом статистики использования переменных, большую часть локальных переменных и параметров процедур можно разместить в регистрах. При вызове новой процедуры содержимое регистров обычно перемещается в оперативную память, однако, если количество регистров достаточно велико, удается избежать значительной части длительных операций обмена с памятью, заменив их операциями с регистрами. Благодаря упрощенной архитектуре RISC-процессора, на микросхеме появляется место для размещения дополнительного набора регистров.

В настоящее время вычислительные системы с RISC-архитектурой занимают лидирующие позиции на мировом компьютерном рынке рабочих станций и серверов. Развитие RISC-архитектуры связано с развитием компиляторов, которые должны эффективно использовать преимущества большого регистрового файла, конвейеризации и т. д.

1. Общие вопросы решения "больших задач"

Под термином "большие задачи" обычно понимают проблемы, решение которых требует не только построения сложных математических моделей, но и проведения огромного, на многие порядки превышающие характерные для программируемых электронно-вычислительных машин, количества вычислений. Здесь применяют с соответствующими ресурсами электронно-вычислительные машины – размерами оперативной и внешней памяти, быстродействием линий передачи информации и др.

Верхний предел количества вычислений для "больших задач" определяется лишь производительностью существующих на данный момент вычислительных систем. При "прогонке" вычислительных задач в реальных условиях ставится не вопрос "решить задачу вообще", а "решить за приемлемое время" (часы/десятки часов).

1.1 Современные задачи науки и техники, требующие для решения суперкомпьютерных мощностей

Достаточно часто приходится сталкиваться с такими задачами, которые, представляя немалую ценность для общества, не могут быть решены с помощью относительно медленных компьютеров офисного или домашнего класса. Единственная надежда в этом случае возлагается на компьютеры с большим быстродействием, которые принято называть суперкомпьютерами. Только машины такого класса могут справиться с обработкой больших объемов информации. Это могут быть, например, статистические данные или результаты метеорологических наблюдений, финансовая информация. Иногда скорость обработки имеет решающее значение. В качестве примера можно привести составление прогноза погоды и моделирование климатических изменений. Чем раньше предсказано стихийное бедствие, тем больше возможностей подготовиться к нему. Важной задачей является моделирование лекарственных средств, расшифровка генома человека, томография, в том числе и медицинская, разведка месторождений нефти и газа. Примеров можно привести много.

Моделирование процессов окружающей действительности с целью как улучшения условий жизни в настоящем, так и достоверного предсказания будущего, является одной из тенденций развития человечества. Математические методы и приемы цифрового моделирования во многих случаях позволяют разрешать подобные проблемы, однако с течением времени имеет место усложнение технологии решения подобных задач. Во многих случаях ограничением является недостаток вычислительных мощностей современных электронно-вычислительных машин.

Требования получить максимум производительности при минимальной стоимости привели к разработке многопроцессорных вычислительных комплексов; известны системы такого рода, объединяющие вычислительные мощности тысяч отдельных процессоров.

Ниже перечислены некоторые области человеческой деятельности, требующие для своего решения суперкомпьютерных мощностей использующих параллельные вычисления:

v Предсказания погоды, климата и глобальных изменений в атмосфере

v Науки о материалах

v Построение полупроводниковых приборов

v Сверхпроводимость

v Разработка фармацевтических препаратов

v Генетика человека

v Астрономия

v Транспортные задачи большой размерности

v Гидро и газодинамика

v Управляемый термоядерный синтез

v Разведка нефти и газа

v Вычислительные задачи наук о мировом океане

v Распознавание и синтез речи, распознавание изображений

Одна из серьезнейших задач – моделирование климатической системы и предсказание погоды. При этом совместно численно решаются уравнения динамики сплошной среды и уравнения равновесной термодинамики. Для моделирования развития атмосферных процессов на протяжении 100 лет и числе элементов дискретизации 2,6×106 (сетка с шагом 10 по широте и долготе по всей поверхности Планеты при 20 слоях по высоте, состояние каждого элемента описывается 10 компонентами) в любой момент времени состояние земной атмосферы описывается 2,6×107 числами. При шаге дискретизации по времени 10 минут за моделируемый промежуток времени необходимо определить 5×104 ансамблей (то есть 1014 необходимых числовых значений промежуточных вычислений). При оценке числа необходимых для получения каждого промежуточного результата вычислительных операций в 102÷103 общее число необходимых для проведения численного эксперимента с глобальной моделью атмосферы вычислений с плавающей точкой доходит до 1016÷1017.

Суперкомпьютер с производительностью 1012 оп/сек при идеальном случае (полная загруженность и эффективная алгоритмизация) будет выполнять такой эксперимент в течение нескольких часов; для проведения полного процесса моделирования необходима многократная (десятки/сотни раз) прогонка программы.

Проблема супервычислений столь важна, что многие государства курируют работы в области суперкомпьютерных технологий.

Государственная поддержка прямо связана с тем, что независимость в области производства и использования вычислительной техники отвечает интересам национальной безопасности, а научный потенциал страны непосредственно связан и в большой мере определяется уровнем развития вычислительной техники и математического обеспечения.

С целью объективности при сравнении производительность супер-электронно-вычислительных машин рассчитывается на основе выполнения заранее известной тестовой задачи ("бенчмарка", от англ. benchmark). Пиковая производительность определяется максимальным числом операций, которое может быть выполнено за единичное время при отсутствии связей между функциональными устройствами, характеризует потенциальные возможности аппаратуры и не зависит от выполняемой программы.

Недостатком метода оценки пиковой производительности как числа выполняемых компьютером команд в единицу времени (MIPS, Million Instruction Per Second) дает только самое общее представление о быстродействии, так как не учитывает специфику конкретных программ (трудно предсказуемо, в какое число и каких именно инструкций процессора отобразится пользовательская программа).

Необходимо отметить, что существуют аргументы против широкого практического применения параллельных вычислений:

ü   Параллельные вычислительные системы чрезмерно дороги. По подтверждаемому практикой закону Гроша, производительность компьютера растет пропорционально квадрату его стоимости; в результате гораздо выгоднее получить требуемую вычислительную мощность приобретением одного производительного процессора, чем использование нескольких менее быстродействующих процессоров.

Контраргумент. Рост быстродействия последовательных электронно-вычислительных машин не может продолжаться бесконечно, компьютеры подвержены быстрому моральному старению и необходимы частые финансовые затраты на покупку новых моделей. Практика создания параллельных вычислительных систем класса Beowulf ясно показала экономичность именно этого пути.

ü   При организации параллелизма излишне быстро растут потери производительности. По гипотезе Минского (Marvin Minsky) достигаемое при использовании параллельной системы ускорение вычислений пропорционально двоичному логарифму от числа процессоров (при 1000 процессорах возможное ускорение оказывается равным всего 10).

Контраргумент. Приведенная оценка ускорения верна для распараллеливания определенных алгоритмов. Однако существует большое количество задач, при параллельном решении которых достигается близкое к 100% использованию всех имеющихся процессоров параллельной вычислительной системы.

ü   Последовательные компьютеры постоянно совершенствуются. По широко известному закону Мура сложность последовательных микропроцессоров возрастает вдвое каждые 18 месяцев, поэтому необходимая производительность может быть достигнута и на "обычных" последовательных компьютерах.

Контраргумент. Аналогичное развитие свойственно и параллельным системам.

ü   Однако применение параллелизма позволяет получать необходимое ускорение вычислений без ожидания разработки новых более быстродействующих процессоров. Эффективность параллелизма сильно зависит от характерных свойств параллельных систем. Все современные последовательные электронно-вычислительные машины работают в соответствие с классической схемой фон-Неймана; параллельные системы отличаются существенным разнообразием архитектуры и максимальный эффект от использования параллелизма может быть получен при полном использовании всех особенностей аппаратуры (следствие – перенос параллельных алгоритмов и программ между разными типами систем затруднителен, а иногда и невозможен).

Контраргумент. При реально имеющемся разнообразии архитектур параллельных систем существуют и определенные "устоявшиеся" способы обеспечения параллелизма. Инвариантность создаваемого программного обеспечения обеспечивается при помощи использования стандартных программных средств поддержки параллельных вычислений (программные библиотеки PVM, MPI, DVM и др.). PVM и MPI используются в суперкомпьютерах Cray-T3.

ü   За десятилетия эксплуатации последовательных электронно-вычислительных машинах накоплено огромное программное обеспечение, ориентировано на последовательные электронно-вычислительные машины; переработка его для параллельных компьютеров практически нереальна.

Контраргумент. Если эти программы обеспечивают решение поставленных задач, то их переработка вообще не нужна. Однако если последовательные программы не позволяют получать решение задач за приемлемое время или же возникает необходимость решения новых задач, то необходима разработка нового программного обеспечения и оно изначально может реализовываться в параллельном исполнении.

ü   Существует ограничение на ускорение вычисление при параллельной реализации алгоритма по сравнению с последовательной.

Контраргумент. В самом деле, алгоритмов вообще без (определенной) доли последовательных вычислений не существует. Однако это суть свойство алгоритма и не имеет отношения к возможности параллельного решения задачи вообще. Необходимо научиться применять новые алгоритмы, более подходящие для решения задач на параллельных системах.

Таким образом, на каждое критическое соображение против использования параллельных вычислительных технологий находится более или менее существенный контраргумент.

1.2 Параллельная обработка данных

1.2.1 Принципиальная возможность параллельной обработки

Практически все разработанные к настоящему времени алгоритмы являются последовательными. Например, при вычислении выражения a + b × c , сначала необходимо выполнить умножение и только потом выполнить сложение. Если в электронно-вычислительных машин присутствуют узлы сложения и умножения, которые могут работать одновременно, то в данном случае узел сложения будет простаивать в ожидании завершения работы узла умножения. Можно доказать утверждение, состоящее в том, что возможно построить машину, которая заданный алгоритм будет обрабатывать параллельно.

Можно построить m процессоров, которые при одновременной работе выдают нужный результат за один-единственный такт работы вычислителя.

Такие "многопроцессорные" машины теоретически можно построить для каждого конкретного алгоритма и, казалось бы, "обойти" последовательный характер алгоритмов. Однако не все так просто – конкретных алгоритмов бесконечно много, поэтому развитые выше абстрактные рассуждения имеют не столь прямое отношение к практической значимости. Их развитие убедило в самой возможности распараллеливания, явилось основой концепции неограниченного параллелизма, дало возможность рассматривать с общих позиций реализацию так называемых вычислительных сред – многопроцессорных систем, динамически настраиваемых под конкретный алгоритм.

1.2.2 Абстрактные модели параллельных вычислений

Модель параллельных вычислений обеспечивает высокоуровневый подход к определению характеристик и сравнению времени выполнения различных программ, при этом абстрагируются от аппаратного обеспечения и деталей выполнения. Первой важной моделью параллельных вычислений явилась машина с параллельным случайным доступом (PRAM – Parallel Random Access Machine), которая обеспечивает абстракцию машины с разделяемой памятью (PRAM является расширением модели последовательной машины с произвольным доступом RAM – Random Access Machine). Модель BSP (Bulk Synchronous Parallel, массовая синхронная параллельная) объединяет абстракции как разделенной, так и распределенной памяти. Считается, что все процессоры выполняют команды синхронно; в случае выполнения одной и той же команды PRAM является абстрактной SIMD-машиной, (SIMD – Single Instruction stream/Multiple Data stream – одиночный поток команд наряду со множественным потоком данных), однако процессоры могут выполнять и различные команды. Основными командами являются считывание из памяти, запись в память и обычные логические и арифметические операции.

Модель PRAM идеализирована в том смысле, что каждый процессор в любой момент времени может иметь доступ к любой ячейке памяти (Операции записи, выполняемые одним процессором, видны всем остальным процессорам в том порядке, в каком они выполнялись, но операции записи, выполняемые разными процессорами, могут быть видны в произвольном порядке). Например, каждый процессор в PRAM может считывать данные из ячейки памяти или записывать данные в эту же ячейку. На реальных параллельных машинах такого, конечно, не бывает, поскольку модули памяти на физическом уровне упорядочивают доступ к одной и той же ячейке памяти. Более того, время доступа к памяти на реальных машинах неодинаково из-за наличия кэшей и возможной иерархической организации модулей памяти.

Базовая модель PRAM поддерживает конкурентные (в данном контексте параллельные) считывание и запись. Известны подмодели PRAM, учитывающие правила, позволяющие избежать конфликтных ситуаций при одновременном обращении нескольких процессоров к общей памяти.

Моделировать схемы из функциональных элементов с помощью параллельных машин с произвольным доступом (PRAM) позволяет теорема Брента. В качестве функциональных элементов могут выступать как 4 основных (осуществляющих логические операции NOT, AND, OR, XOR – отрицание, логическое И, логическое ИЛИ и исключающее ИЛИ соответственно), более сложные NAND и NOR (И-НЕ и ИЛИ-НЕ), так и любой сложности.

В дальнейшем предполагается, что задержка (т.е. время срабатывания время, через которое предусмотренные значения сигналов появляются на выходе элемента после установления значений на входах) одинакова для всех функциональных элементов.

Рассматривается схема из функциональных элементов, соединенных без образования циклов (предполагаем, что функциональные элементы имеют любое количество входов, но ровно один выход – элемент с несколькими выходами можно заменить несколькими элементами с единственным выходом). Число входов определяет входную степень элемента, а число входов, к которым подключен выход элемента – его выходной степенью. Обычно предполагается, что входные степени всех используемых элементов ограничены сверху, выходные же степени могут быть любыми. Под размером схемы понимается количество элементов в ней, наибольшее число элементов на путях от входов схемы к выходу элемента называется глубиной этого элемента (глубина схемы равна наибольшей из глубин составляющих ее элементов).

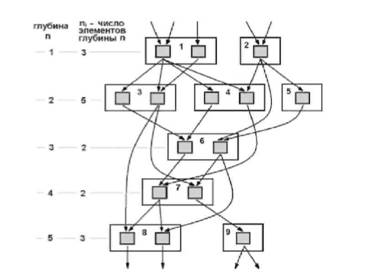
Рисунок 1. Моделирование схемы размера 15, глубины 5 с двумя процессорами с помощью параллельной машины с произвольным доступом (PRAM – машина)

На рисунке 1 приведен результат моделирования схемы размером (общее количество процессоров) n=15 при глубине схемы (максимальное число элементов на каждом из уровней глубины) d=5 с числом процессоров p=2 (одновременно моделируемые элементы объединены в группы прямоугольными областями, причем для каждой группы указан шаг, на котором моделируются ее элементы; моделирование происходит последовательно сверху вниз в порядке возрастания глубины, на каждой глубине по р штук за раз). Согласно теоремы Брента моделирование такой схемы займет не более ceil(15/2+1)=9 шагов.

1.2.3 Способы параллельной обработки данных, погрешность вычислений

Возможны следующие режимы выполнения независимых частей программы:

·          Параллельное выполнение – в один и тот же момент времени выполняется несколько команд обработки данных; этот режим вычислений может быть обеспечен не только наличием нескольких процессоров, но и с помощью конвейерных и векторных обрабатывающих устройств.

·          Распределенные вычисления – этот термин обычно применяют для указания способа параллельной обработки данных, при которой используются несколько обрабатывающих устройств, достаточно удаленных друг от друга и в которых передача данных по линиям связи приводит к существенным временным задержкам.

При таком способе организации вычислений эффективна обработка данных только для параллельных алгоритмов с низкой интенсивностью потоков межпроцессорных передач данных; таким образом функционируют, например, многомашинные вычислительные комплексы, образуемые объединением нескольких отдельных электронно-вычислительных машин с помощью каналов связи локальных или глобальных информационных сетей.

Формально к этому списку может быть отнесен и многозадачный режим (режим разделения времени), при котором для выполнения процессов используется единственный процессор; в этом режиме удобно отлаживать параллельные приложения.

Существует два способа параллельной обработки данных: параллелизм и конвейерность.

Параллелизм предполагает наличие p одинаковых устройств для обработки данных и алгоритм, позволяющий производить на каждом независимую часть вычислений, в конце обработки частичные данные собираются вместе для получения окончательного результата. В этом случае получим ускорение процесса в p раз. Далеко не каждый алгоритм может быть успешно распараллелен таким способом (естественным условием распараллеливания является вычисление независимых частей выходных данных по одинаковым – или сходным – процедурам; итерационность или рекурсивность вызывают наибольшие проблемы при распараллеливании).

Идея конвейерной обработки заключается в выделении отдельных этапов выполнения общей операции, причем каждый этап после выполнения своей работы передает результат следующему, одновременно принимая новую порцию входных данных. Каждый этап обработки выполняется своей частью устройства обработки данных (ступенью конвейера), каждая ступень выполняет определенное действие (микрооперацию); общая обработка данных требует срабатывания этих частей последовательно.

Конвейерность при выполнении команд имитирует работу конвейера сборочного завода, на котором изделие последовательно проходит ряд рабочих мест; причем на каждом из них над изделием производится новая операция. Эффект ускорения достигается за счет одновременной обработки ряда изделий на разных рабочих местах.

Ускорение вычислений достигается за счет использования всех ступеней конвейера для потоковой обработки данных (данные потоком поступают на вход конвейера и последовательно обрабатываются на всех ступенях). Конвейеры могут быть скалярными или векторными устройствами (разница состоит лишь в том, что в последнем случае могут быть использованы обрабатывающие векторы команды). В случае длины конвейера l время обработки n независимых операций составит l+n−1 (каждая ступень срабатывает за единицу времени). При использовании такого устройства для обработки единственной порции входных данных потребуется время l×n и только для множества порций получим ускорение вычислений, близкое к l.

Из рисунка 2 видно, что производительность E конвейерного устройства асимптотически растет с увеличением длины n набора данных на его входе, стремясь к теоретическому максимуму производительности 1/τ

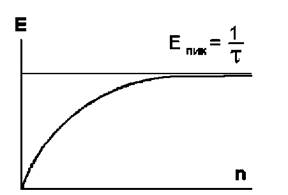
Рисунок 2. Производительность конвейерного устройства в функции длины входного набора данных

1.3 Понятие параллельного процесса и гранулы распараллеливания

Наиболее общая схема выполнения последовательных и параллельных вычислений приведена на рисунке 3 (моменты времени S и E – начало и конец задания соответственно).

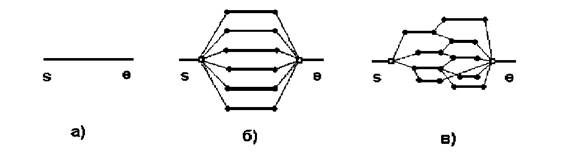
Рисунок 3. Диаграммы выполнения процессов при последовательном вычислении – а), при близком к идеальному распараллеливании б) и в общем случае распараллеливания – в)

Процессом называют определенные последовательности команд, наравне с другими процессами претендующие для своего выполнения на использование процессора; команды (инструкции) внутри процесса выполняются последовательно, внутренний параллелизм при этом не учитывают.

На рисунке 3 тонкими линиями показаны действия по созданию процессов и обмена данными между ними, толстыми – непосредственно исполнение процессов (ось абсцисс – время). В случае последовательных вычислений создается единственный процесс (рисунок 3a), осуществляющий необходимые действия; при параллельном выполнении алгоритма необходимы несколько процессов (параллельных ветвей задания). В идеальном случае все процессы создаются одновременно и одновременно завершаются (рисунок 3б), в общем случае диаграмма процессов значительно сложнее и представляет собой некоторый граф (рисунок 3в).

Характерная длина последовательно выполняющейся группы команд в каждом из параллельных процессов называется размером гранулы (зерна). В любом случае целесообразно стремиться к "крупнозернистости" (идеал – диаграмма 3б). Обычно размер зерна (гранулы) составляет десятки-сотни тысяч машинных операций (что на порядки превышает типичный размер оператора языков Fortran или C/C++). В зависимости от размеров гранул говорят о мелкозернистом и крупнозернистом параллелизме.

На размер гранулы влияет и удобство программирования – в виде гранулы часто оформляют некий логически законченный фрагмент программы. Целесообразно стремиться к равномерной загрузке процессоров.

Разработка параллельных программ является непростой задачей в связи с трудностью выявления параллелизма (обычно скрытого) в программе (то есть выявления частей алгоритма, могущих выполняться независимо друг от друга).

Автоматизация выявления параллелизма в алгоритмах непроста и в полном объеме вряд ли может быть решена в ближайшее время. В то же время за десятилетия эксплуатации вычислительной техники разработано такое количество последовательных алгоритмов, что не может быть и речи об их ручном распараллеливании.

Даже простейшая модель параллельных вычислений позволяет выявить важное обстоятельство – время обмена данными должно быть как можно меньше времени выполнения последовательности команд, образующих гранулу.

Для реальных задач (традиционно) характерный размер зерна распараллеливания на несколько порядков превышает характерный размер оператора традиционного языка программирования (C/C++ или Fortran).

1.4 Взаимодействие параллельных процессов, синхронизация процессов

Выполнение команд программы образует вычислительный процесс, в случае выполнения нескольких программ на общей или разделяемой памяти и обмене этих программ сообщениями принято говорить о системе совместно протекающих взаимодействующих процессов.

Порождение и уничтожение процессов UNIX-подобных операционных системах выполняются операторами (системными вызовами).

Параллелизм часто описывается в терминах макрооператоров, в параллельных языках запуск параллельных ветвей осуществляется с помощью оператора JOIN.

Для многопроцессорных вычислительных систем особое значение имеет обеспечение синхронизации процессов. Например, момент времени наступления обмена данными между процессорами априори никак не согласован и не может быть определен точно, так как зависит от множества труднооцениваемых параметров функционирования многопроцессорных вычислительных систем, при этом для обеспечения встречи для обмена информацией просто необходимо применять синхронизацию. В слабосвязанных многопроцессорных вычислительных системах вообще нельзя надеяться на абсолютную синхронизацию машинных часов отдельных процессоров, можно говорить только об измерении промежутков времени во временной системе каждого процессора.

Синхронизация является действенным способом предотвращения ситуаций "тупика" ситуации, когда каждый из взаимодействующих процессов получил в распоряжение часть необходимых ему ресурсов, но ни ему ни иным процессам этого количества ресурсов недостаточно для завершения обработки и последующего освобождения ресурсов.

В системах параллельного программирования используют высокоуровневые приемы синхронизации. В технологии параллельного программирования MPI применена схема синхронизации обмена информацией между процессами.

Синхронизация может поддерживаться и аппаратно (например, барьерная синхронизация в суперкомпьютере Cray T3, с помощью которой осуществляется ожидание всеми процессами определенной точки в программе, после достижения которой возможна дальнейшая работа.

1.5 Возможное ускорение при параллельных вычислениях (закон Амдаля)

Представляет интерес оценка величины возможного повышения производительности с учетом качественных характеристик самой исходно последовательной программы.

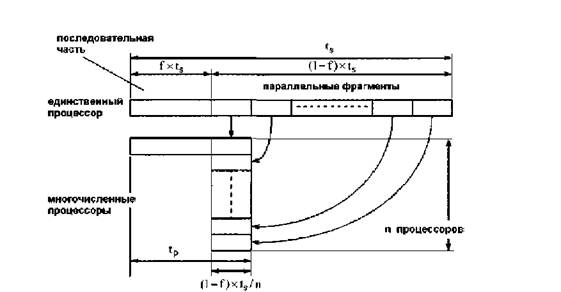
Рисунок 4. Схема к выводу закона Амдаля

Закон Амдаля (1967) связывает потенциальное ускорение вычислений при распараллеливании с долей операций, выполняемых априори последовательно. Пусть f (0<f<1) – часть операций алгоритма, которую распараллелить не представляется возможным; тогда распараллеливаемая часть равна (1-f); при этом затраты времени на передачу сообщений не учитываются, ts – время выполнения алгоритма на одном процессоре (последовательный вариант), n – число процессоров параллельной машины.

При переносе алгоритма на параллельную машину время расчета распределится так:

· f×ts – время выполнения части алгоритма, которую распараллелить невозможно,

· (1-f )×ts/n – время, затраченное на выполнение распараллеленной части алгоритма.

Время tp, необходимое для расчета на параллельной машине с n процессорами, равно

tp=f×ts+(1-f)×ts/n .

Ускорение времени расчета при малой доли последовательной операций (f<<1) возможно достичь (не более чем в n раз) ускорения вычислений (рисунок 4).

Рисунок 5. Трехмерный график, количественно отражающий зависимость Амдаля

В случае f=0,5 ни при каком количестве процессоров невозможно достичь S>2! Заметим, что эти ограничения носят фундаментальный характер (их нельзя обойти для заданного алгоритма), однако практическая оценка доли f последовательных операций априори обычно невозможна.

Таким образом, качественные характеристики самого алгоритма накладывают ограничения на возможное ускорение при распараллеливании. Например, характерные для инженерных расчетов алгоритмы счета по последовательным формулам распараллеливаются плохо (часть f значима), в то же время сводимые к задачам линейного программирования алгоритмы распараллеливаются удовлетворительно.

Априорно оценить долю последовательных операций f непросто. Однако можно попробовать формально использовать закон Амдаля для решения обратной задачи определения f по экспериментальным данным производительности; это дает возможность количественно судить о достигнутой эффективности распараллеливания.

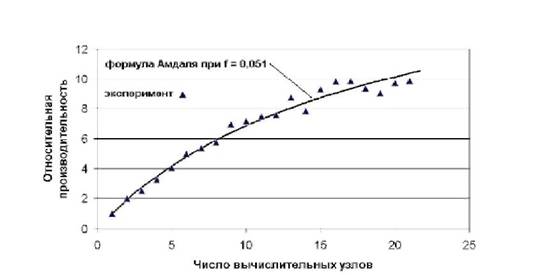
Рисунок 6. Производительность вычислительной кластерной системы на процедуре умножения матриц (эксперимент и расчет по формуле Амдаля)

На рисунке 6 приведены результаты эксперимента на кластере SCI-MAIN НИВЦ МГУ на задаче умножения матриц по ленточной схеме (размерность 103×103 вещественных чисел двойной точности), экспериментальные данные наилучшим образом (использован метод наименьших квадратов) соответствуют формуле Амдаля при f=0,051.

Закон Амдаля удобен для качественного анализа проблемы распараллеливания.

2. Принципы построения многопроцессорных вычислительных систем

2.1 Архитектура многопроцессорных вычислительных систем

Архитектура параллельных компьютеров развивалась практически с самого начала их создания и применения, причем в самых различных направлениях. Наиболее общие положения приводят к двум классам – компьютеры с общей памятью и компьютеры с распределенной памятью.

Компьютеры с общей памятью состоят из нескольких процессоров, имеющих равноприоритетный доступ к общей памяти с единым адресным пространством (рисунок 7a).

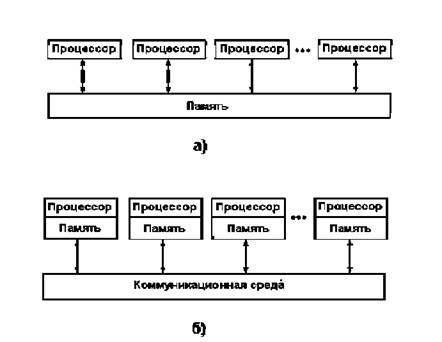
Рисунок 7. Параллельные компьютеры: с общей памятью – а) и с распределенной памятью – б)

Типичный пример такой архитектуры – компьютеры класса SMP (Symmetric Multi Processors), включающие несколько процессоров, но одну память, комплект устройств ввода/вывода и операционную систему. Достоинством компьютеров с общей памятью является относительная простота программирования параллельных задач, минусом недостаточная масштабируемость. Реальные SMP-системы содержат обычно не более 32 процессоров, для дальнейшего наращивания вычислительных мощностей подобных систем используется NUMA-технология.

В компьютерах с распределенной памятью (мультикомпьютерные системы) каждый вычислительный узел является полноценным компьютером и включает процессор, память, устройства ввода/вывода, операционную систему и др. (рисунок 7б). Типичный пример такой архитектуры – компьютерные системы класса MPP (Massively Parallel Processing), в которых с помощью некоторой коммуникационной среды объединяются однородные вычислительные узлы. Достоинством компьютеров с распределенной памятью является (почти неограниченная) масштабируемость, недостатками – необходимость применения специализированных программных средств (библиотек обмена сообщениями) для осуществления обменов информацией между вычислительными узлами. Для многопроцессорных вычислительных систем с общей и распределенной памятью используются термины сильно- и слабосвязанные машины соответственно.

Как было показано, производительность каналов обмена сильно влияет на возможность эффективного распараллеливания, причем это важно для обоих рассмотренных архитектур. Простейшей системой коммуникации является общая шина (рисунок 8a), которая связывает все процессоры и память, однако даже при числе устройств на шине больше нескольких десятков производительность шины катастрофически падает вследствие взаимного влияния и конкуренции устройств за монопольное владение шиной при обменах данными.

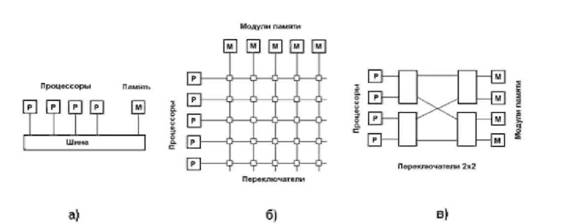
Рисунок 8. Многопроцессорные системы с общей шиной – а), с матричным коммутатором – б) и с каскадированием коммутаторов (Омега-сеть) – в)

При построении более мощных систем используются более изощренные подходы. Эффективной является схема матричной коммутации (рисунок 8б), при которой устройства связываются между собой двунаправленными переключателями, разрешающими или запрещающими передачу информации между соответствующими модулями. Альтернативой является каскадирование переключателей; например, по схеме Омега-сети (рисунок 8в). При этом каждый переключатель может соединять любой из двух своих входов с любым из двух выходов, для соединения n процессоров с n блоками памяти в этом случае требуется n×log2n/2 переключателей. Недостаток схем с каскадированием коммутаторов – задержки срабатывания переключателей.

Для систем с распределенной памятью используются практически все мыслимые варианты соединений (рисунок 9), при этом параметром качества с точки зрения скорости передачи сообщений служит величина средней длины пути, соединяющего произвольные процессоры; при этом имеется в виду именно физический путь, так как реализовать логическую топологию (программными средствами) не представляет трудностей.

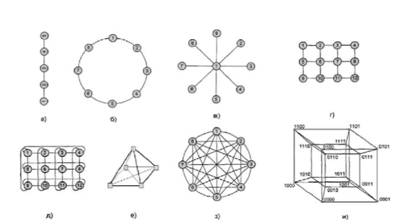
Рисунок 9. Варианты топологий связи процессоров в многопроцессорных вычислительных системах

Простейшая линейная топология (рисунок 9a) удовлетворительно соответствует многим алгоритмам, для которых характерна связь лишь соседних процессов между собой (одномерные задачи математической физики и многомерные, сводимые к одномерным); недостаток – невозможность передачи сообщений при разрыве в любом месте. Уменьшение вдвое средней длины пути и повышение надежности связи (при нарушении связи сообщения могут быть переданы в противоположном направлении, хотя и с меньшей скоростью) достигается соединение первого узла с последним – получается топология "кольцо" (рисунок 9б). Топология "звезда" (рисунок 9в) максимально отвечает распределению нагрузки между процессами, характерной для систем "клиент/сервер" (главный узел "раздает" задания и "собирает" результаты расчетов, при этом подчиненные узлы друг с другом взаимодействуют минимально).

Топология "решетка" (рисунок 9г) использовалась еще в начале девяностых годов при построении суперкомпьютера Intel Paragon на основе процессоров i860; нахождение минимального пути передачи данных между процессорами A и B для топологии "трехмерная решетка" иллюстрировано на рисунке 10. Топология "двумерный тор" (рисунок 9д) расширяет "двумерную решетку" дополнительными связями, снижающими длину среднего пути (само собой, возможен и "трехмерный тор") и характерна для сетевой технологии SCI. Применяется (рисунок 9e) характеризующаяся наличием связи каждого процессора с каждым трехмерная топология "клика". На рисунке 9з приведен общий вид топологии полной связи всех процессоров между собой; такая топология характеризуется наименьшей длиной среднего пути между процессорами, однако аппаратно практически нереализуема при значительном числе процессоров вследствие катастрофического роста числа связей. Для топологии "гиперкуб" (рисунок 9и) характерна сокращенная длина среднего пути и близость к структурам многих алгоритмов численных расчетов, что обеспечивает высокую производительность. N-мерный гиперкуб содержит 2N процессоров. Двухмерный гиперкуб – это квадрат, трехмерный гиперкуб образует обычный куб, а четырехмерный гиперкуб представляет собой куб в кубе. Для семейства суперкомпьютеров nCube гиперкуб максимальной размерности 13 содержит 8192 процессора, в системе nCube 3 число процессоров может достигать 65536 (16-мерный гиперкуб).

В качестве основных характеристик топологии сети передачи данных часто используются следующие показатели:

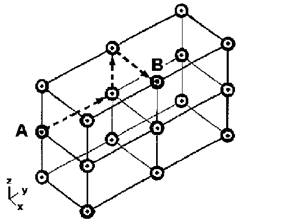
Рисунок 10. Нахождение минимального пути для передачи сообщений между процессорами в топологии "трехмерная решетка"

-          Диаметр определяется как максимальное расстояние (обычно кратчайших путь между процессорами) между двумя процессорами в сети, эта величина характеризует максимально необходимое время для передачи данных между процессорами (время передачи в первом приближении прямо пропорционально длине пути).

Связность – показатель, характеризующий наличие разных маршрутов передачи данных между процессорами сети; конкретный вид показателя может быть определен, например, как минимальное количество дуг, которое надо удалить для разделения сети передачи данных на две несвязные области.

-          Ширина бинарного деления – показатель, определяемый как минимальное количество дуг, которое надо удалить для разделения сети передачи данных на две несвязные области одинакового размера.

-          Стоимость определяется, например, как общее количество линий передачи данных в многопроцессорной вычислительной системе.

Естественным представляется объединение преимуществ систем с общей (относительная простота создания параллельных программ) и распределенной памятью (высокая масштабируемость); решением этого вопроса явилось создание компьютеров с архитектурой NUMA (Non Uniform Memory Access).

В этом смысле классические SMP-компьютеры обладают архитектурой UMA (Uniform Memory Access). При этом применяется механизм (обычно аппаратного уровня – что быстрее), позволяющий пользовательским программам рассматривать всю (физически) распределенную между процессорами память как единое адресное пространство. Примерами NUMA-компьютеров является построенная еще в семидесятых годах и содержащая объединенный межкластерной шиной набор кластеров система Cm и объединяющий 256 процессоров комплекс BBN Butterfly (1981, фирма BBN Advanced Computers).

2.2 Распределение вычислений и данных в многопроцессорных вычислительных системах с распределенной памятью

В случае наличия в составе многопроцессорной вычислительной системы вычислительных узлов с локальной оперативной памятью кроме распределения частей вычисления по отдельным вычислительным узлам важно рациональным образом распределить по имеющимся вычислительным узлам данные (например, блоки обрабатываемых матриц значительной размерности). Дело в том, что затраты времени на обмен данными между обрабатывающими эти данные вычислительные узлы и вычислительными узлами, хранящими эти данные в своей локальной оперативной памяти, может на порядки замедлить процесс вычислений.

Ясно, что расположение большого пула данных на одном вычислительном узле вряд ли целесообразно вследствие неизбежной значительной потери времени на организацию пересылок отдельных блоков этих данным обрабатывающим вычислительным узлом. С другой стороны, чисто формальное разбиение данных на равное числу вычислительного узла число блоков чревато тем же.

Рациональное распределение данных по локальным оперативной памяти вычислительного узла должно совершаться с учетом частоты обращения каждого вычислительного узла к каждому блоку данных, расположенных на соответствующих вычислительных узлах при стремлении к минимизации числа обменов, что требует определения тонкой информационной структуры алгоритма.

Казалось бы, в общем случае возможно построение некоей функции трудоемкости (например, в смысле времени) вычислений, учитывающей как ресурсные затраты на собственно вычисления так и трудоемкость обменов при заданном распределении данных по вычислительным узлам и дальнейшей минимизации этой функции по параметру (параметрам) распределения данных; причем само распределение может являться изменяемым. Реально построение подобной функции затруднено вследствие необходимости количественного определения временных параметров выполнения операций и выявлении значимых параметров оптимизации. Претендентом на роль подобной функции может служить, например, вышеописанный сетевой закон Амдаля.

В стандартных пакетах решения задач линейной алгебры используются основанные на теоретическом анализе и долговременной практике методы распределения данных по вычислительным узлам.

2.3 Классификация параллельных вычислительных систем

Классификация архитектур вычислительных систем преследует цели выявление как основных факторов, характеризующих каждую архитектуру, так и взаимосвязей параллельных вычислительных структур.

SISD (Single Instruction stream / Single Data stream) – одиночный поток команд и одиночный поток данных; к SISD-классу относятся классические последовательные (фон-Неймановского типа) машины. В таких машинах имеется только один поток (последовательно обрабатываемых) команд, каждая из которых инициирует одну скалярную операцию. В этот класс попадают и машины с технологией конвейерной обработки.

SIMD (Single Instruction stream / Multiple Data stream) – одиночный поток команд наряду со множественным потоком данных. При этом сохраняется один поток команд, но включающий векторные команды, выполняющие одну арифметическую операцию сразу над многими данными. Выполнение векторных операций может производиться матрицей процессоров (как в машине ILLIAC IV) или конвейерным способом (Cray-1). Фактически микропроцессоры Pentium VI и Xeon c набором инструкций MMX, SSE, SSE2 являются однокристальными SIMD-системами.

Из стран СНГ SIMD-систем следует назвать ПС-2000 (1972 – 1975) – высокопараллельная компьютерная система для обработки информации с производительностью до 200 млн. оп/с.

MISD (Multiple Instruction stream/Single Data stream) – множественный поток команд и одиночный поток данных. Архитектура подразумевает наличие многих процессоров, обрабатывающих один и тот же поток данных; считается, что таких машин не существует.

MIMD (Multiple Instruction stream / Multiple Data stream) – множественные потоки как команд, так и данных. К классу MIMD принадлежат машины двух типов: с управлением от потока команд и управлением от потока данных; если в компьютерах первого типа используется традиционное выполнение команд последовательно их расположения в программе, то второй тип предполагает активацию операторов по мере их текущей готовности.

Класс предполагает наличие нескольких объединенных в единый комплекс процессоров, работающий каждый со своим потоком команд и данных.

Классический пример – система Denelcor HEP (Heterogeneous Element Processor); содержит до 16 процессорных модулей, через многокаскадный переключатель связанных со 128 модулями памяти данных, причем все процессорные модули могут работать независимо друг от друга со своими потоками команд, а каждый процессорный модуль может поддерживать до 50 потоков команд пользователей.

2.4 Многопроцессорные вычислительные системы с распределенной памятью

С последнего десятилетия 20 века наблюдается тенденция к монополизации архитектур супер-ЭВМ системами с распределенной памятью, причем в качестве процессоров на вычислительных узлах все чаще применяются легкодоступные готовые устройства. Основными преимуществами таких систем является огромная масштабируемость (в зависимости от класса решаемых задач и бюджета пользователь может заказать систему с числом узлов от нескольких десятков до тысяч); что привело к появлению нового названия для рассматриваемых систем – массивно-параллельные компьютеры (вычислительные системы архитектуры MPP – Massively Parallel Processing).

Первый суперкомпьютер с массивной параллельной обработкой – Connection Machine (СМ-1), была оснащена 64000 процессоров, каждый из который имел собственную память. СМ-1 выполняла сканирование 16 тыс. статей со сводками последних новостей за 1/20 сек. и разработала интегральную схему процессора с 4 тыс. транзисторов за три минуты. Выпуклыми представителями MPP-систем являются суперкомпьютеры серии Cry T3.

Cry T3E (1350) это мультипроцессорная вычислительная система 2000 года выпуска, с распределенной памятью построена из RISC-процессоров. Топология коммуникационной сети – трехмерный тор. Операционная система UNICOS/mk (операционная система UNIX с микроядром). Трансляторы для языков FORTRAN, HPF, C/C++. Тактовая частота 675 МГц. Количество процессоров от 40 до 2176. Максимальный объем оперативной памяти для каждого узла 512 Мбайт и максимальное быстродействие 2938 Гфлоп/с. В отличие от предшественника – Cry T3D, данной системе не требуется фронтальный компьютер.

В системе используется процессор Alpha21164A, однако, при необходимости, его несложно заменить другим, например, более быстродействующим процессором. Каждый процессорный элемент содержит центральный процессор, модуль памяти и коммуникационный узел для связи с другими процессорами. Пропускная способность канала связи между процессорами 325 Мбайт/с.

Поддерживаются модели программирования MPI, PVM, HPF, собственная библиотека обмена сообщениями Cray shmem. Быстродействие, полученное при решении систем линейных алгебраических уравнений, достигает 1,12 Тфлоп/с.

МРР – система состоит из однородных вычислительных узлов, включающих:

           - один, а иногда несколько центральных процессоров (обычно архитектуры RISC – Reduced Instruction Set Computing, для которой характерно длинное командное слово для задания операций, сокращенный набор команд и выполнение большинства операций за один такт процессора),

           - локальную память (причем прямой доступ к памяти других узлов невозможен),

           - коммуникационный процессор (или сетевой адаптер),

           - жесткие диски (необязательно) и/или другие устройства ввода/вывода.

К системе добавляются специальные узлы ввода-вывода и управляющие узлы. Вычислительные узлы связаны некоторой коммуникационной средой (высокоскоростная сеть, коммутаторы и т.п.).

Техническое обслуживание многопроцессорных систем является непростой задачей – при числе вычислительных узлов сотни/тысячи неизбежен ежедневный отказ нескольких из них; система 5k управления ресурсами (программно-аппаратный комплекс) массивно-параллельного компьютера обязана обрабатывать подобные ситуации в обход катастрофического общего рестарта с потерей контекста исполняющихся в данный момент задач.

2.4.1 Массивно-параллельные суперкомпьютеры серии CRY T3

Основанная в 1972 году фирма Cry Research Inc. (сейчас Cry Inc.), прославившаяся разработкой векторного суперкомпьютера Cry 1, в 1993 – 1995 годы выпустила модели Cry T3D/T3E, полностью реализующие принцип систем с массовым параллелизмом (систем MPP-архитектуры). В максимальной конфигурации эти компьютеры объединяют 32 – 2048 процессоров DEC Alpha 21064/150 MHz, 21164/600 MHz, 21164A/675 MHz (в зависимости от модели), вся предварительная обработка и подготовка программ (например, компиляция) выполняется на управляющей машине (хост-компьютере).

Разработчики серии Cry T3D/T3E пошли по пути создания виртуальной общей памяти. Каждый процессор может обращаться напрямую только к своей локальной памяти, но все узлы используют единое адресное пространство. При попытке обращения по принадлежащему локальной памяти другого процессора адресу генерируется специализированное аппаратное прерывание и операционная система выполняет пересылку страницы с одного узла на другой, причем вследствие чрезвычайно высокого быстродействия коммуникационной системы (пиковая скорость передачи данных между двумя узлами достигает 480 Мбайт/с) этот подход в целом оправдан. Однако замечен резко снижающий производительность эффект "пинг-понга" в случае попадания на одну страницу переменных, модифицируемых несколькими процессорами, эта страница непрерывно мигрирует между узлами. Вычислительные узлы выполняют программы пользователя в монопольном режиме (однозадачный режим).

Конкретное исполнение компьютеров серии Cry T3 характеризуется тройкой чисел, например, 24/16/576 (управляющие узлы/узлы операционной системы/вычислительные узлы); при используемой топологии "трехмерный тор" каждый узел (независимо от его расположения) имеет шесть непосредственных соседей. При выборе маршрута между двумя узлами А и В (3D-координаты которых суть рисунок 11) сетевые машрутизаторы, начиная процесс с начальной вершины А, сначала выполняют смещение по координате X таким образом, пока координаты очередного узла связи и узла B не станут равными; затем аналогичные действия выполняются по координате Y и далее по Z (физически подобная маршрутизация происходит одновременно по всем трем координатам). Смещения могут быть и отрицательными, при отказе одной или нескольких связей возможен их обход.

Другой интересной особенностью архитектуры Cry T3 является поддержка барьерной синхронизации – аппаратная организация ожидания всеми процессами определенной точки в программе, при достижении которой возможна дальнейшая работа. Компьютеры серии T3E демонстрировали производительность 1,8 – 2,5 Тфлопс (на 2048 микропроцессорах Alpha/600 MHz).

Дальнейшим развитием линии массивно-параллельных компьютеров Cry T3 является суперкомпьютер Cry XT3. Каждый вычислительный узел Cry XT3 включает процессор AMD Opteron, локальную память (1 – 8 Гбайт) и обеспечивающий связь по коммуникационному блоку Cry SeaStar канал Hyper Transport, имеющий пиковую производительность (для AMD Opteron 2,4 GHz) от 2,6 Тфлопс (548 процессоров, оперативная память 4,3 Тбайт, топология 6×12×8) до 147 Тфлопс. Cray XT3 работает под управлением операционной системы UNICOS/lc, позволяющей объединять до 30000 вычислительных узлов, применяются компиляторы Fortran 77/90/95 и C/C++, коммуникационные библиотеки MPI (Message Passing Interface c поддержкой стандарта MPI 2.0) и ShMem (разработанная Cray Research Inc. библиотека для работы с общей памятью), стандартные библиотеки численных расчетов.

Несмотря на достигнутые столь высокие результаты в области MPP-систем фирма Cry Inc. производит векторно-конвейерный компьютеры, причем эти модели могут быть объединены в MPP-систему. Производительность каждого процессора компьютера Cry SV1 достигает 4 Гфлопс (общая пиковая производительность системы 32 Гфлопс), общее число процессоров может достигать 1000.

Рисунок 11. Коммуникационная решетка "трехмерный тор" компьютера Cray T3E

2.4.2 Кластерные системы класса BEOWULF

Запредельная стоимость промышленных массивно-параллельных компьютеров не давали покоя специалистам, желающим применить в своих исследованиях вычислительные системы сравнимой мощности, но не имеющих возможностей приобрести промышленные супер-ЭВМ. Поиски в этом направлении привели к развитию вычислительных кластеров (не путать с кластерами баз данных и WEB-серверов); технологической основой развития кластеризации стали широкодоступные и относительно недорогие микропроцессоры и коммуникационные (сетевые) технологии, появившиеся в свободной продаже в девяностых годах.

Вычислительный кластер представляет собой совокупность вычислительных узлов (от десятков до десятков тысяч), объединенных высокоскоростной сетью c целью решения единой вычислительной задачи. Каждый узел вычислительного кластера представляет собой фактически программируемых электронно-вычислительных машин (часто двух- или четырех- процессорный/ядерный SMP-сервер), работающую со своей собственной операционной системой (в подавляющем большинстве Linux(*)); объединяющую сеть выбирают исходя из требуемого класса решаемых задач и финансовых возможностей, практически всегда реализуется возможность удаленного доступа на кластер посредством InterNet.

Вычислительные узлы и управляющий компьютер обычно объединяют (минимум) две (независимые) сети сеть управления (служит целям управления вычислительными узлами) и (часто более производительная) коммуникационная сеть (непосредственный обмен данными между исполняемыми на узлах процессами), дополнительно управляющий узел имеет выход в Internet для доступа к ресурсам кластера удаленных пользователей, файл-сервер выполняет функции хранения программ пользователя (рисунок 12). Администрирование кластера осуществляется с управляющей ЭВМ (или посредством удаленного доступа), пользователи имеют право доступа (в соответствие с присвоенными администратором правами) к ресурсам кластера исключительно через управляющий компьютер.

Windows-кластеры значительной мощности до настоящего времени остаются экзотикой в силу известных причин (несмотря на активно продвигаемые MS решения класса Windows Compute Cluster Server – WCCS).

Одним из первых кластерных проектов явился проект BEOWULF. Проект "БЕОВУЛЬФ" был заложен в созданном на основе принадлежащей NASA организации GSFC (Goddard Space Flight Center) исследовательском центре CESDIS (Center of Excellence in Space Data and Information Sciences) в 1994 году и стартовал сборкой в GSFC 16шестнадцатиузлового кластера (на процессорах 486DX4/100 MHz, 16 Mb памяти, 3 сетевых адаптера на каждом узле и 3 параллельных 10 Mbit Ethernet-кабелей); вычислительная система предназначалась для проведения работ по проекту ESS (Earth and Space Sciences Project).

Позднее в подразделениях NASA были собраны другие модели BEOWULF-подобных кластеров: например, theHIVE (Highly-parallel Integrated Virtual Environment) из 64 двухпроцессорных (Pentium Pro/200 MHz, 4 Gb памяти и 5 коммутаторов Fast Ethernet в каждом) узлов. Именно в рамках проекта Beowulf были разработаны драйверы для реализации режима Channel Bonding.

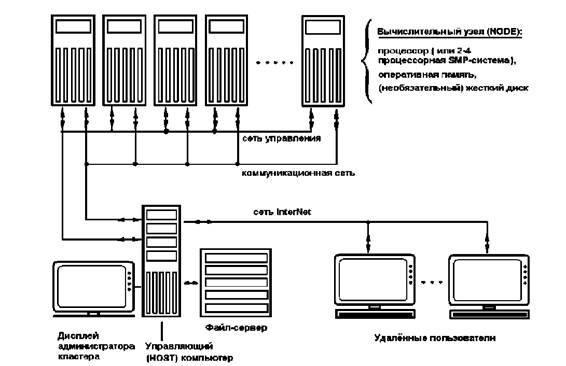
Рисунок 12. Укрупненная схема вычислительного кластера

"Беовульф" типичный образец многопроцессорной системы MIMD (Multiple Instruction − Multiple Data), при этом одновременно выполняются несколько программных ветвей, в определенные промежутки времени обменивающиеся данными. Многие последующие разработки во всех странах мира фактически являются кланами Beowulf.

В 1998 году в национальной лаборатории Лос-Аламос астрофизик Michael Warren с сотрудниками группы теоретической астрофизики построили вычислительную систему Avalon, представляющую Linux-кластер на процессорах DEC Alpha/533 MHz. Первоначально Avalon состоял из 68 процессоров, затем был расширен до 140, в каждом узле установлено 256 MB оперативной памяти, EIDE-жесткий диск 3,2 Gb, сетевой адаптер фирмы Kingston.

Узлы соединены с помощью четырех коммутаторов Fast Ethernet и центрального двенадцатипортового коммутатора Gigabit Ethernet фирмы 3Com.

Типичным образцом массивно-параллельной кластерной вычислительной системы являются МВС-1000M (коммуникационная сеть – Myrinet 2000, скорость обмена информацией 120–170 Мбайт/сек, вспомогательные – Fast и Gigabit Ethernet) и МВС-15000ВС.

Требование максимальной эффективности использования ресурсов вычислительных мощностей (как процессорных, так и оперативной и дисковой памяти) отдельных процессоров кластера неизбежно приводит к снижению "интеллектуальности" операционной системы вычислительных узлов до уровня мониторов; с другой стороны, предлагаются распределенные кластерные операционные системы – например, Amoeba, Chorus, Mach и др.

Специально для комплектации аппаратной части вычислительных кластеров выпускаются Bladed - сервера (*) – узкие вертикальные платы, включающие процессор, оперативную память (обычно 256 – 512 МБайт при L2-кэше 128 – 256 КБайт), дисковую память и микросхемы сетевой поддержки; эти платы устанавливаются в стандартные "корзины" формата 3U шириной 19² и высотой 5,25² до 24 штук на каждую (240 вычислительных узлов на стойку высотою 180 см). Для снижения общего энергопотребления могут применяться расходующие всего единицы ватт (против 75 W для P4 или 130 W для кристаллов архитектуры IA-64) процессоры Transmeta Crusoe серии TM 5x00 с технологией VLIW; при этом суммарная потребляемая мощность при 240 вычислительных узлах не превышает 1 кВт.

2.4.3 Коммуникационные технологии, используемые при создании массово-параллельных суперкомпьютеров

Важным компонентом массово-параллельных компьютеров является коммуникационная среда – набор аппаратных и программных средств, обеспечивающих обмен сообщениями между процессорами. Фактически коммуникационная среда в данном случае является аналогом общей шины традиционных электронно-вычислительных машин и посему оказывает сильнейшее влияние на производительность всей вычислительной системы.

Заключение

Параллельнoe программирование представляет собой целое направление смежных вопросов, включающих аппаратную поддержку, анализ структуры алгоритмов с целью выявления параллелизма и алгоритмические языки для программирования параллельных задач.

Технологии параллельных вычислений в настоящее время бурно развиваются в связи с требованиями мировой науки и технологий.

Достаточно часто приходится сталкиваться с такими задачами, которые, представляя немалую ценность для общества, не могут быть решены с помощью относительно медленных компьютеров офисного или домашнего класса. Единственная надежда в этом случае возлагается на компьютеры с большим быстродействием, которые принято называть суперкомпьютерами. Только машины такого класса могут справиться с обработкой больших объемов информации. Это могут быть, например, статистические данные или результаты метеорологических наблюдений, финансовая информация. Иногда скорость обработки имеет решающее значение. Это составление прогноза погоды и моделирование климатических изменений. Чем раньше предсказано стихийное бедствие, тем больше возможностей подготовиться к нему. Важной задачей является моделирование лекарственных средств, расшифровка генома человека, разведка месторождений нефти и газа и другие объемные задачи, решение которых возможно с помощью суперкомпьютеров и кластерных систем.

Сегодняшняя проблема – явный недостаток аппаратных средств для параллельных вычислений в учебных и научных учреждениях, что не дает возможности всестороннего освоения соответствующих технологий; часто практикуемое чисто теоретическое изучение предмета приводит скорее к негативным, чем к позитивным следствиям. Только сейчас появляются технологии, позволяющие ввести практику параллельных вычислений в большинство учебных и производственных лабораторий.

Создание эффективных параллельных программ требует намного более серьезного и углубленного анализа структуры алгоритмов, нежели при традиционно-последовательном программировании, причем некоторые подходы невозможно реализовать без серьезного изменения мышления программистов.

Наряду с теоретическим анализом для получения практически значимых результатов необходима постоянная практика в создании параллельных программ.

Список использованной литературы

1.         С. Немнюгин, О. Стесик. Параллельное программирование для многопроцессорных вычислительных систем

2.         Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. -СПб.: БХВ-Петербург, 2004. -608 с.

3.         Гарви М.Дейтел. Введение в операционные системы (пер. с англ. Л.А.Теплицкого, А.Б.Ходулева, Вс.С.Штаркмана под редакцией Вс.С. Штаркмана). -М.: Мир, 1987 (электронная версия http://www.deepweb.ru, 2004)

4.         Гергель В.П., Стронгин Р.Г. Основы параллельных вычислений для многопроцессорных вычислительных систем (учебное пособие, изд. 2, дополненное). -Н.Новгород.: изд. ННГУ им. Н.И.Лобачевского, -2003 (электронная версия http://pilger.mgapi.edu/metods/1441/basic_pr.zip).

5.         Корнеев В.В. Вычислительные системы. -М.: Гелиос АРВ, -2004, -512 с.

6.         Лацис А.О. Как построить и использовать суперкомпьютер. -М.: Бестселлер, 2003.-240 с.

7.         Крюков В.А.. Разработка параллельных программ для вычислительных кластеров и сетей. // Информационные технологии и вычислительные системы. -М.: № U2,2003.

8.         Шпаковский Г.И. Организация параллельных ЭВМ и суперскалярных процессоров. // Учеб. пособие. -Минск.: Белгосуниверситет, 1996. -296 с. (электронная версия http://pilger.mgapi.edu/metods/1441/spakovsk.zip)

9.         Шпаковский Г.И., Серикова Н.В. Программирование для многопроцессорных систем в стандарте MPI. -Минск:, БГУ, 2002. -325 с. (электронная версия http://www.cluster.bsu.by/download/book_PDF.pdf, http://pilger.mgapi.edu/metods/1441/pos_mpi.pdf)

10.      Андрианов А.Н., Бугеря А.Б., Ефимкин К.Н., Задыхайло И.Б. Норма. Описание языка. Рабочий стандарт. //Препринт ИПМ им.М.В.Келдыша РАН, № 120, 1995, -50 с.8.

11.      Информационно-аналитические материалы по параллельным вычислениям (электронная версия http://parallel.ru